HAVO WB, 2016 - I  PILOT

 

De rechte van Euler.
       

Gegeven is cirkel c met middelpunt  M(1/2,  1/2), die door het punt A(0, 4) gaat.
       

3p.

1.

 Stel een vergelijking op van c.
       

De punten B(−3, 0) en C(4, 0) liggen op c.
Punt Q is het midden van lijnstuk AC.
Lijn k is de lijn door B en Q. Een vergelijking van k is y = 2/5x + 6/5.
Punt P is het midden van lijnstuk AB.
Lijn l is de lijn door C en P.
Punt S is het snijpunt van k en l.
Zie de figuur.
       

       

De coördinaten van S zijn (1/3, 4/3)
       

5p.

2.

Bewijs dat de coördinaten van S inderdaad (1/3, 4/3) zijn.
       

Lijn n gaat door C en staat loodrecht op AB. Bovendien snijdt lijn n de y-as in punt T.
Zie onderstaande figuur.
       

       

Volgens de achttiende-eeuwse wiskundige Euler liggen de punten M, S en T op één lijn.
       

7p.

3.

 Bewijs dat M, S en T inderdaad op één lijn liggen.
       
Een wortelfunctie.
       

De functie f  is gegeven door f (x) = √(−3x + 6) .  Lijn k heeft vergelijking   y = -7/4 • x + 7/2  
In onderstaande figuur zie je de grafiek van f en lijn k.
       

       
Lijn k en de grafiek van f hebben twee punten gemeenschappelijk.
       

5p.

4.

 Bereken exact de x-coördinaten van deze twee punten.
     

 

De verticale lijn met vergelijking x = p snijdt k in punt A en de grafiek van f in punt B. De y-coördinaat van B is groter dan de y-coördinaat van A.
Zie de volgende figuur.
       

       

Er is een waarde van p waarvoor de afstand tussen A en B maximaal is.
       

6p.

5.

 Bereken met behulp van differentiëren deze waarde van p.
     

 
Schijngestalten van de maan.
       

Van de maan is ook bij een wolkeloze hemel niet altijd een even groot gedeelte zichtbaar. Het percentage van de maan dat zichtbaar is, verloopt bij benadering periodiek. Voor het jaar 2017 is dit percentage in Nederland te benaderen met de formule:

P = 50 + 50sin (0,212769t - 1,042563)

Hierin is P het percentage van de maan dat zichtbaar is en t is de tijd in dagen met t = 0 op 1 januari 2017 om 0:00 uur.
       

3p.

6.

 Bereken de periode van P in hele minuten nauwkeurig.
     

 

De vorm van het zichtbare gedeelte van de maan wordt de schijngestalte van de maan genoemd. Vier speciale schijngestalten zijn nieuwe maan, eerste kwartier, volle maan en laatste kwartier. Zie de figuur, waarin ze op volgorde staan afgebeeld, elk met het bijbehorende percentage van de maan dat zichtbaar is.
       

       

De volgorde waarin deze schijngestalten voorkomen, is dus altijd: eerst nieuwe maan, dan eerste kwartier, dan volle maan en daarna laatste kwartier. Daarna volgt opnieuw nieuwe maan, enzovoort.
       

3p.

7.

Bereken met behulp van de formule voor P op welke datum in 2017 het voor het eerst nieuwe maan zal zijn.
     

 

4p.

8.

Onderzoek met behulp van de formule voor P tussen welke twee opeenvolgende schijngestalten de maan zich op 22 februari 2017 zal bevinden
     

 
Gebroken functie en raaklijn.
       

De functie f is gegeven door    f (x) = 12/(x - 3) + 4.
Lijn l raakt in de oorsprong aan de grafiek van f . Zie de figuur.
       

       
De richtingscoëfficiënt van l is -4/3.
       

3p.

9.

Toon met behulp van differentiëren aan dat de richtingscoëfficiënt van l inderdaad -4/3 is.
     

 

Lijn k staat loodrecht op l en gaat door de oorsprong. k snijdt de grafiek van f in de oorsprong, en ook nog in een ander punt.
       

6p.

10.

 Bereken exact de coördinaten van dit punt.
     

  
Klok.
       

       

De klok op de foto hierboven heeft een kleine wijzer met een lengte van 8,5 cm en een grote wijzer met een lengte van 12,5 cm. Het uiteinde van de kleine wijzer noemen we A; het uiteinde van de grote wijzer noemen we B.

Als het bijvoorbeeld 2:00 uur is, dan wijst de kleine wijzer precies naar 2 en staat de grote wijzer precies op 12. Is het bijvoorbeeld 2:15 uur (kwart over twee), dan heeft de kleine wijzer precies een kwart van de hoek tussen de 2 en de 3 afgelegd; de grote wijzer staat dan precies op 3.

Op de klok op de foto is het precies 2:25 uur (vijf voor half drie).
       

7p.

11.

Bereken in deze situatie de afstand tussen A en B. Geef je antwoord in gehele millimeters nauwkeurig..
       
Karpers.
       

In het begin van hun leven ontwikkelen karpers zich van larve tot klein visje. Aan het einde van deze ontwikkeling heeft het visje een lengte van ongeveer 1,9 cm.

De lengte van de karperlarve in centimeter noemen we L.
Het gewicht van de karperlarve in gram noemen we G.
In de figuur is het verband tussen log(L) en log(G) weergegeven.
       

       

4p.

12.

Bepaal met behulp van de figuur het gewicht van een karperlarve met een lengte van 0,8 cm. Geef je antwoord in hele milligrammen nauwkeurig.
     

 

Het verband tussen de lengte van karperlarven en hun gewicht kan beschreven worden met een formule van de vorm:

G = 0,014 • Lb   met 0,2 ≤ L ≤ 1,9

Hierin is L de lengte in centimeter, G het gewicht in gram en b een constante.

Een karperlarve van 1,9 cm weegt ongeveer 0,25 g.
Hieruit volgt dat b afgerond op één decimaal gelijk is aan 4,5.
     

 

3p.

13.

Bereken b met behulp van deze gegevens in twee decimalen nauwkeurig.
       

De formule G = 0,014 • L4,5 is te herleiden tot een formule van de vorm log(G) = p + q • log(L) .
       

4p.

14.

Bereken de waarden van p en q. Geef beide waarden in één decimaal nauwkeurig.
       

Voor volwassen karpers (met 10 ≤ L ≤ 94) is G evenredig met L3,13 .

Hierin is L weer de lengte in centimeter en G het gewicht in gram.
       

3p.

15.

Bereken hoeveel keer zo zwaar een volwassen karper van 94 cm is in vergelijking met een volwassen karper van 10 cm. Rond je antwoord af op honderdtallen.
     

 
Exponentiële functie.
       
De functie f  is gegeven door   f (x) = 3x −1  − 2 . Zie de figuur.
       

       

3p.

16.

 Bereken exact de waarde van x waarvoor geldt:   f (x) = 241
       

De functie g is gegeven door g(x) = 3x.

Op de grafiek van g worden de volgende transformaties uitgevoerd: eerst de verschuiving 6 omlaag, gevolgd door de vermenigvuldiging met  1/3 ten opzichte van de x-as. Op deze manier ontstaat de grafiek van de functie h.
       

4p.

17.

 Toon op algebraïsche wijze aan dat h dezelfde functie is als f.
     

 

De grafiek van g wordt met a vermenigvuldigd ten opzichte van de y-as.
Hierdoor ontstaat de grafiek van de functie k. Het punt P(−20, 81) ligt op de grafiek van k. Zie onderstaande figuur.
       

       

4p.

18.

 Bereken exact de waarde van a.
     

  

 

UITWERKING
   
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
1. M = (1/2,  1/2), dus de vergelijking is  (x - 1/2)2 + (y - 1/2)2 = r2
A(0, 4)  invullen:   (-1/2)2 + (31/2)2  = r2 = 12,5
(x - 1/2)2 + (y - 1/2)2 = 121/2
   
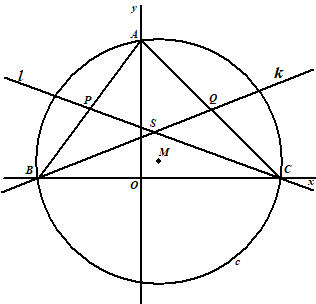
2. A = (0, 4) en  B = (-3, 0) en  C = (4,0)

P is het midden van AB dus P = (-11/2, 2)
CP heeft helling  (0 - 2)/(4 - - 1,5) = -2/5,5 = -4/11 dus is de lijn   y = -4/11x + b
C ligt erop dus 0 = -4/11 • 4 + b  dus  b = 16/11
CP is de lijn  y = -4/11x + 16/11 

Q is het midden van AC  dus  Q = (2, 2)
BQ heeft helling  (0 - 2)/(-3 - 2) = -2/-5 = 2/5  dus is de lijn  y = 2/5x + b
Q ligt erop dus  2 = 2/5 • 2 + b dus b = 6/5
BQ is de lijn  y = 2/5x + 6/5

BQ en CP snijden:
-4/11x + 16/11   = 2/5x + 6/5
16/11 - 6/5  = 2/5x + 4/11x
14/55 = 42/55x
14 = 42x
x = 1/3
dan is y = 2/5 • 1/3 + 6/5 = 4/3
   
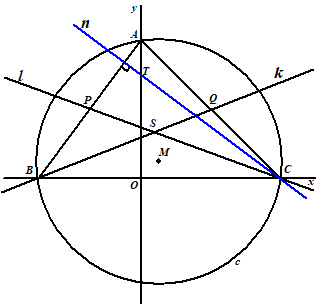
3. AB heeft helling (0 - 4)/(-3 - 0) = 4/3  dus  n heeft helling -3/4 en is de lijn  y = -3/4x + b
Punt C ligt erop, dus  0 = -3/4 • 4 + b dus b = 3
Lijn n  snijdt de y-as in het punt T(0, 3)

T = (0, 3),  M = (1/2, 1/2) en  S = (1/3, 4/3)

MT heeft helling  (0,5 - 3)/(0,5 - 0) = -2,5/0,5 = -5
ST heeft helling  (4/3 - 3)/(1/3 - 0) = -5/3/1/3 = -5
De hellingen zijn gelijk, dus M, S en T liggen op één lijn. 
   
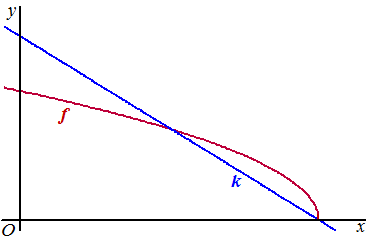
4. √(-3x + 6) = -7/4x + 7/2
vermenigvuldig met 4:   4√(-3x + 6) = -7x + 14
kwadrateren:  16(-3x + 6) = (-7x + 14)2
-48x + 96 = 49x2 - 196x + 196
0 = 49x2 -148x + 100
ABC-formule:    x = (148 ±√2304)/98  ⇒  x =  2  of  x = 50/49
   
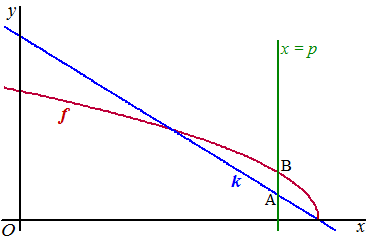
5. De afstand tussen A en B is   L =  yB - yA = (√(-3x + 6) - (7/4x + 7/2)  = (-3x + 6)0,5 - 7/4x - 7/2
Dat is minimaal als de afgeleide ervan nul is:
L' = 0,5 • (-3x + 6)-0,5 • -3  - 7/4  = 0    (die -3 komt natuurlijk van de kettingregel)
0,5 • (-3x + 6)-0,5 • -3 = 7/4
1,5 • (-3x + 6)-0,5 = 7/4
(-3x + 6)-0,5 =  7/6
(-3x + 6)0,5 = 6/7
-3x + 6 = 36/49
-3x = -258/49
x = 86/49  ≈ 1,755...
   
6. de periode is  2π/0,212769 = 29,53054866... dagen
Een dag is 24 • 69 = 1440 minuten
Dat is dus 29,53.... 1440 = 42524 minuten 
   
7. P = 0 geeft  0 = 50 + 50sin(blablabla)
Dus  sin(blablabla) = -1
0,212769t - 1,042563  = 1,5π + k2π 
0,212769t =  5,754952 + k2π
t =  27,04789 + k • 29,53 

Dat is voor het eerst op 28 januari 2017 
   
8. 22 februari  ligt tussen t = 52 en t = 53
Dan is  (invullen)  P = 22 en  P = 14
Dat is dus tussen nieuwe maan en eerste kwartier OF tussen laatste kwartier en nieuwe maan.
Maar omdat P van t = 52 naar t = 53 afgenomen is (van 22 naar 14)  is het tussen laatste kwartier en nieuwe maan.
   
9. f(x) =  12(x - 3)-1 + 4
f '(x) = -1 • 12 • (x - 3)-2
f '(0) = -12 • (-3)-2 = -12 • 1/3² = -12/9 = -4/3
   
10. l heeft helling  -4/3  dus k heeft helling  3/4  en is dus de lijn   y =3/4x
3/4x = 12/(x - 3) + 4
vermenigvuldig met 4:   3x = 48/(x - 3) + 16
vermenigvuldig met (x - 3):   3x(x - 3) = 48 + 16(x - 3)
3x2 - 9x = 48 + 16x -48
3x2 - 25x = 0
x(3x - 25) = 0
x = 0  ∨  x = 25/3
x = 25/3  geeft  y = 3/4 • 25/3 = 25/4
Het snijpunt is  (25/3, 25/4)
   
11. de hoek tussen twee uren is 360/12 =  30º

sinds 14:00 uur is er 25/60 uur verstreken dus heeft de kleine wijzer 25/60 • 30º = 12,5º gedraaid dus maakt nu een hoek van  60 + 12,5 = 72,5º met 12 uur.

de grote wijzer maakt een hoek van 5 • 30 = 150º met twaalf uur
De hoek tussen de wijzers is dus  150 - 72,5 = 77,5º

cosinusregel:  AB2 = 8,52 + 12,52 - 2 • 8,5 • 12,5 • cos(77,5)
AB2 = 182,51
AB = √182,51 = 13,5 cm = 135 mm
   
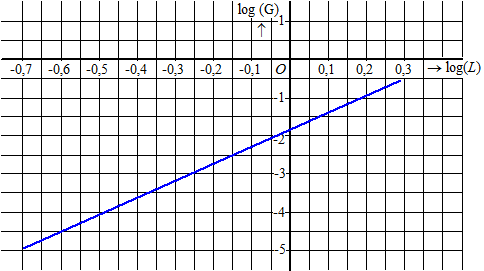
12. log(0,8) = -0,09
aflezen:  log(L) = -0,09  geeft  log(G) = -2,3
G = 10-2,3 = 0,005  dus dat is 5 mg
   
13. 0,25 = 0,014 • 1,9b
17,857... = 1,9b
b = log(17,857...)/log(1,9) ≈ 4,49
   
14. G = 0,014 • L4,5 
log(G) = log(0,014 • L4,5)
log(G) = log(0,014) + log(L4,5)
log(G) = -1,85 + 4,5log(L)
dus p = -1,9 en q = 4,5
   
15. Evenredig betekent dat  G = a • L3,13
L = 10  geeft  G = a • 103,13 = 1349 • a
L = 94 geeft  G = a • 943,13 = 1499306 • a
De verhouding is 1499306/1349 = 1111
Afgerond op honderdtallen is dat 1100 keer zo zwaar.
   
16. 3x - 1 - 2 = 241
3x - 1 = 243
x - 1 = 5
x = 6
   
17. 3x  verschuiving 6 omlaag geeft  3x - 6
3x - 6 vermenigvuldiging met 1/3 tov x-as  geeft   1/3(3x - 6)
1/3(3x - 6) = 1/3 • 3x  -  2  =  3-1 • 3x - 2 = 3-1+x - 2  en dat is inderdaad f.
   
18. y = 3x  vermenigvuldigen met factor a tov y-as  geeft  y = 3x/a 
(-20, 81) ligt daarop dus  81 = 3-20/a 
-20/a = 4
a = -5