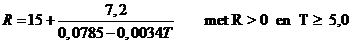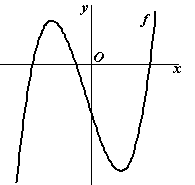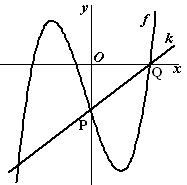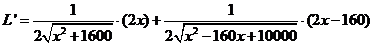HAVO WB, 2011 - I

 

Overlevingstijd.
       

Als iemand in koud water terecht komt, daalt zijn lichaamstemperatuur. Als de lichaamstemperatuur is gedaald tot 30 ºC ontstaat een levensbedreigende situatie. De tijd die verstrijkt tussen het te water raken en het bereiken van een lichaamstemperatuur van 30 ºC wordt de overlevingstijd genoemd.

Bij de eerste drie vragen wordt uitgegaan van een persoon die te water is geraakt in gewone kleding en met een reddingsvest. Voor deze persoon geldt de volgende formule:
       

       

Hierin is R de overlevingstijd in minuten en T de watertemperatuur in ºC.

Bij een watertemperatuur van 20 ºC is de overlevingstijd groter dan bij een watertemperatuur van 10 ºC.
       
3p. 1. Bereken hoeveel keer zo groot.  
       
5p. 2.

Bereken op algebraïsche wijze de watertemperatuur waarbij de overlevingstijd 5,0 uur is. Rond daarna je antwoord af op een geheel aantal graden.
     

 

In de figuur is de grafiek van R als functie van T  geschetst. De grafiek heeft een verticale asymptoot.

     
3p. 3.

Bereken de waarde van T die bij de verticale asymptoot hoort en leg uit wat de betekenis van de verticale asymptoot is voor de situatie van de te water geraakte persoon.
     

 

De overlevingstijd van personen die te water raken, is niet alleen afhankelijk van de watertemperatuur. De kleding die een persoon draagt, is ook van invloed op de overlevingstijd.
In de volgende tabel staan watertemperaturen met bijbehorende overlevingstijden voor personen in zwemkleding.
       
watertemperatuur T in ºC 5,0 10 15 20
overlevingstijd Z in uren 0,5 1,0 2,0 4,0
       

We gaan voor 5,0 ≤ T ≤ 20 uit van een exponentieel verband tussen T en Z.

Iemand ligt in zwemkleding in water van 17 ºC.
       
3p. 4.

Bereken op algebraïsche wijze zijn overlevingstijd. Geef je antwoord in uren. Rond hierbij af op één decimaal.
     

 
Polynoom
       

De functie f is gegeven door f (x) = (x + 1)(x2 - 16).  Van één van de twee toppen van de grafiek van f is de x-coördinaat positief. Zie de volgende figuur.
       

       
5p. 5. Bereken op algebraïsche wijze de coördinaten van deze top.  
     

 

Punt P is het snijpunt van de grafiek van f met de y-as. Punt Q is het snijpunt van de grafiek van f met de positieve x-as. Lijn k gaat door de punten P en Q. Zie onderstaande figuur.
       

       
5p. 6. Stel op algebraïsche wijze een vergelijking op van k.  
     

 

 

Lichaam in kubus
       

Gegeven is de kubus ABCD.EFGH met ribbe 6,0 cm. Binnen deze kubus bevindt zich het lichaam ABCD.MGH. Het punt M ligt in het bovenvlak van de kubus. De afstand van M tot GH is 4,0 cm en HM = GM . Zie de volgende figuur.
       

       
3p. 7.

Teken op ware grootte het bovenaanzicht van het lichaam ABCD.MGH. Zet de letters bij de hoekpunten.
     

 

In de volgende figuur  is een begin gemaakt met een uitslag van het lichaam ABCD.MGH op schaal 1:2.
       

       
7p. 8. Maak de uitslag af. Zet de letters bij de hoekpunten en licht je werkwijze toe.
     

 
Het lichaam ABCD.MGH kan worden gesplitst in twee delen: de piramide ABGH.M en het prisma ADH.BCG. De rechthoek ABGH is het grondvlak van de piramide ABGH.M. De hoogte van deze piramide is gelijk aan de lengte van het lijnstuk MQ in het zijaanzicht van het lichaam en de kubus in de figuur hiernaast.

     
6p. 9. Bereken op algebraïsche wijze de inhoud van het lichaam ABCD.MGH .
     

 
Bushalte
       

Langs een rechte weg staan twee flatgebouwen. De ingang van flat 1 (punt E) ligt 40 meter van de weg af en de ingang van flat 2 (punt D) ligt 60 meter van de weg af. Men wil een bushalte plaatsen (punt B) en daarna van de bushalte naar de ingang van elk van de twee flats een recht voetpad aanleggen. Punt A is het punt aan de weg dat het dichtst bij de ingang van flat 1 ligt en punt C is het punt aan de weg dat het dichtst bij de ingang van flat 2 ligt. De afstand tussen punt A en punt C is 80 meter. In de figuur hieronder is van deze situatie een schematisch bovenaanzicht getekend.
       

       

De lengte van het voetpad tussen de bushalte en de ingang van flat 1 in meters wordt gegeven door de formule BE = √(x2 + 1600) en de lengte van het voetpad tussen de bushalte en flat 2 in meters wordt gegeven door de formule BD = √(x2 + 160x + 10000) . Hierin is x de afstand tussen punt A en de bushalte B in meters. Het is mogelijk de bushalte zo te plaatsen dat de twee voetpaden even lang zijn.
       
4p. 10. Bereken op algebraïsche wijze de waarde van x in deze situatie.
     

 

De totale lengte van de twee voetpaden L in meters wordt gegeven door de formule:
       

       
Als de twee voetpaden even lang zijn, is de totale lengte van deze voetpaden (ongeveer) 132 meter. Men wil de bushalte zo plaatsen dat de totale lengte van de twee voetpaden minimaal is. Hierdoor hoeft er minder dan 132 meter voetpad aangelegd te worden.
       
6p. 11. Bereken met behulp van differentiëren hoeveel meter minder.  
     

 
Sinusoïde
       

Van een sinusoïde zijn de punten (0, 0) en (1/2π ,1) twee opeenvolgende toppen. Zie de figuur.
       

       

Deze sinusoïde kan worden beschreven door een formule van de vorm y = a + b • sin(c(x - d)) .
       
4p. 12. Bepaal mogelijke waarden van a, b, c en d.  
     

 
Een andere formule die deze sinusoïde beschrijft, is  y = (sin x)2 .
       
4p. 13.

Bereken met behulp van deze formule op algebraïsche wijze de helling van de raaklijn aan de sinusoïde in het punt met x-coördinaat  1/4π .
     

 

 

Toiletpapier
       

Toiletpapier zit vaak op een rol. In deze opgave wordt een wiskundig model van een rol toiletpapier bekeken. In dit model is een rol toiletpapier een cilinder waaruit in het midden een cilinder is weggelaten. In figuur 1 is het model van een volle rol toiletpapier te zien. Deze rol heeft een buitendiameter van 12,0 cm, een binnendiameter van 4,0 cm en een hoogte van 10,0 cm.
       

       
Het volume van het toiletpapier op de rol in de rechter figuur is 320π cm3.
       
3p. 14. Toon dit aan.  
     

 

Iemand beweert dat de helft van het toiletpapier gebruikt is, wanneer de buitendiameter 8,0 cm is (midden tussen 4,0 cm en 12,0 cm). Dit is onjuist.
       
4p. 15.

Bereken de werkelijke buitendiameter van de toiletrol als de helft van het toiletpapier gebruikt is.
     

 

De rol toiletpapier bestaat uit een aantal velletjes. De buitendiameter van de rol toiletpapier hangt af van het aantal velletjes dat nog op de rol zit. Voor de rol waarvan het model in figuur 1 te zien is, geldt de formule:

Hierin is d de buitendiameter in cm en v het aantal velletjes toiletpapier dat nog op de rol zit.
Een volle rol heeft een buitendiameter van 12,0 cm. Een velletje toiletpapier is 13,6 cm lang.
       
4p. 16. Bereken hoeveel meter papier er op een volle rol zit.
     

 

       

Toiletpapier wordt vaak per vier rollen verpakt in plastic zoals te zien is op foto 2. Ga ervan uit dat het plastic nergens overlapt. In de rechter figuur  is een schematisch bovenaanzicht te zien met de plastic verpakking van vier rollen die elk de afmetingen van het model van het begin van deze opgave hebben.
       
4p. 17.

Bereken de oppervlakte van het plastic dat nodig is om de vier rollen op deze manier te verpakken. Geef je antwoord in cm2 nauwkeurig.
     

 
       

 

Logaritmentafel.
       

Wanneer de uitkomst van een logaritme geen geheel getal is, wordt de waarde vaak berekend met behulp van de rekenmachine. 50 jaar geleden waren er nauwelijks rekenmachines. De middelbare scholieren van toen gebruikten tabellenboekjes om de waarde van een logaritme te bepalen. Zie de foto. In de tabel staat een stukje uit zo’n tabellenboekje.
       

n log n
1 0
2 0,3010
3 0,4771
4 0,6021
5 0,6990
6 0,7782
7 0,8451
8 0,9031
9 0,9542
10 1
100 2
1000 3
       

Met behulp van de tabel en de rekenregels voor logaritmen is het mogelijk om logaritmische of exponentiële vergelijkingen op te lossen. Hierbij kan, zonder de log-toets van de (grafische) rekenmachine te gebruiken, een benadering van het antwoord gevonden worden.

Voorbeeld: log 11/2 = log3/2 = log3 - log2 ≈ 0,4771 - 0,3010 ≈ 0,176
       
3p. 18.

Bereken log 24 op algebraïsche wijze met behulp van de tabel, dus zonder gebruik te maken van de log-toets op je rekenmachine.
       

 
Gegeven is de vergelijking 7x = 25.
       
4p. 19.

Los deze vergelijking op algebraïsche wijze op met behulp van de tabel, dus zonder gebruik te maken van de log-toets op je rekenmachine. Rond je antwoord af op drie decimalen.
     

 

 

UITWERKING
   
1. R(20) = 15 + 7,2/(0,0785 - 0,0034 • 20) ≈ 177
R(10) = 15 + 7,2/(0,0785 - 0,0034 • 10) ≈ 701
Dat is dus  701/177 ≈ 4 keer zo groot
   
2. 5,0 uur is  5,0 • 60 = 300 minuten.
300 = 15 + 7,2/(0,0785-0,0034T)
⇒ 285 = 7,2/(0,0785-0,0034T)
⇒ 0,0785 - 0,0034T = 7,2/285 = 0,02526...
⇒ -0,0034T = -0,05323...
⇒ T = 15,66, dus ongeveer 16ºC
   
3. Er is een verticale asymptoot als de noemer van de breuk nul is, dus als  0,0785 - 0,0034T = 0
0,0034T = 0,0785  ⇒ T = 23 ºC
Als de temperatuur naar 23ºC nadert, dan wordt de overlevingstijd oneindig groot. Dat betekent dat de watertemperatuur dan meer levensbedreigend is, dus niet meer van invloed is.
   
4. De vermenigvuldigingsfactor in de tabel is steeds 2, maar dat is per 5ºC
Per graad geldt dan  g5 = 2  ⇒  g = 21/5 = 1,148...
De beginwaarde is bij T = 0  en is dus 0,5/2 = 0,25, zodat de formule wordt:  Z = 0,25 • 1,148...T
T = 17 geeft dan   Z = 0,25 • 1,148..17 ≈ 2,6 uur
   
5. Bij de top is de afgeleide nul.
Productregel:  f ' = 1 • (x2 - 16) + (x + 1) • 2x = 0
x2 - 16 + 2x2 + 2x = 0
3x2 + 2x - 16 = 0
de ABC formule geeft  x = (-2 ± √(4 + 192))/(2 • 3) =  (-2 ± 14)/6
Dat geeft  x = 2  of x = -22/3.
De gezochte oplossing is x = 2 en dan is y = (2 + 1)(22 - 16) = -36
   
6. punt P:  x = 0  ⇒  y = (0 + 1)(02 - 16) = -16.
punt Q:  y = 0  ⇒ (x + 1)(x2 - 16) = 0 
⇒  x + 1 = 0  ∨  x2 - 16 = 0
⇒  x = -1  ∨  x = 4  ∨  x = -4.
De gezochte oplossing is x = 4
k gaat door  (0, -16) en (4,0) en heeft dus helling  (0 - -16)/(4 - 0) = 4
Het begingetal is -16, dus de vergelijking wordt y = 4x - 16.  
   
7.
   
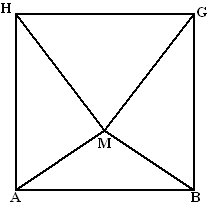
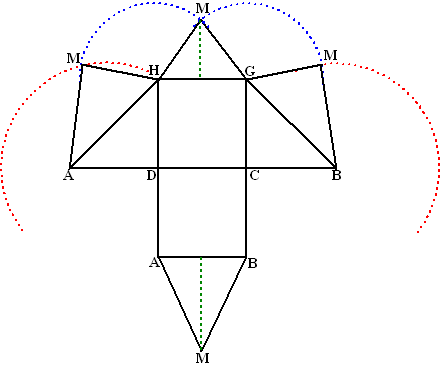
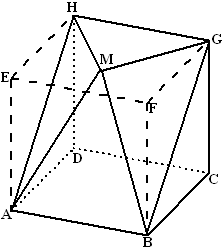
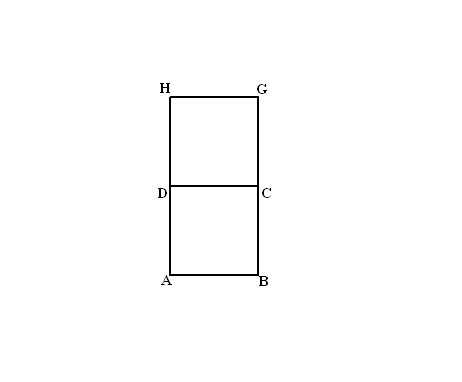
8. Teken DA = 3 cm en driehoek DAH.
Teken CB = 3 cm en driehoek CBG.

De groene lijn van M naar het midden van HG heeft lengte 4, dus op schaal is dat 2cm

De groene lijn van M naar het midden van AB heeft lengte √(22 + 62) = √40
(dat kun je zien als je in de ruimtelijke figuur van M naar het midden van EF en dan recht omlaag naar het midden van AB een driehoek tekent en Pythagoras gebruikt.
Op schaal is dat dan 0,5√40 = 3,2

Teken de rode cirkels met middelpunten B en A en straal BM

 

  Teken de blauwe cirkels met middelpunten G en H en straal GM.
De snijpunten van de cirkels geven de punten M en dus de vlakken GMB en HMA.
   
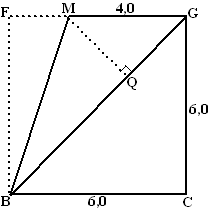
9. prisma:
Het grondvlak is driehoek BCG met oppervlakte 0,5 • 6 • 6 = 18
De hoogte is AB = 6, dus de inhoud is  18 • 6 = 108

piramide:
Driehoek MQG heeft twee hoeken van 45º. en is dus gelijkbenig.
Als MQ = x dan geldt in driehoek MQG:  x2 + x2 = 42  ofwel  x = √8 en dat is de hoogte van de piramide
Het grondvlak van de piramide is ABGH
BG2 = 62 + 62  dus BG = √72
De inhoud van de piramide is dan 1/3 • G • h = 1/3 • (√72 • 6) • √8 = 48

De totale inhoud van het lichaam is dan 108 + 48 = 156 cm3
   
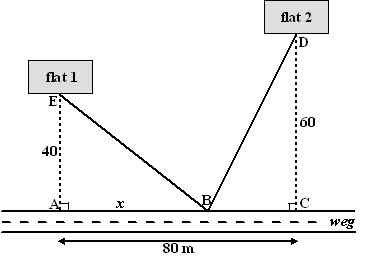
10. Gelijke lengtes betekent √(x2 + 1600) = √(x2 - 160x + 10000)
kwadrateren:  x2 + 1600 = x2 - 160x + 10000
160x = 8400 ⇒  x = 52,5 
   
11. √x = x1/2  dus de afgeleide ervan is 1/2x-1/2 = 1/2 • 1/√x = 1/(2√x)
Daar komt dan nog de kettingregel bij, en dat geeft dan als afgeleide:
 
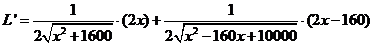  Dat moet gelijk zijn aan nul.
Voer de formule voor L' in in de GR bij Y1 = ...
Gebruik dan calc - zero en dat geeft  x = 32
Die moet je weer invullen in de oorspronkelijke formule voor L, en dat geeft  L ≈ 128 m.
Dat is dus 4 meter minder.
   
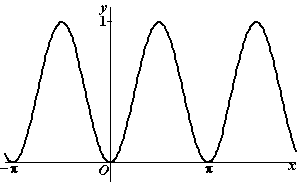
12. De evenwichtsstand is het gemiddelde van de y=coördinaten van top en dal:   (1 + 0)/2 = 1/2, dus a = 1/2
De amplitude is de verticale afstand van de top tot de evenwichtsstand, en dat is  b = 1/2
De periode is de horizontale afstand tussen twee toppen en die is p, dus  c = 2p/p = 2
Het beginpunt is waar de grafiek door de evenwichtsstand omhoog gaat en dat is bij 1/4p, dus d = 1/4p.
   
13. Met de kettingregel:  f ' = 2 • sinx • cosx
f '(1/4p) = 2 • sin(1/4p) • cos(1/4p) = 2 • 1/2√2 • 1/2√2 = 1
Dus de gevraagde helling is 1.
   
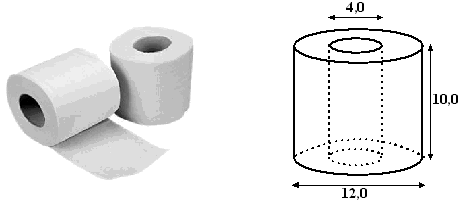
14. Buitenste cilinder:  straal is 6, dus inhoud is G • h  = p • 62 • 10 = 360p.
Binnenste cilinder:  straal is 2, dus inhoud is G • h = p • 22 • 10 = 40p.
Volume van het papier is dan 360p - 40p = 320p.  
   
15. Het volume van het papier is dan 320p/2 = 160p.
Het volume van de binnenste cilinder is 40p.
Dus het volume van de buitenste cilinder is  160p + 40p = 200p.
p • r2 • 10 = 200p ⇒  r2 = 20  ⇒ r = √20.
   
16. 12 = 2√(0,16v + 4)
⇒ 6 = √(0,16v + 4)
⇒ 36 = 0,16v + 4
⇒ 32 = 0,16v
⇒ v = 32/0,16 = 200 velletjes.
Het aantal meters papier is dan  200 • 0,136 = 27,2 meter. 
   
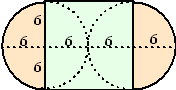
17. bovenkant en onderkant:

Hiernaast zie je dat die bestaan uit twee halve cirkels met straal 6, en een vierkant met zijden 12.

  Oppervlakte is dan 12 • 12 + p • 62 = 144 + 36p.
Dat moet twee keer

verticale gekromde vlak.
de omtrek van de bovenkant is 12 + 12 + 2p • 6 = 24 + 12p.
Als je het gekromde vlak uitvouwt krijg je dus een rechthoek met zijden 10 en 12 + 12p

totale oppervlakte is dan  2 • (144 +  36p) + 10 • (12 +  12p) ≈ 1748 cm2
   
18. log24 = log(4 • 6) = log4 + log6 = 0,6021  + 0,7782 = 1,3803
   
19. 7x = 25  ⇒  x = 7log25 = log25/log7 = log(5 • 5)/log7 = (log5 + log5)/log7 = (0,6990 + 0,6990)/0,8451 ≈ 1,654