HAVO WB, 1999 - I

 

OPGAVE 1. Een functie.
       
In de volgende figuur is de grafiek van f getekend.
       

       
6p. 1. Toon aan dat de raaklijn in de oorsprong aan de grafiek van f de vergelijking y = 2x heeft.
       
Op de grafiek van f liggen punten waarin de raaklijn aan deze grafiek evenwijdig is met de lijn y = 2x.
       
6p. 2. Bereken de x-coördinaten van deze punten.
       
6p. 3. Stel een vergelijking op van elk van de asymptoten van de grafiek van f. Licht je antwoord toe.
       
7p. 4. Los de volgende ongelijkheid op:  f(x) ≤ 1.
       
OPGAVE 2.  Bederf in de koelkast.
         
Nog steeds stellen veel Nederlandse huishoudens hun koelkast in op een te hoge temperatuur. Hierdoor kunnen producten eerder bederven dan de houdbaarheidsdatum aangeeft.
Omdat de consument steeds vaker verse producten wenst, wordt er veel onderzoek gedaan naar de houdbaarheid van producten die kunnen bederven. Een van die onderzoeken betreft het aantal pseudomonas-bacteriën per kilogram verse kip.

In de volgende figuur en de volgende vraag bekijken we de resultaten van een proef waarbij een kip werd bewaard in een koelkast die op 0 ºC is ingesteld. Er werd bijgehouden hoe het aantal bacteriën B per kilogram kip zich ontwikkelde. Om alle gegevens in één grafiek overzichtelijk te presenteren is de logaritme van B uitgezet tegen het aantal dagen d vanaf het begin van de koeling.
         

         
Volgens de Warenwet mogen er ten hoogste 50 miljoen bacteriën aanwezig zijn per kilogram kip. Zijn er meer bacteriën aanwezig dan wordt het kippenvlees afgekeurd en mag het niet meer gegeten worden.
         
5p. 5. Onderzoek met behulp van de grafiek of de kip na 10 dagen koelen op 0º C nog gegeten mag worden.
         
Eén kilogram kippenvlees dat 1000 pseudomonas-bacteriën bevat, wordt in een koelkast bewaard. De volgende formule geldt: log B = 1/3 • 1,32t • d + 3.
Hierin is B het aantal bacteriën, t de temperatuur in de koelkast in ºC en d het aantal dagen dat de kip in de koelkast wordt bewaard.

De kip blijkt, bij een bepaalde vaste temperatuurinstelling, na precies twee dagen  50 miljoen bacteriën te bevatten.
         
7p. 6. Bereken op welke temperatuur de koelkast is ingesteld. Geef je antwoord in gehele graden Celsius.
         
Uit de formule is af te leiden dat bij elke waarde van t het verband tussen B en d exponentieel is.
Neem aan dat de koelkast op 4 ºC zou zijn ingesteld.
         
5p. 7. Bereken dan de groeifactor per dag voor het aantal bacteriën B. Geef je antwoord in twee decimalen nauwkeurig.
         
OPGAVE 3. Piramide-ingang.
         
Voor de entree van een auto-showroom is als basisvorm een regelmatige piramide T.ABCD genomen. Van deze piramide is een zijkant vervangen door een overkapping T.BCFE. In onderstaande figuur staat de volledige piramide met uitbouw getekend in parallelprojectie. Deze tekening kan gebruikt worden bij de beantwoording van de volgende vragen.
         

         
Vierhoek BCEF is een gelijkbenig trapezium (BE = CF). De deurwand BCGH is verticaal. Het dak boven de deurwand steekt ver over.

Ook is gegeven:
Grondvlak ABCD is een vierkant met zijden van 6 meter.
De hoogte van de top T boven de grond is 5 meter.
         
4p. 8. Bereken in gehele graden nauwkeurig de hoek tussen de vlakken TAD en ABCD.
         
Verder is gegeven:
De hoogte van EF boven de grond is 3 meter.
De lengte van EF is 2 meter.
De afstand van EF tot vlak BCGH is 2 meter.
         
7p. 9. Bereken de afstand van T tot EF. Geef je antwoord in meters, afgerond op twee decimalen.
         
7p. 10. Teken het rechter-zijaanzicht, waarbij de kijkrichting evenwijdig is aan de lijn BA. Geef in dit zijaanzicht vierhoek BCGH aan. Licht je werkwijze toe.
         
7p. 11. Bereken de oppervlakte van de deurwand BCGH. Geef je antwoord in m2,  in twee decimalen.
         
OPGAVE 4. Kortste aansluiting.
         
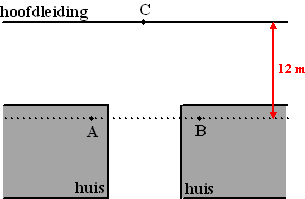
In een nieuwbouwwijk moeten twee huizen worden aangesloten op het waterleidingnet. In de volgende figuur is de situatie geschetst.
         

         
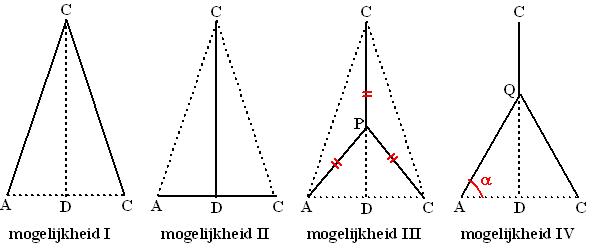
In het punt C wordt een aftakking gemaakt van de hoofdleiding naar de punten A en B in de huizen.
De punten A, B en C liggen zo dat driehoek ABC gelijkbenig is met AC = BC en AB = 8 meter. De hoofdleiding loopt evenwijdig aan AB op een afstand van 12 meter van de lijn door A en B.

De verbinding tussen C en de beide huizen kan op verschillende manieren worden gelegd. In de figuur hieronder zijn vier mogelijkheden aangegeven. De vragen 12, 13, 14 en 15 gaan over deze mogelijkheden.
         

         
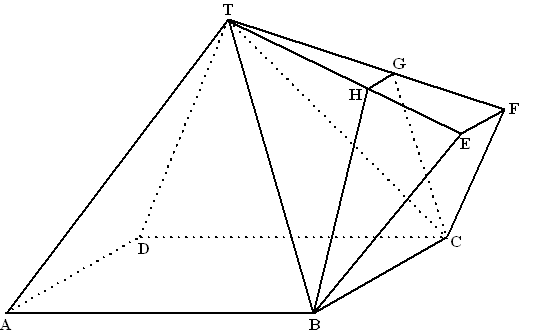
Eerst bekijken we de mogelijkheden I en II:
I:  Vanaf C twee rechtstreekse leidingen CA en CB.
II: Vanaf C een leiding naar het midden D van AB, die vervolgens vertakt naar A en B.
         
6p. 12. Onderzoek bij welke van de mogelijkheden I en II de totale lengte van de verbinding het kortst is.
         
Vervolgens bekijken we mogelijkheid III:
III: Vanaf C een leiding naar een punt P op de symmetrieas CD van driehoek ABC en vervolgens vanuit P vertakkingen naar A en B zodat  CP = PA = PB.
         
7p. 13. Bereken de totale lengte van de verbinding bij mogelijkheid III.
         
Tenslotte bekijken we nog mogelijkheid IV:
IV: Vanaf C een leiding naar een punt Q op CD en vanuit Q vertakkingen naar A en B. De totale lengte van de verbindingsleidingen tussen C en de huizen hangt af van hoek α tussen AQ en AB.
         
De totale lengte L(a) van de verbinding wordt dan voor elke toegestane waarde van a gegeven door de formule:
 
         
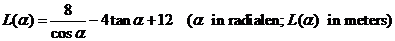5p. 14. Toon de juistheid van deze formule aan.
         
Er is een punt Q op CD zo dat de totale lengte L(α) minimaal is.
         
5p. 15. Bereken de bijbehorende waarde van α.
         

 

UITWERKING
   
1.  
   
2.  
   
3.  
   
4.  
   
5.  
   
6.  
   
7.  
   
8.  
   
9.  
   
10.  
   
11.  
   
12.  
   
13.  
   
14.  
   
15.  
   
16.  
   
17.  
   
18.  
   
19.  
   
20.  
   
21.  
   
22.  
   
23.