OPGAVE 1.
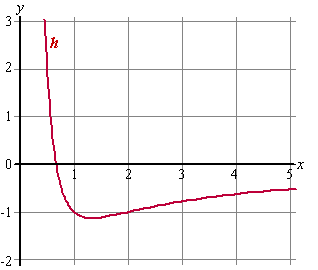
Hieronder is een deel van de grafiek van die functie getekend.
	1.	Bereken de x-coördinaat van het snijpunt van de grafiek van h met de x-as.
	2.	Los op:  h(x) <  -5/8
Gegeven is de functie: f(x) =  -2/x - ln(x3)  voor x > 0.
	3.	Laat met behulp van de regels voor het differentiëren zien dat h de afgeleide functie is van f.
	4.	Bereken de uiterste waarde van f(x) in twee decimalen nauwkeurig en onderzoek of dit een maximum dan wel een minimum is.
Aan de grafiek van h is te zien dat de grafiek van f een buigpunt heeft tussen x = 0 en x = 5.
	5.	Bereken de x-coördinaat van het buigpunt van de grafiek van f
De functie h is ook de afgeleide functie van een functie g waarvan bekend is dat de grafiek door het punt (1,0) gaat.
	6.	Door welke formule wordt g(x) uitgedrukt in x?

OPGAVE 2.
Het gebouw op deze foto heeft een balkenconstructie waaraan via staalkabels het dak is opgehangen. In de figuur hieronder is het gebouw getekend in een scheve projectie, waarbij het vierkante dak in ware vorm is afgebeeld. De afmetingen in de drie hoofdrichtingen x, y en z zijn alle drie op dezelfde schaal weergegeven: 1 cm in de tekening komt overeen met 2 meter. Het dak bestaat uit 25 vierkanten van 3 bij 3 meter.
	7.	Hoe lang is kabel c? Geef je antwoord in dm nauwkeurig.
Als je op grote afstand om het gebouw heen loopt, zie je het gebouw nagenoeg in parallelprojectie. Bij een aantal kijkrichtingen lijken verschillende kabels samen te vallen.
	8.	Is er een kijkrichting mogelijk waarbij kabel a en kabel b lijken samen te vallen? Licht je antwoord toe.
	9.	Is er een kijkrichting mogelijk waarbij kabel a en kabel c lijken samen te vallen? Licht je antwoord toe.
	10.	Teken, uitgaande van bovenstaande figuur, een aanzicht in de x-richting van het gebouw met balken en kabels.

OPGAVE 3.
Een luchtkussen is in een machine aangebracht om trillingen van een onderdeel op te vangen. Het volume van het luchtkussen verandert daarbij voortdurend. Daarmee samenhangend verandert ook de luchtdruk in het kussen. Het volume (V) en de luchtdruk (P) zijn beiden functies van de tijd t. Het verband tussen luchtdruk en volume wordt gegeven door de formule:
Gemakshalve worden hier voor de grootheden volume, druk en tijd niet nader gespecificeerde eenheden gebruikt. In de volgende figuur is de grafiek van V als functie van t getekend.
Op t = 5 geldt:  V = 0,5  en  dV/dt = 0,25
	11.	Bereken dP/dt voor t = 5
	12.	Teken in de figuur hierboven de grafiek van P als functie van t

OPGAVE 4.
Voor het kweken van plantjes gebruikt een tuinder een cellenstructuur zoals in de figuur hier onder links is afgebeeld. Iedere afzonderlijke cel heeft zes zijden van 3 cm. Door de hele structuur uit te rekken zolas aangegeven in de figuur rechts, verandert de vorm van iedere cel. Daarbij blijven EF en CB evenwijdig. Die verandering kan worden beschreven met behulp van de variabele hoek DAB. Stel de grootte van hoek DAB is x radialen.
	13.	Bereken x in radialen (in 2 decimalen nauwkeurig) in het geval dat BF = 4
Het verband tussen de oppervlakte van de cel (S) en de hoekgrootte (x) wordt gegeven door: S = 18sinx + 18sinxcosx
	14.	Bewijs de juistheid van deze formule.
	15.	Druk dS/dx uit in cosx
	16.	Bereken voor welke waarde van x de oppervlakte van de cel maximaal is.

OPGAVE 5.
In een betonconstructie kruisen twee horizontale balken elkaar loodrecht (zie de figuur linksonder). De afstand tussen de balken is 6 m. De balken zijn verbonden door een zuil met rechthoekig boven- en ondervlak (zie figuur rechtsonder). De middelpunten van de rechthoeken liggen recht boven elkaar. Beide rechthoeken zijn 1m bij 4m. Helemaal rechtsonder zie je een bovenaanzicht van de zuil.
De vier opstaande zijvlakken van de zuil maken elk een even grote hoek met het horizontale vlak.
	17.	Bereken de grootte van die hoek in graden nauwkeurig.
Er wordt een kartonnen model van de zuil gemaakt op schaal 1 : 100.
	18.	Teken een bouwplaat voor dit model. De bouwplaat mag niet uit losse stukken bestaan en de plakrandjes hoeven niet te worden getekend.
Rondom de zuil wordt, op halve hoogte en horizontaal, een lint strak gespannen.
	19.	Bereken hoe lang dat lint is.
	20.	Is het mogelijk om het lint langs de zuil omhoog (of omlaag) te schuiven, zó, dat het lint horizontaal en strak gespannen blijft? Licht je antwoord toe.

UITWERKING
1.	x = 2/3
2.	4/5 < x < 4
3.
4.	f(2/3) = -1,78
5.	x = 4/3
6.
7.	94 dm
8.	ja
9.	nee
10.
11.	dP/dt = -1
12.
13.	0,73 rad
14.
15.
16.	x = 1/3p
17.	76º
18.
19.	10 m
20.	ja, dat kan