OPGAVE 1.
Gegeven is de functie f(x) = 10xe-x  voor  0 ≤ x ≤  5. Hieronder is de grafiek van die functie getekend.
De grafiek van f begint in O
	1.	Bereken de hoek die de grafiek in O met de x-as maakt (in graden nauwkeurig).
	2.	Bereken de grootste functiewaarde van f (in twee decimalen nauwkeurig).
Op de grafiek van f ligt een punt A zodanig, dat de hellingscoëfficiënt van de lijn OA gelijk is aan 2.
	3.	Bereken de coördinaten van A (in twee decimalen nauwkeurig).

OPGAVE 2.
In een Oxyz-assenstelsel ligt de kubus OPQR.KLMN met ribbe 6. Hierboven is die kubus in scheve projectie getekend. Het vlak U gaat door K, R, het midden A van LP en het midden B van PQ.
	4.	Bereken de oppervlakte van vierhoek ABRK.
Het vlak U wordt in de richting van de positieve z-as 1 eenheid omhooggeschoven. Zo ontstaat vlak V.
	5.	Teken de doorsnijdingsfiguur van V met de kubus.
Het diagonaalvlak OPMN is een rechthoek. Het vlak U snijdt dit diagonaalvlak volgens een lijn l.
	6.	Teken de lijn l in de rechthoek hiernaast.
Het vlak U draait om de lijn KR. Het snijpunt A van U met LP verandert daardoor van plaats. Neem aan dat het punt A juist alle posities op de ribbe LP bereikt.
	7.	Arceer in de rechthoek hiernaast het gebied dat bestreken wordt door de snijlijn l van U met het diagonaalvlak OPMN.

OPGAVE 3.
Van een diersoort in een bepaald gebied wordt het aantal N afhankelijk van de tijd t bekeken. Er blijkt dat log N lineair afhangt van log t volgens de formule:  logN = 3 + 0,75 • logt  voor t ≥ 1 N kan geschreven worden in de vorm N = a • tb  .
	8.	Bereken a en b.
	9.	Toon aan dat er sprake is van afnemende groei.

OPGAVE 4.
In de figuur hierboven zie je de grafieken I en II. I is de grafiek van y = x3 . Grafiek II ligt rechts van I, zodanig dat alle horizontale verbindingslijnstukken van I en II lengte 2 hebben. De verticale verbindingslijnstukken van I en II variëren in lengte.
	10.	Bewijs dat er een kortste verticaal verbindingslijnstuk is en bereken de lengte daarvan.

OPGAVE 5.
Hier linksboven zie je een schets van een gebouw dat uit twee lagen bestaat. De tweede laag, het bovendeel bestaat uit schuine zijvlakken en een dak. Vier van die zijvlakken zijn rechthoekig, de andere vier zijn driehoekig. In de figuur rechts zie je een bovenaanzicht van het bovendeel. De hoogte van het bovendeel is 2,80 meter. In de figuur hieronder is in parallelprojectie het bovenvlak van het onderste deel van het gebouw getekend.
	11.	Teken in deze figuur het bovendeel. Geef niet-zichtbare lijnen met een stippellijn aan.
Het bovendeel heeft 8 schuine zijvlakken. Elk van deze zijvlakken heeft een hellingshoek.
	12.	Bereken de verschillende hellingshoeken (in graden nauwkeurig)
	13.	Bereken de inhoud van het bovendeel.
Stel je voor dat de vier grote schuine zijvlakken naar boven toe worden doorgetrokken. Er ontstaat dan bovenop de tweede laag een dakvorm met een nok.
	14.	Teken de nok in het bovenaanzicht hiernaast.

OPGAVE 6.
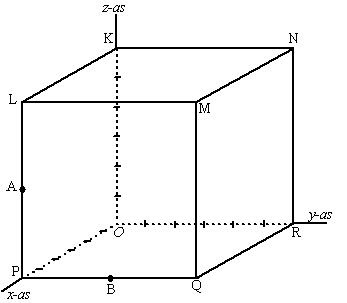
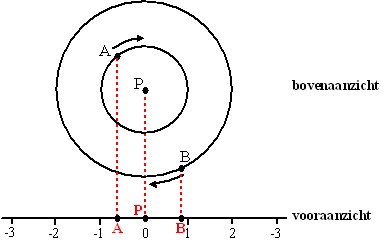
Voor een animatiefilm wordt de beweging van twee manen A en B rond een planeet P gesimuleerd. De banen worden als cirkels in één vlak gekozen. In de onderstaande figuur zie je het bovenaanzicht van een situatie op een bepaald moment. A en B bewegen in de richting van de pijl.
In het vooraanzicht bewegen A en B zich over een rechte lijn volgens de formules: xA = sin2πt  en  xB = 2sinπt  (t is de tijd in seconden). Hierin geven xA en xB de plaatsen van A respectievelijk B ten opzichte van P aan in het vooraanzicht.
	15.	Teken in het vooraanzicht en het bovenaanzicht de posities van A en B op het tijdstip t = 0,75.
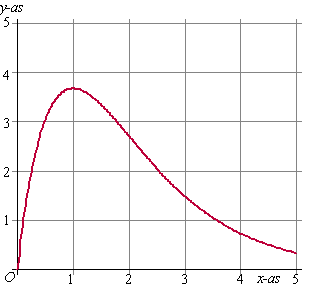
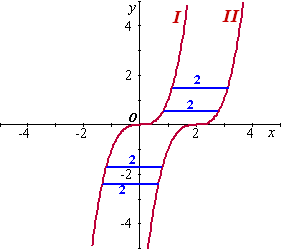
	16.	Teken in één figuur de grafieken van xA en xB als functie van t voor  0 ≤ t ≤ 2.
In het bovenaanzicht zie je voortdurend de werkelijke verhouding van de afstanden AP en BP, namelijk 2 : 1, in het vooraanzicht meestal niet.
	17.	Op welke tijdstippen in het tijdsinterval [0, 2] zie je in het vooraanzicht B twee keer zo ver van P als A? Beschouw alleen de situaties waarbij A en B aan dezelfde kant van P liggen.
Er is een kunstmaan C gelanceerd. Deze kunstmaan is bedoeld om A van dichtbij te bestuderen. C bevindt zich in dezelfde baan als A en cirkelt met dezelfde snelheid als A en in dezelfde richting rond P. C ligt 0,1 seconde voor op A. C wordt toegevoegd aan de animatiefilm.
	18.	Geef een formule voor de plaats xC in het vooraanzicht als functie van t.

UITWERKING
1.	84º
2.	f(1) = 3,68
3.	A(1,61; 3,22)
4.	40,5
5.
6.
7.
8.	a = 1000,  b = 0,75
9.
10.	v(1) = 2
11.
12.	69º
13.	152,6 m3
14.
15.	xA = -1 en  xB = √2
16.
17.	t = 1/3  en  t = 12/3
18.	xC = sin2p(t + 0,1)