HAVO WB12, 2006 - II

 

Toename lichaamsgewicht zwangere vrouw.
Een vrouwenarts heeft van een zwangere vrouw gedurende de zwangerschap allerlei gegevens verzameld. In de volgende tabel staan enkele resultaten. Daaruit is onder andere af te lezen dat deze vrouw als ze 25 weken zwanger is, sinds het begin van de zwangerschap 3030 gram zwaarder is geworden.
Aantal weken zwanger 15 25 35 40
Toename lichaamsgewicht in gram
(afgerond op tientallen)		 1520 3030 5990 8400
Het verband tussen het aantal weken zwangerschap en de gewichtstoename van deze vrouw is vanaf de vijftiende week bij benadering exponentieel.
4p

1.

 Bereken de groeifactor per week van dit exponentiële verband.
Rond je antwoord af op twee decimalen.

 
De gewichtstoename van een zwangere vrouw wordt voor een deel veroorzaakt door het gewicht van de ongeboren baby. Onderzoek toont aan dat vanaf week 20 dit gewicht elke week ongeveer evenveel toeneemt.
In de volgende tabel zijn gewichten weergegeven van het ongeboren kind van de vrouw van wie de gewichtstoename in de tabel hierboven staat.
Aantal weken zwanger 20 25 35 40
Gewicht van het ongeboren
kind in gram		 523 1390 3120 3990
De formule F = a • t  + b  geeft bij benadering het verband  weer tussen het gewicht van het ongeboren kind en de duur van de zwangerschap. Hierin is t de tijd in weken dat de vrouw zwanger is, en F het gewicht van het ongeboren kind in gram.
4p

2.

 Bereken a en b met behulp van de gegevens uit de tabel.

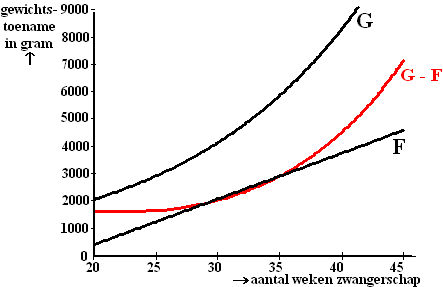
Tijdens de zwangerschap van een andere vrouw zijn ook de gewichtstoename van de moeder en het gewicht van het ongeboren kind door de vrouwenarts bijgehouden. De gegevens zijn in formules verwerkt. De bijbehorende grafieken zijn hieronder afgebeeld.

De formules die bij deze zwangerschap horen zijn:  G = 1450 • 20,1t - 1,5  en  F = 165t - 2875.
Hierin is t de duur van de zwangerschap in weken , G de gewichtstoename van de vrouw in gram en F het gewicht van het ongeboren kind in gram.
In de figuur is met rode kleur de grafiek getekend van het verschil tussen G en F.

Aan het eind van de zwangerschap wordt er veel vocht opgeslagen. Ook neemt het gewicht van de vrouw toe door weefselvorming rond het ongeboren kind. Aan het eind van de zwangerschap kunnen G en F wel 4000 tot 8000 gram verschillen.
5p

3.

 Bereken met behulp van de gegeven formules op welke dag na het begin van de zwangerschap bij deze vrouw dit verschil voor het eerst meer dan 4000 gram is.

De grafiek van F en de verschilgrafiek snijden elkaar voor twee waarden van t. Op deze twee tijdstippen geldt dat G twee keer zo groot is als F.
4p

4.

 Beredeneer dit zonder deze snijpunten met behulp van de formules uit te rekenen.

5p

5.

 Beredeneer met behulp van differentiëren voor welke waarde van t de gewichtstoename G van de moeder en het gewicht F van het ongeboren kind even snel toenemen.

 

Functies.
Gegeven is de functie  f(x) = x4 - 16.
De grafiek van f snijdt de x-as in de punten (-2, 0) en (2, 0).
Door de grafiek van f omlaag te schuiven veranderen de snijpunten met de x-as in de punten (-3, 0) en (3, 0).
In de figuur hiernaast zijn de grafiek van f en de verschoven grafiek getekend.

3p

6.

 Bereken over welke afstand de grafiek van f  in deze situatie omlaag verschoven is.

De raaklijn aan de grafiek van f  in het punt (2, 0) is de lijn k.
De lijn m gaat door het punt (-2, 0) en is evenwijdig aan de lijn k (zie de middelste figuur hiernaast)
4p

7.

 Stel met behulp van differentiëren een vergelijking op van de lijn m.

Door f(x) met x3 te vermenigvuldigen ontstaat de productfunctie  g(x) = x3 (x4 - 16).
In de onderste figuur hiernaast is de grafiek van g getekend.
6p

8.

 Bereken exact de x-coördinaten van de toppen van de grafiek van g.

 

Prisma.
In de figuur hiernaast is het prisma ABC.DEF getekend. De ribben AD, BE en CF staan loodrecht op de vlakken ABC en DEF.
De driehoeken ABC en DEF zijn gelijkzijdig met zijden van 6 cm.
Ook de opstaande ribben van het prisma hebben een lengte van 6 cm.

Het vlak BDF verdeelt het prisma in twee piramides (zie figuur).

5p

9.

 Bereken de inhoud van de piramide B.ACFD. Geef je antwoord in cm3 nauwkeurig.

P is het midden van ribbe EF.
Lijn AP snijdt vlak BDF in punt S.
5p

10.

 Teken het punt S. Licht je werkwijze toe.

6p

11.

 Bereken de hoek die lijn BD met vlak ACFD maakt. Geef je antwoord in gehele graden.

In de figuur linksonder is een draadmodel afgebeeld van het beschreven prisma ABC.DEF. De stukken draad kunnen scharnieren in de hoekpunten.
Door druk uit te oefenen op punt D in de richting van punt P verandert het rechte prisma in een scheef prisma. De lengtes van de ribben blijven daarbij het zelfde. Zie de figuur rechtsonder.
De drie opstaande ribben AD, BE en CF staan nu niet meer loodrecht op de vlakken ABC en DEF.

Men drukt tot de hoogte van het scheve prisma de helft is van de hoogte van het rechte prisma. Hieronder staat een gedeelte van het bovenaanzicht van het prisma in zijn eindpositie.

6p

12.

 Teken het volledige bovenaanzicht van het scheve prisma op ware grootte. Licht je antwoord toe.

 

Trillende stemvorken.
Bij een stemvork die in trilling gebracht wordt, maken de uiteinden zeer snelle heen en weergaande bewegingen rond de evenwichtsstand. De afstand van een uiteinde tot deze evenwichtsstand heet de uitwijking.De grafiek van de uitwijking y, afhankelijk van de tijd t, is een sinusoïde. De trilling van de stemvork brengt de lucht in trilling. Dit horen wij als geluid.

Hierboven staan twee stemvorken A en B afgebeeld. Met behulp van een oscilloscoop krijgt men de grafiek van het trillingspatroon. In de figuur rechts staat de grafiek voor stemvork A.
Bij deze grafiek hoort de formule:

Stemvork A:  y = 0,28 • sin(0,88πt)

Hierin is t de tijd in milliseconden (1 milliseconde is 0,001 seconde) en y de uitwijking in millimeters.
De trilling van stemvork A begint op t = 0.
4p

13.

 Bereken het aantal trillingen per seconde voor stemvork A.

Als de frequentie groter wordt wordt de toon hoger.
Als de amplitude (maximale uitwijking) groter wordt, wordt het geluid harder.
Voor stemvork B geldt de formule:

Stemvork B:   y = 0,14 • sin(0,88π(t - 0,5))

De beide stemvorken klinken dus even hoog, maar stemvork B klinkt zachter dan stemvork A.
Een derde stemvork C:
• klinkt hoger dan de stemvorken A en B.
• klinkt harder dan stemvork B, maar zachter dan stemvork A.
3p

14.

 Stel een formule op voor de trilling van stemvork C.

Na het in trilling brengen wordt het geluid van een stemvork langzaam zachter. De frequentie van de trilling verandert hierbij niet, maar de amplitude neemt geleidelijk af. Op het scherm van de oscilloscoop is dit te zien.

In figuur A is het scherm van de oscilloscoop te zien vlak nadat stemvork A op tijdstip t = 0 in trilling is gebracht.
In figuur B zie je het scherm van de oscilloscoop na ongeveer 5000 milliseconden.
Duidelijk is te zien dat de amplitude nu kleiner is.
Weer enige tijd later ziet het scherm van de oscilloscoop er uit als in figuur C. De amplitude is nu 1/10 van de oorspronkelijke amplitude.
Bij de grafiek hoort de volgende formule:

y = e -0,0001t • 0,28 • sin(0,88πt)    met t in milliseconden en y in millimeters.
5p

15.

 Onderzoek hoeveel seconden na het begin van de trilling het scherm van figuur C te zien is. Rond je antwoord af op gehele seconden.

Warmtebalans.
De temperatuur van een gekoeld pakje of blikje frisdrank stijgt op een zonnig strand snel. Dit heeft verschillende oorzaken. We beperken ons in deze opgave tot de oppervlakte en het volume van de verpakking.
Als een verpakking bij dezelfde inhoud een grotere oppervlakte heeft, zal de frisdrank erin sneller opwarmen. Hiervoor is de warmte-uitwisselingsfactor F van belang.
Er geldt:  F = A/V  waarbij A de totale oppervlakte van de verpakking is in cm2 en V het volume in cm3 .

We bekijken een balkvormige en een cilindervormige verpakking van frisdrank. Zie de figuren hieronder. In deze figuren zijn tevens de afmetingen in cm aangegeven.
Voor de oppervlakte A van de cilinder geldt  A = 2πr2 + 2πrh,  waarbij h de hoogte is en r de straal van het grondvlak.

In beide verpakkingen gaat vrijwel dezelfde hoeveelheid frisdrank.
De warmte-uitwisselingsfactor F is verschillend.
6p

16.

 Onderzoek welke verpakking de kleinste F-waarde heeft.
Voor een groot koffiezetapparaat moet een cilindervormige tank worden ontworpen met een inhoud van 8 liter (1 liter = 1000 cm3). Noem de straal van het grondvlak van deze tank r en de hoogte van deze tank h (r en h in cm).

De hoogte h van de tank kun je uitdrukken in de straal r.  Er geldt:

Een eis die men aan het ontwerp van het koffiezetapparaat stelt, is dat de hoogte h tussen de 20 cm en 40 cm ligt.

5p

17.

 Bereken welke waarden voor de straal r dan zijn toegestaan. Rond de getallen in je antwoord af op één decimaal.

In plaats van grenzen aan de hoogte te stellen zou men ook de volgende eis kunnen stellen:
"De afmetingen van de tank moeten zodanig zijn dat de koffie er zo lang mogelijk warm in blijft. Dat wordt bereikt als de warmte-uitwisselingsfactor F van de tank zo klein mogelijk is".
Voor de warmte-uitwisselingsfactor van een cilindervormige tank met een inhoud van 8 liter heeft men de volgende formule gevonden:
5p

18.

 Bereken met behulp van differentiëren de straal van een tank die aan deze eis voldoet.
Rond de getallen in je antwoord af op één decimaal. 

OPLOSSING
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
1. In 25 weken is de factor  8400/1520 = 5,526
Per week is dat 5,5261/25 ≈ 1,07
2. In 20 weken groeit het kind 3990 - 523 = 3467 gram, dat is per week 173,35 gram, dus a = 173,35
De vergelijking moet dus zijn F = 173,35  t + b
Vul bijv.  (20, 523) in:  523 = 173,35 • 20 + b  ⇒  b  = -2944
(Met andere getallen uit de tabel kun je iets afwijkende antwoorden krijgen)
3. G - F = 1450 • 20,1t - 1,5 - 165t + 2875
Plot deze grafiek bij Y1.
Neem bijv  window  Xmin =0,  Xmax = 50,  Ymin = 0,  Ymax = 8000
intersect geeft  X = 38,742 weken en dat is ongeveer dag  38,742 • 7 = 271 
4. In het snijpunt geldt: F = G - F.
Breng de F rechts naar de andere kant. Dat geeft  2F = G en daarmee is 't alweer bewezen!
5. De toenames zijn gelijk als de afgeleides gelijk zijn.
F' = 165
G'= 1450 • 20,1t - 1,5 • ln2 • 0,1   (de factor 0,1 komt van de kettingregel)
F'= G' ⇒  165 = 1450 • 20,1t - 1,5 • ln2 • 0,1  
 ⇒  165 ≈ 100,51 • 20,1t - 1,5 
 ⇒  1,64 ≈ 20,1t - 1,5 
⇒  0,1t - 1,5 = 2log1,64 = log 1,64/log 2 ≈ 0,715
⇒  0,1t = 2,215  
⇒  t ≈ 22,15 weken en dat is ongeveer 155 dagen.

(maar het kan natuurlijk ook allemaal met de GR en intersect...(zucht))
6. x4 - 81 snijdt de x-as in (-3,0) en (3,0)  (want 34 = 81)
Dat is x4 - 16 - 65 dus de grafiek moet 65 omlaag worden geschoven.

of;
bij x = 3  is  f(x) = 34 - 16 = 65, en dat moet nul worden, dus 65 omlaag.
7. f '(x) = 4x3 , dus  f '(2) = 32.
De raaklijn m heeft dus ook hellinggetal 32, en vergelijking  y = 32x + b 
De lijn moet door (-2, 0) gaan, dus  0 = 32• -2 + b  ofwel  b = 64
De vergelijking is dan y = 32x + 64
8. In de toppen geldt g'(x) = 0
g'(x) = 3x2 (x4 - 16) + x3 • 4x3   (met de productregel) = 0
⇒  3x6 - 48x2 + 4x6 = 0
⇒  7x6 - 48x2 = 0
⇒  x2 (7x4 - 48) = 0  ⇒  x2 = 0  of  7x4 = 48
De eerste geeft x = 0, maar dat is het buigpunt.
De tweede vergelijking geeft  x4 = 48/7 ⇒  x = (48/7)1/4  of  x = -(48/7)1/4 
9. Het grondvlak is ACFD en heeft oppervlakte 6 • 6 = 36
De hoogte h is de lengte van het lijnstuk van B naar het midden van AC (dat staat loodrecht op ACFD)
Pythagoras geeft  h2 + 32 = 62  ⇒  h = √27
De inhoud is dan 1/3 • 36 • √27  ≈ 62 cm3 
10. Hulpvlak PQAD  (PQ evenwijdig aan EB)

Snijlijn van de vlakken is RD  (R snijpunt van PQ en BF)

Gevraagde punt is S: snijpunt van RD en AP.

11. De projectie van B op ACDF is het midden M van AC.
Het gaat om ∠BDM.
In driehoek BDM is hoek M 90º.
BD = √(62 + 62 ) = √72  en  BM = √27  (zie vraag 9)
sin ∠BDM = √27/√72 = 0,6124  ⇒  ∠BDM ≈ 38º 
12. Noem de projectie van D op het grondvlak D'.
AD = 6,  en DD' = 3 geeft  AD' = √27
Dat is precies gelijk aan DP, dus als de hoogte 3 is, ligt punt D precies boven het midden van CD.

Dat geeft het bovenaanzicht hiernaast.
13. de periode is  (2π)/(0,88π) = 2/0,88 = 2,2727 milliseconde, en dat is 0,002727 seconden
de frequentie is dan 1/0,002727 = 367 trillingen per seconde.
14. De amplitude ligt tussen 0,14 en 0,28
De periode is kleiner dan die van A en B, dus het getal in de formule voorde t is groter dan 0,88.
Bijv.  y = 0,2 • sin(t)
15. De amplitude is 0,028, dus moet gelden  e -0,0001t = 0,1
⇒ -0,0001t = ln 0,1  = -2,30  Þ  t = -2,30/-0,0001 = 23026 milliseconden en dat is ongeveer 23 seconden.
16. Balk:
inhoud 7,5 • 4 • 10 = 300
oppervlakte  2 • 4 • 7,5 + 2 • 4 • 10 + 2 • 10 • 7,5 = 290
F = 290/300 ≈ 0,97

Cilinder:
inhoud  π • 32 • 10,6 » 299,71
oppervlakte  2π • 32 + 2π • 3 • 10,6 » 256,35
F = 256,35/299,71 ≈ 0,86

Dus de cilinder heeft de kleinste F.
17. h = 8000/(pr2 )  geeft  r2 = 8000/(ph)
h = 20 levert  r2 = 127,32  ⇒  r = 11,3
h = 40 levert r2 = 63,66  ⇒   r = 8,0
De waarden tussen 8,0 en 11,3 zijn dan toegestaan.
18. F = 2r -1 + π/4000 • r2
F '= -2r -2 + 2π/4000 • r = 0
vermenigvuldig alles met r2 :  -2 + 2π/4000 • r3 = 0
⇒  2π/4000 • r3 = 2
⇒  0,00157 • r3 = 2
⇒  r3 = 1273,24
⇒  r = (1273,24)1/3 ≈ 10,8 cm