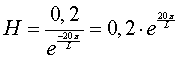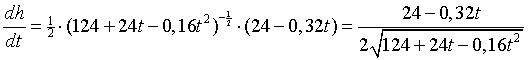HAVO WB12,  2005 - I
Modderstroom
Er zijn vulkanen die geen lava uitspuwen, maar een constante stroom modder geven. De koude modder stroomt als een rivier langzaam de helling af. Zie de bovenste foto hiernaast.
Aan de rand van deze stroom droogt de modder op. Daar stroomt de modder dus wat langzamer dan in het midden.
Dat is te zien aan het geribbelde patroon.

Om dit snelheidsverschil te meten gebruiken geologen stenen die ze op de modderstroom leggen. Bij een modderstroom van ruim 6 dm breed gebeurt dat als volgt. Een geoloog legt een rij van 7 stenen  dwars in de stroom. Elke steen krijgt een nummer van 0 t/m 6. Steen nummer 0 legt hij vlak bij de rand van de stroom. Het midden van steen nummer 1 legt hij op 1 dm afstand van het midden van steen nummer 0. De afstand tussen de middens van opeenvolgende stenen is steeds 1 dm. Steen nummer 6 ligt vlak bij de andere rand.
Het resultaat zie je op de onderste foto hiernaast.

Elk uur meet hij de afstand die de stenen door de stroom hebben afgelegd. In de onderstaande figuren zie je de ligging na één uur en na drie uur.

De afstand A (in dm) die de stenen na één uur hebben afgelegd, wordt beschreven door de formule:
A = -0,1x2 + 0,6x + 19,4
Hierbij is x de afstand in dm van het midden van een steen tot het midden van steen 0 bij het begin van het proces.
3p

1.

 Bereken de afstand die steen nummer 2 het eerste uur heeft afgelegd.
De stenen gaan met de modder mee de berg af. Elke steen heeft zijn eigen constante snelheid.
4p

2.

 Van welke stenen ligt die snelheid het dichtst bij 20 dm per uur?
licht je antwoord toe met een berekening.

 
De geoloog heeft de stenen op een rechte lijn loodrecht op de stroomrichting gelegd. Steen nummer 3 zal door de stroom sneller vooruitkomen dan de andere stenen. Het weglengte verschil W dat op die manier tussen steen nummer 3 en steen nummer 6 na één uur ontstaat is afgebeeld in de figuur hiernaast.
3p

3.

 Toon aan dat het weglengteverschil W tussen steen nummer 3 en steen nummer 6 na één uur 9 cm is.
Op een gegeven moment meet de geoloog een weglengteverschil W tussen steen nummer 3 en steen nummer 6 van 83 cm.
4p

4.

 Bereken de totale afgelegde weg van de steen met nummer 3 gerekend vanaf de plek waar de geoloog de stenen in de modderstroom gelegd heeft.
Geef je antwoord in cm nauwkeurig.

Zeegolven
De meeste golven in de oceanen worden veroorzaakt door de wind. Hierbij gaat elk waterdeeltje afwisselend omhoog en omlaag. Als het water niet stroomt, komen de waterdeeltjes bij deze golfbeweging weer op hun oorspronkelijke plaats terug. Gebleken is dat ze niet verticaal op en neer gaan, maar een cirkelbaan maken in een verticaal vlak. De diameter van zo'n cirkel is kleiner naarmate het waterdeeltje dieper onder het zeeoppervlak ligt. Zie de figuur hieronder.
De diameter van de cirkelbaan die een waterdeeltje aan het oppervlak maakt, is gelijk aan de hoogte van de golf (= verschil tussen maximale en minimale hoogte van de golf).

Het is gebleken dat het verband tussen de diameter van de cirkelbaan en de diepte van het waterdeeltje exponentieel is.
In een bepaalde situatie geldt de volgende formule:
d = 3 • 0,76x

Hierin is:
•  x de diepte van het waterdeeltje in meters
•  d de diameter van de cirkelbaan die het waterdeeltje maakt op diepte x, ook in meters.
3p

5.

 Bereken hoeveel keer zo groot de diameter op 0 meter diepte is als de diameter op 25 meter diepte.
Bij een golfhoogte van 5 meter is onderzoek gedaan naar het verband tussen de diepte van het waterdeeltje en de diameter van de bijbehorende cirkel. Een gedeelte van de resultaten is te zien in de volgende tabel:
Diepte (in m) 0 5 15
Diameter (in m) 5,000 1,060 0,048
3p

6.

 Laat door een berekening zien dat de gegevens in bovenstaande tabel ongeveer passen in een exponentieel model.

De diameter d van de cirkelbaan van een waterdeeltje is niet alleen afhankelijk van de diepte van het waterdeeltje maar ook van de golflengte en de hoogte van de golf.
Er geldt de volgende formule:

Hierin is:
• x de diepte van het waterdeeltje
• d de diameter van de cirkelbaan die het waterdeeltje maakt op diepte x
• H de hoogte van de golf aan het zee-oppervlak
• L de golflengte gemeten aan het zee-oppervlak.
Alle lengtes zijn in meters.

In de situatie van de tabel is de hoogte van de golf aan het zee-oppervlak 5 meter. Verder blijkt uit de tabel dat op een diepte van 5 meter de diameter van de cirkelbaan 1,060 meter is.

4p

7.

 Bereken met behulp van deze gegevens de golflengte aan het zee-oppervlak.
Geef je antwoord in cm nauwkeurig.

Onderzoekers die in een duikboot in de oceanen de zwaartekracht bepalen, moeten om nauwkeurige meetresultaten te krijgen geen last hebben van bewegingen in het water. Ze gaan daarom zo diep duiken dat de diameter van de cirkelbaan van een waterdeeltje op de betreffende diepte niet groter is dan 0,01 mm.

Bij de volgende vraag gaan we ervan uit dat aan het zee-oppervlak de golfhoogte 5 meter is en de golflengte 100 meter.
5p

8.

 Bereken vanaf welke diepte de diameter van de cirkelbaan van de waterdeeltjes kleiner is dan 0,01 mm. Rond je antwoord af op gehele meters.

Neem aan dat op een diepte van 10 meter de diameter d gelijk is aan 0,2. In deze situatie zijn verschillende waarden van H en L mogelijk. Er bestaat een verband tussen L en H.
Zie de figuur hiernaast.

De gegeven formule d = H • e(-2πx/L) kan voor deze situatie worden omgewerkt tot een formule waarbij H wordt uitgedrukt in L.
3p

9.

 Druk H uit in L.

Uitkijktoren
Om bij mooi strandweer de mensen in zee in de gaten te kunnen houden gebruikt de strandwacht een lichtgewicht uitkijktoren. Het frame is gemaakt van aluminium buizen. Bovenaan het frame is een zeil bevestigd dat dient als afdakje. Daaronder bevindt zich de zitplaats met een rug- en een voetsteun voor de strandwacht. Hieronder is een model van de uitkijktoren getekend.
Van de buizenconstructie is een gedeeltelijk bovenaanzicht gemaakt (zonder zeil, ladder, voet- en rugsteun en opstaande buizen) met de maten daarin in centimeters. Zie de rechterfiguur.

De rechthoeken ABCD, EFGH en PQRS liggen in evenwijdige vlakken.
LM en QR zijn evenwijdig aan BC.
De middens van deze drie rechthoeken liggen recht boven elkaar.

De buizen AK, BL, CM en DN zijn elk 400 cm lang.
De buizen KP, LQ, MR en NS zijn elk 130 cm lang.
De dikte van de buizen wordt in deze opgave verwaarloosd.
2p

10.

 Teken in het bovenaanzicht de opstaande buizen.
De uiteinden van de ladder van de uitkijktoren zijn bevestigd aan de buizen AB en KL.
De ladder is overal even breed en heeft de breedte van KL.
4p

11.

 Bereken de lengte van de ladder

6p

12.

 Bereken de hoek die buis BL met grondvlak ABCD maakt.

De uitkijktoren heeft, afgerond op hele centimeters, een hoogte van 510 cm. Mom de uitkijktoren te demonteren wordt hij gekanteld om ribbe CD zó, dat ribbe RS ook op de grond komt. CD en RS komen dan in ;één horizontaal vlak te liggen. In de figuur hieronder is een aanzicht in de richting van B naar A getekend van de gekantelde uitkijktoren, met hulplijnen die de oorspronkelijke hoogte 510 cm aangeven. Verder zijn er enkele afstanden in centimeters aangegeven.

5p

13.

 Bereken h.

 

Labolift
In een laboratorium maakt men soms gebruik van een zogeheten labolift.
Dit instrument wordt gebruikt om voorwerpen op de juiste hoogte te brengen. Zie de foto.
Via de draaiknop aan de rechterkant van het instrument kan de hoogte van het draagvlak ingesteld worden. In onderstaande figuur zijn twee standen van de labolift in een vooraanzicht schematisch aangegeven.

Lijnstuk AC stelt de onderkant voor en lijnstuk FD stelt het draagvlak voor. Hiertussen bevindt zich een draaibare constructie van metalen strips.
De lijnstukken PS, CT, SQ en TD zijn draaibaar in hun eindpunten en scharnieren in de punten R en U.  Daarbij blijven de punten S en D loodrecht boven C.
Deze vier lijnstukken zijn even lang. R is het midden van zowel lijnstuk PS als lijnstuk TC.
U is het midden van lijnstuk TD en lijnstuk SQ.

Met behulp van de draaiknop kan de afstand tussen T en S worden gevarieerd. Als de afstand TS verandert, verschuiven de punten P en Q in het vooraanzicht:  P schuift van B naar A en van A naar B; Q schuift van E naar F en terug. Hierbij geldt steeds dat PC = TS = QD.
De volgende maten zijn gegeven:
AB = FE = 11 cm,  BC = ED = 4 cm  en  PS = CT = TD = SQ = 16 cm.
5p

14.

 Bereken de kleinst mogelijke afstand tussen A en F.
Geef deze afstand in centimeters. Rond af op één decimaal

De hoek, in graden, tussen RP en PC wordt α genoemd.
3p

15.

 Bereken de kleinste waarde die α kan aannemen.
Geef je antwoord in gehele graden.

Op zeker moment bevindt punt P zich in A.
Aan de draaiknop kan een horizontaal hendeltje bevestigd worden (zie de figuur hiernaast). Hiermee is het mogelijk om de draaiknop met een vaste snelheid rond te draaien. Neem aan dat als gevolg hiervan het punt P met een constante snelheid van 0,3 cm per seconde in de richting van B beweegt.

5p

16.

 Bereken na hoeveel seconden de hoogte van het draagvlak dan gelijk is aan 20 cm.

Nadat er voor gezorgd is dat punt P zich weer in A bevindt, wordt de draaiknop langzamer rondgedraaid zodat P met een constante snelheid van 0,2 cm per seconde in de richting van B beweegt.
Voor de hoogte h, in cm, van het draagvlak geldt de formule:

Hierin is t de tijd in seconden die verstreken is vanaf het moment dat P vanuit punt A in de richting van B beweegt.
In de figuur hiernaast is de grafiek van h getekend en hierin is te zien dat het draagvlak zich vanaf t = 0 steeds langzamer omhoog beweegt. Met behulp van de afgeleide dh/dt kan de bewegingssnelheid van het draagvlak berekend worden.
3p

17.

 Bereken met behulp van differentiëren de formule van dh/dt .

4p

18.

 Onderzoek op welk tijdstip het draagvlak zich met dezelfde snelheid beweegt als het punt P.

Derdegraadsfuncties
Gegeven is de functie  f (x) = -x3 + 27x + 44
De punten A en B zijn de toppen van de grafiek van f.
Zie de bovenste grafiek hiernaast.
Deze toppen liggen even ver van de y-as

5p

19.

 Toon dit aan met behulp van differentiëren.

Q is het snijpunt van de grafiek van f met de y-as. De lijn k door Q  evenwijdig aan de x-as snijdt de grafiek ook nog in de punten P en R. Zie de onderste figuur hiernaast.
5p

20.

 Bereken de lengte van PR.
Rond je antwoord af op twee decimalen.
Een familie van functies is gegeven door h(x) = (x + 4)(p + 4x - x2 ), waarbij p elk reëel getal kan voorstellen.
4p

21.

 Toon aan met behulp van algebra dat er een waarde van p is waarbij de bijbehorende functie h gelijk is aan de functie f.

De grafiek van h heeft twee toppen A en B. Punt A ligt links van de y-as en punt B ligt rechts van de y-as.
Aangetoond kan worden dat de x-coördinaten van deze twee toppen (xA en xB) als volgt afhangen van de waarde van p:
3p

22.

 Bereken algebraïsch voor welke waarde van P geldt dat  xB = 8.

OPLOSSINGEN
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
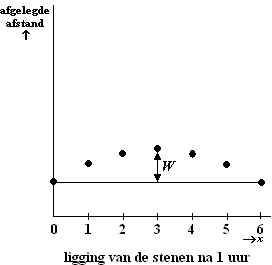
1. Bij steen nummer 2 hoort  x = 2,  en A(2) = -0,1 • 22 + 0,6 • 2 + 19,4 = 20,2 dm
2. -0,1x2 + 0,6x + 19,4 = 20  ⇒  -0,1x2 + 0,6x - 0,6 = 0
ABC formule met a = -0,1 en b = 0,6 en c = -0,6 geeft  x ≈ 1,27 of  x ≈ 4,73
Het dichtst daarbij liggen steen 1 en steen 5 

of

x 0 1 2 3 4 5 6
A(x) 19,4 19,9 20,2 20,3 20,2 19,9 19,4
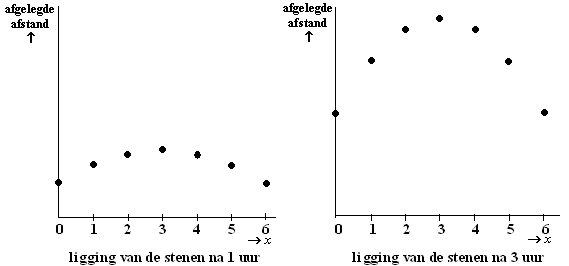
3. A(3) = 20,3 en  A(6) = 19,4 en het verschil daartussen is 0,9 dm = 9cm.
4. per uur neemt het verschil 9 cm toe (zie vraag 3)
voor een verschil van 83 cm is dus  83/9 uur nodig.
Steen 3 legt 203 cm per uur af, dus in 80/9 uur is dat 80/9 • 203 ≈ 1872 cm.
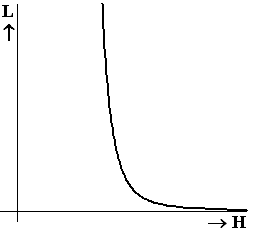
5. d(0) = 3
d(25) = 3 • 0,6725 ≈ 0,00012358...
dat is  3/0,00012358... ≈ 22291 keer zo groot
6. Over de eerste 5 meter is de groeifactor 1,06/5 = 0,212
Bij 15 meter zou dat geven 1,060 • 0,2122 = 0,0476... en dat is inderdaad ongeveer 0,048
7. 1,06 = 5 • e(-2π•5/L)  ⇒  e(-2π•5/L) = 1,06/5 = 0,212  ⇒  -10π/L = ln(0,212) ≈ -1,55
⇒ L = -10π/-1,55 ≈ 20,25306... dus dat is ongeveer 20,25 meter.
8. d =  5 • e -2πx/100  en 0,01 mm is 0,00001 m dus  0,00001 = 5 •  e -2πx/100 
dus   e -2πx/100 = 0,00001/5 = 0,000002
⇒  -2πx/100 = ln(0,000002) ≈ -13,122  ⇒  x ≈ -13,122 • 100/-2π ≈ 208,849
Dus vanaf ongeveer 209 meter.
9. 0,2 = H • e(-20π/L)
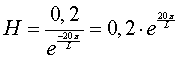
10.
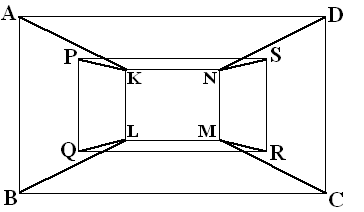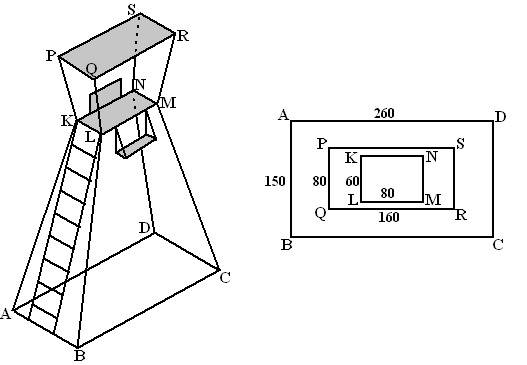
11. Teken ABKL plat. En teken de loodrechte projectie K' van K op AB.
Dan is AK' = 0,5(AB - KL) = 0,5(150 - 60) = 45  en verder is gegeven dat  AK = 400
Pythagoras in AK'K:  4002 = 452 + KK'2  ⇒  KK'= √(4002 - 452 ) = √(157975) ≈ 397 cm.
12. Noem L' de loodrechte projectie van L op het grondvlak.
In het bovenaanzicht is te zien dat  BL'2 = 452 + 902  dus  BL' = √(10125)
In driehoek BLL' geldt dan  cos(ÐL'BL) = BL'/BL = Ö(10125)/400 ≈ 0,25
Dus de gevraagde hoek is  cos-1 (0,25) ≈ 75º 
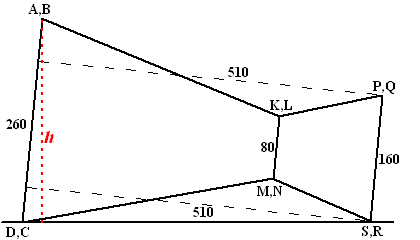
13. Noem R' de projectie van R op ABCD dus in het aanzicht de projectie van R op AD.
Dan geldt  tan ∠RDR' = RR'/ R'D = 510/50  en daaruit volgt dat  ∠RDR' ≈ 84,40066º
Dan geldt  sin 84,40066º = hoogte van B/260  ⇒  hoogte van B = 260 • sin 84,40066º ≈ 259 cm. 
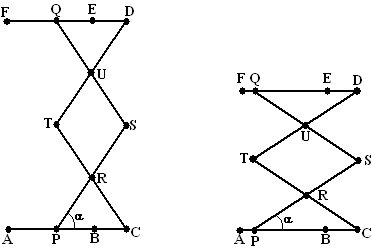
14. De kleinst mogelijk afstand wordt bereikt als punt P zich in A bevindt.
Dan is AC = PC = 15 en verder is AR = RC = 8
Stel dat de hoogtelijn vanuit R op AC in driehoek ACR lengte h heeft
Dan geldt  h2 + 7,52 = 82  ⇒  h = √(82 - 7,52 ) = √7,75
De afstand tussen A en F is 4 keer deze hoogte:  4√7,75 ≈ 11,1 cm
15. α is minimaal als P in A is, dan is in driehoek ACR:  cosα = 7,5/8
Daaruit volgt  α ≈ 20º
16. Als AF 20 is, dan is de hoogte van driehoek ACR gelijk aan 5.
Noem deze hoogtelijn vanuit R op AB dan RR', dan geldt  PR'2 + 52 = 82  ofwel PR' = √(82 - 52 ) = √39
PC is dan 2√39
AP is dan 15 - 2√39 ≈ 2,51
Dat gebeurt dus na 2,51/0,3 ≈ 8,4 seconden.
17.
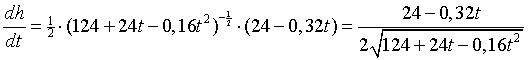
18. Voer in de GR in:
Y1 = √(124 + 24t - 0,16t2 )
Y2 = (Y1(X+ 0,001) - Y1(X))/0,001
Y3 = 0,2
Omdat Y2 nu een benadering is voor dh/dt is de gevraagde t de x-coördinaat van het snijpunt van Y2 en Y3.
Calc - intersect levert  t ≈ 39
19. f '(x) = -3x2 + 27
-3x2 + 27 = 0  ⇒  3x2 = 27  ⇒  x2 = 9  ⇒  x = 3  ∨  x = -3
Dus liggen de toppen even ver van de y-as.
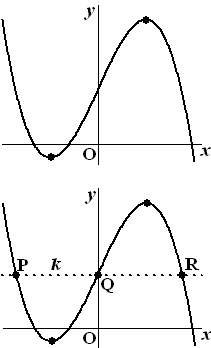
20 x = 0 geeft y = 44 dus k is de lijn y = 44
44 = -x3 + 27x + 44  ⇒  -x3 + 27x = 0  ⇒  x(-x2 + 27) = 0  ⇒  x = 0  ∨  x2 - 27 = 0
⇒  x = 0  ∨  x = √27  ∨ x = -√27
De laatste twee waarden zijn de x-coördinaten van R en P.
De afstand daartussen is 2√27 ≈ 10,39
21. haakjes wegwerken:
xp + 4x2 - x3 + 4p + 16x - 4x2
= -x3 + x(p + 16) + 4p
Daaraan is te zien dat p + 16 = 27  dus p = 11
Als p = 11 is 4p inderdaad ook gelijk aan 44.
22.
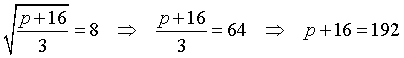
Dus p = 176