HAVO WB12, 2003 - I
Voetstuk
Een pijler onder een brug rust op een betonnen voetstuk. Het voetstuk staat op de grond en bestaat uit twee delen. Het onderste deel heeft de vorm van een balk, het bovenste deel ABCD.EFGHKLMN zorgt voor de overgang naar de pijler die achtzijdig is. Zie de figuur links hieronder
In de figuur rechts is een vooraanzicht van het voetstuk getekend.
In beide figuren zijn de afmetingen gegeven in centimeters.

Met behulp van dit vooraanzicht kan de hoek berekend worden die het schuine vlak BCKH met het vlak ABCD maakt.
5p 1. Bereken die hoek. Rond je antwoord af op gehele graden.

 
In de figuur hieronder is een begin getekend van het bovenaanzicht van het voetstuk op schaal 1 : 10
5p 2. Maak dit bovenaanzicht af. Zet de letters erbij.
Er wordt een lint evenwijdig aan vlak ABCD om het voetstuk gespannen. Het lint is 500 cm lang. Als het lint om het balkgedeelte wordt gespannen is er 100 cm over. Gaat het lint door de punten E, F, G, H, K, L, M en N dan is er ongeveer 283 cm over.
4p 3. Toon met een berekening aan dat er dan inderdaad ongeveer 283 cm over is.

 
Het lint wordt nu op een hoogte van 50 cm (gerekend vanaf de grond) om het voetstuk gespannen.
6p 4. Bereken hoeveel cm van het lint op deze hoogte over is. Rond je antwoord af op een geheel getal.

 
Het gedeelte van het voetstuk tussen de vlakken ABCD en EFGHKLMN wordt geschilderd: de vier vierhoekige zijvlakken worden rood en de vier driehoekige zijvlakken worden zwart. Om te weten hoeveel verf er nodig is moet men de oppervlakte weten.
5p 5. Bereken de totale oppervlakte van de delen die rood geschilderd worden. Rond je antwoord af op gehele cm2.
Medicijnen
Een huisarts schrijft een patiënt een geneesmiddel voor. De patiënt moet dat geneesmiddel enkele weken achtereen gebruiken. Hij neemt één keer per week op maandagochtend één tablet van 500 mg van het medicijn in. De hoeveelheid medicijn in zijn bloed neemt exponentieel af. Na precies één week is nog 30% van de oorspronkelijke hoeveelheid medicijn aanwezig in zijn lichaam.

Uit de gegevens is te berekenen dat de groeifactor per 24 uur ongeveer 0,842 is.
3p 6. Schrijf deze berekening op.

4p 7. Bereken in hoeveel tijd 40% van het toegediende medicijn in zijn lichaam wordt afgebroken. Rond je antwoord af op een geheel aantal uren.

Na inname van een tablet neemt de snelheid waarmee het lichaam van de patiënt het medicijn afbreekt voortdurend af.
5p 8. Bereken de snelheid waarmee zijn lichaam het medicijn 48 uur na inname afbreekt. Geef je antwoord in milligrammen per uur, afgerond op één decimaal.

De patiënt neemt elke week een nieuwe tablet van 500 mg in. We nemen aan dat hij dat steeds na precies een week doet. De hoeveelheid medicijn in zijn lichaam neemt na inname weer exponentieel af met groeifactor 0,842 per 24 uur.
M(t) is de hoeveelheid medicijn in mg in zijn lichaam, t dagen nadat de eerste tablet is ingenomen. In de figuur hieronder is de grafiek van M als functie van t getekend van t = 0  tot  t = 9.
4p 9. Bereken de hoeveelheid medicijn in het lichaam op tijdstip t = 10. Rond je antwoord af op een geheel aantal milligrammen.

4p 10. Stel een formule op voor M(t) voor  14  < t < 21.

Spitsboog
Al heel lang worden in bouwwerken boogconstructies gebruikt om grote ruimten te overspannen. In de figuur hiernaast zie je enkele soorten bogen, waaronder de spitsboog. Een spitsboog is opgebouwd uit twee cirkelbogen. Hierbij ligt het middelpunt ven de ene boog op een uiteinde van de andere cirkelboog.

In de onderste figuur hiernaast is de vorm van een spitsboog OPQ in een assenstelsel getekend. O is het middelpunt van cirkelboog PQ en Q is het middelpunt van cirkelboog OP.

Voor de cirkelboog PQ geldt de volgende formule (met x en h in meter):

h = √(36 - x2)  met  3 ≤ x ≤ 6
3p 11. Bereken de hoogte h van het punt P. Geef je antwoord in twee decimalen nauwkeurig.

We bekijken de grafiek van de functie  h = √(36 - x2) met  -6 ≤ x ≤ 6. De boog PQ is een deel van deze grafiek. Door een ander deel van deze grafiek te verschuiven kan de boog OP van de figuur hierboven verkregen worden. Met behulp van deze verschuiving is een formule voor de boog OP op te stellen.
4p 12. Stel een formule op voor de boog OP. Licht je werkwijze toe.

Een toegangspoort tot een kasteel heeft aan de bovenkant de vorm van een spitsboog en heeft in het vooraanzicht de vorm zoals in de figuur hieronder is afgebeeld. Het gedeelte OPQ in dit vooraanzicht heeft dezelfde afmetingen als in de figuur hierboven. De top P van de spitsboog bevindt zich 8 meter boven de grond.
In het punt P bevindt zich een bewakingscamera. Deze camera neemt niets waar van het gebied onder de raaklijn PT. Het gedeelte RT op de grond in het vooraanzicht valt dus buiten het bereik van deze camera.

Met behulp van de gegeven formule voor de cirkelboog kun je de helling van PT berekenen.
Deze helling is op twee decimalen afgerond -0,58.
4p 13. Bereken met behulp van differentiëren de helling van PT in drie decimalen nauwkeurig.

5p 14. Bereken de lengte van RT. Geef je antwoord in meters. Rond af op één decimaal.

In de figuur hiernaast is de toegangspoort met enkele afmetingen (in m) nogmaals weergegeven.
6p 15. Bereken de oppervlakte van de toegangspoort.
Geef je antwoord in gehele m2.

De functie  f (x) = x • e -x
Gegeven is de functie   f (x) = x • e -x
5p 16. Los op:  -0,1 < f(x)  <  0,1. Rond de getallen in je antwoord af op twee decimalen.

5p 17. Bereken algebraïsch de exacte coördinaten van de top van de grafiek van f.

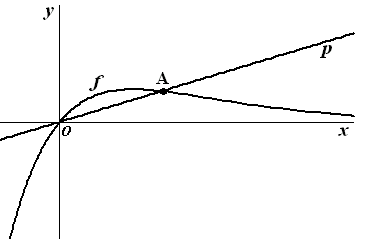
Op de grafiek van  f  ligt rechts van de y-as een punt  A(a , a • e -a). Zie de figuur hieronder.
De lijn p gaat door de punten O(0,0) en A.
De richtingscoëfficiënt van p is 1/4
4p 18. Bereken a.  Rond het antwoord af op drie decimalen.

Een lijn evenwijdig aan de y-as snijdt tussen O en A de grafiek van  f in punt S en de lijn p in punt T.
4p 19. Bereken hoe groot de lengte van ST maximaal is. Rond het antwoord af op drie decimalen.

OPLOSSINGEN
1. De gevraagde hoek is gelijk aan ∠ABH in het vooraanzicht.
Noem P de projectie van H op AB. Dan is  PB = 20 en HB = 40
In driehoek HPB geldt dan  tan(∠ABH) = 40/20  dus  ∠ABH is gelijk aan 63º
2.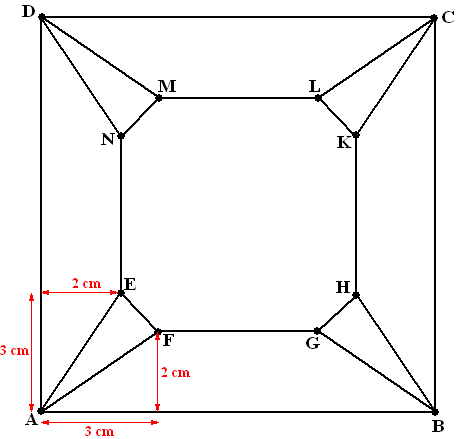
3. GH is de schuine zijde van een rechthoekig driehoekje met rechthoekszijden 10 en 10.
Dus  102 + 102 = GH2  ⇒  GH = √200
De omtrek van EFGHKLMN is dan  4 • 40 + 4 • √200 ≈ 217
Er blijft dan 500 - 217 = 283 cm lint over.
4. 1e opl. De lange zijden van de achthoek nemen af van 100 naar 40 over een hoogteverschil van 40.
Dat is een afname van 60 cm over een hoogte verschil van 40 cm.
Over een hoogte verschil van 10 cm wordt dat dan  1/4 • 60  =15 cm afname.
De lange zijden worden dus 100 - 15 = 85 cm.

De korte zijden nemen toe van 0 naar √200 over een hoogte verschil van 40 cm.
Over een hoogteverschil van 10 cm is dat  1/4 • √200 toename.
De korte zijden worden dus  1/4 • √200

De totale lengte wordt daarmee  4 • 85 + 4 • 1/4 • √200 = 354,142... cm.
Er blijft dan 500 - 354,142... ≈ 146 cm lint over.
2e opl. Op hoogte 40 is het lint 400 cm lang en op hoogte 80 is het lint 217 cm lang.
Dat is een afname van 183 cm over een hoogteverschil van 40 cm.
Over een hoogteverschil van 10 cm geeft dat een afname van  1/4 • 183 = 46 cm.
Het lint wordt dus 400 - 46 = 354 cm lang.
Er blijft dan 500 - 354 = 146 cm lint over.
5. Noem P de projectie van F op vlak ABCD.
In het bovenaanzicht is dan te zien dat  PA2 = 202 + 302  dus  PA = √1300
In driehoek  PAF is dan te zien  AF2 = PF2 + AP2 = 402 + 1300 = 2900  dus  AF = √2900
Teken nu vlak ABGF en noem Q de projectie daarin van F op AB.
Dan geldt  FQ2 = AF2 - AQ2 = 2900 - 302 = 2000  dus  FQ = √2000
ABGF valt uiteen in twee driehoeken en een rechthoek.
De oppervlakte O is dan:  O = 2 • driehoek + rechthoek = 2 • 0,5 • 30 • √2000 + 40 • √2000 = 70 • √2000
Er zijn 4 zulke vlakken dus de totale rode oppervlakte wordt  4 • 70 • √2000 ≈ 12522 cm2
6. De groeifactor per week is  0,3
Een week is 7 perioden van 24 uur.
Als g de groeifactor per periode van 7 uur is, dan geldt dus  g7 = 0,3  dus  g = 0,31/7 = 0,841982...
7. Als 40% wordt afgebroken is nog 60% over. Dat is  0,6 • 500 = 300 mg
Er moet dus gelden  300 = 500 • 0,842t  ⇒  0,842t = 0,6  ⇒  t = 0,842log 0,6 = (log 0,6)/log(0,842) = 2,970
Dat is  2,970 • 24 = 71 uur.
8. 1e opl. De formule bij dit proces is  M(t) = 500 • 0,842t.  (M = hoeveelheid in het lichaam)
De snelheid van verandering is de afgeleide:  M'(t) = 500 • 0,842t • ln(0,842)
Op tijdstip t = 2 geldt  M'(2) = -60,966...mg/dag
Dat is  24 • -60,966... ≈ -2,5 mg/uur
2e opl. De formule bij dit proces is  M(t) = 500 • 0,842t.  (M = hoeveelheid in het lichaam)
Voer deze formule in bij Y1 in de GR, en gebruik CALC  - dy/dx  om de snelheid te vinden.
Dat geeft -60,966...mg/dag en dat is  24 • -60,966... ≈ -2,5 mg/uur
9. Na de eerste week is nog  500 • 0,3 = 150 mg over.
Na inname van de tweede tablet is er 500 + 150 = 650 mg. Dat wordt vervolgens nog 3 dagen lang afgebroken.
De hoeveelheid wordt dan  650 • 0,8423 ≈ 388 mg medicijn.
10. 1e opl. Na de eerste week is nog  500 • 0,3 = 150 mg over. Daar komt 500 mg van de tweede tablet bij.
Na de tweede week is 650 • 0,3 = 695 mg over.
Dat wordt vanaf t = 14 afgebroken
De formule wordt daarom  M(t) = 695 • 0,842t- 14
2e opl. Van de eerste tablet is nog  500 • 0,842t over
Van de tweede tablet is nog  500 • 0,842t - 7 over
Van de derde tablet is nog  500 • 0,842t - 14 over
In totaal is er M(t) = 500 • (0,842t + 0,842t - 7 + 0,842t -14) over
11. De x- coördinaat van P is 3.
h(3) = √(36 - 32) = √27 ≈ 5,20
12. De formule  h = √(36 - x2) beschrijft een halve cirkel.
Als je het stuk tussen x = -6 en x = -3  zes naar rechts schuift, dan krijg je precies  boog OP
Zes naar rechts schuiven betekent voor de formule  x vervangen door x - 6
De formule wordt dus  h = √(36 - (x - 6)2)  voor  0 ≤ x ≤ 3
13. h(x) = (36 - x2)1/2 dus  (met de kettingregel):  h '(x) = 1/2 • (36 - x2) -1/2 • -2x
De helling in het punt waar x = 3 is h '(3) ≈ -0,577
14. Over PT ga je bij 1 naar rechts  0,577 omlaag. Dus bij 8 omlaag ga je  8/0,577 ≈ 13,9 naar rechts.
De afstand van het midden van RS tot T is dus 13,9, dus de afstand RT = 13,9 - 3 = 10,9 meter.
15.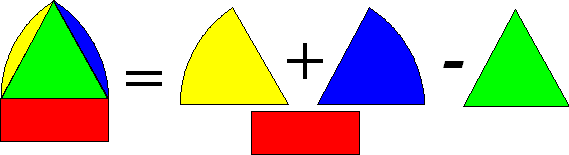
De spitsboog is te zien als een rechthoek plus twee cirkelsegmenten min een gelijkzijdige driehoek.
De rechthoek heeft oppervlakte  2,8 • 6 = 16,8 m2.
Een cirkeldeel is 1/6 van een hele cirkel met straal 6, dus de oppervlakte is  1/6 • π • 62 = 6π
Samen zijn beide cirkeldelen dus  12π
Teken de hoogtelijn h in de gelijkzijdige driehoek, dan geeft Pythagoras:  h2 = 62 - 32 = 27  dus  h = √27
De oppervlakte van de driehoek is dus  0,5 • 6 • √27 = 3√27
Daarmee wordt de gevraagde oppervlakte  16,8 +  12π - 3√27 ≈ 39 m2
16. Voer de functie f  en de lijnen y = -0,1 en y = 0,1 in in de GR.
Gebruik INTERSECT om de snijpunten te vinden. Dat geeft  x = 0,11 en x = 3,58 en x = -0,09
Lees vervolgens af waar de grafiek van f tussen beide lijnen in ligt.
Dat is zo voor  -0,09 < x < 0,11  of  x > 3,58
17. Met de productregel en de kettingregel:
f '(x) =  1 • e-x + x• e-x • -1 = e-x • (1 - x)
Voor de top geldt  f '(x) = 0  dus  e-x • (1 - x) = 0  en dat is zo als  x = 1
f (1) = 1 • e-1 = 1/e de top is dus het punt  (1 , 1/e)
18. A is het snijpunt van de lijn  y = 0,25x  met   f(x) = x • e-x  dus moet gelden  0,25x =  x • e-x   ofwel  e-x = 0,25
e-x = 0,25 ⇒  -x = ln(0,25)  ⇒  x = -ln 0,25 = ln 4 ≈ 1,386
19. De lengte ST is gelijk aan  x • e -x  - 0,25x (het verschil van beide y -coördinaten)
Voer deze vergelijking in in de GR en bereken met CALC - Maximum de maximale waarde van ST.
Dat geeft  x ≈ 0,562 en een maximum van STMAX » 0,180