Nieuwe pagina 1

OPGAVE 1. Misdrijven.

Elk jaar worden in Nederland veel misdrijven gemeld. Deze variëren van het stelen van een chocoladereep tot het plegen van een moord. Misdrijven worden gemeld bij het Openbaar Ministerie (OM). Het OM beslist dan over de (eventuele) vervolging van de daders. In de volgende figuur vind je informatie over misdrijven die in 1996 werden gemeld.



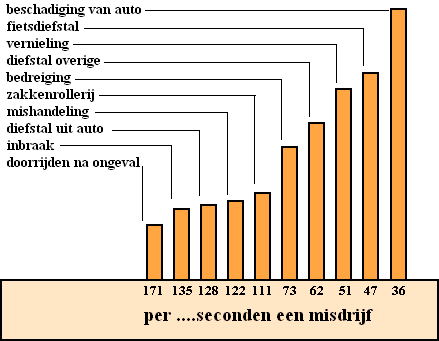
De getallen langs de horizontale as geven voor elke categorie aan hoeveel seconden er gemiddeld tussen twee opeenvolgende meldingen zitten. Je kunt bijvoorbeeld aflezen dat in 1996 in Nederland (gemiddeld) elke 135 seconden een inbraak werd gemeld. Let op: 1996 was een schrikkeljaar en had dus 366 dagen. In de figuur komt ook de categorie 'fietsdiefstal' voor.

4p.	1.	Toon aan dat er in 1996 ongeveer 670000 keer een fietsdiefstal werd gemeld.

Als je de staafjes en de getallen in de figuur bekijkt, dan zie je:

•	van links naar rechts zijn de getallen steeds kleiner
•	van links naar rechts zijn de staafjes steeds langer.

3p.	2.	Leg uit hoe uit de getallen kan worden afgeleid dat een langere staaf bij een groter aantal misdrijven hoort.

In drie van de tien categorieën misdrijven komt het woord diefstal voor, namelijk: 'fietsdiefstal', 'diefstal overige' en 'diefstal uit auto'. Je kunt deze drie categorieën samenvoegen tot één (nieuwe) categorie 'diefstal'. Je moet dan de drie bijbehorende staafjes vervangen door één (nieuwe) staaf. Onder deze nieuwe staaf 'diefstal' moet dan ook weer een getal staan.

4p.	3.	Bereken welk getal onder deze nieuwe staaf 'diefstal' moet staan.

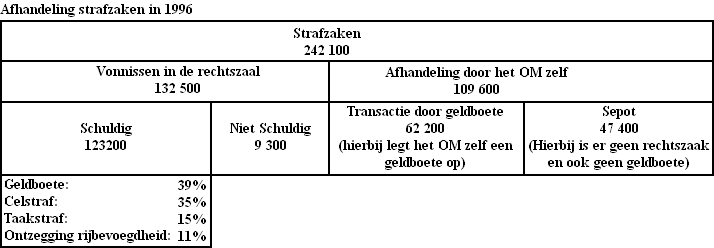
Bij veel gemelde misdrijven is er geen verdachte aangewezen. Is er gaan verdachte, dan komt er ook geen strafzaak. In 1996 werden er door het OM 242100 strafzaken afgehandeld. In de onderstaande tabel vind je informatie over de manier waarop die afhandeling plaatsvond.



4p.	4.	Bereken hoeveel procent van alle 242100 strafzaken tot een geldboete leidde.

Het aantal strafzaken dat het OM met een transactie afhandelt groeit elk jaar fors. In 1990 werden 50 000 strafzaken met een transactie afgehandeld. In 1996 waren dat er al 62 200. Neem aan dat het aantal strafzaken dat met een transactie wordt afgehandeld elk jaar met het zelfde percentage groeit.

5p.	5.	Bereken dit percentage.

OPGAVE 2. Sporttesten.

Bij veel sporten speelt explosieve kracht een belangrijke rol. Denk bijvoorbeeld aan basketbal en tennis.
Bij geschiktheidstesten voor dit soort sporten moet de persoon die getest wordt (op commando) vanuit stilstand zo hoog mogelijk springen. Met zo'n verticale sprong meet men de spronghoogte.

Een meisje wil graag uitverkozen worden voor de basketbalselectie. Zij moet daarvoor in elk geval een spronghoogte van 60 cm kunnen bereiken. Zij heeft veel geoefend. Soms haal;de zij die 60 cm wel, maar meestal niet.
Haar spronghoogte is (bij benadering) normaal verdeeld met een gemiddelde van 56 cm en een standaardafwijking van 6 cm.

5p.

Bereken in hoeveel procent van haar sprongen de spronghoogte 60 cm of meer is.

Met de tabellen hieronder kun je - in twee stappen - bepalen hoeveel punten een bepaalde spronghoogte oplevert voor de geschiktheidstest van een kandidaat:

•

In tabel 1 kun je de score aflezen die spronghoogte h (in cm) oplevert bij een lichaamsgewicht van g (in kg)

•

In tabel 2 zijn de scores (afzonderlijk voor mannen en vrouwen) omgerekend in punten.

TABEL 1		gewicht g
TABEL 1		30	35	40	45	50	55	60	65	70	75	80	85	90
spronghoogte h	20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100	53 67 80 93 107 120 133 147 160 173 187 200 213 227 240 253 267	60 75 90 105 120 135 150 165 180 195 210 225 240 255 270 285 300	67 83 100 117 133 150 167 183 200 217 233 250 267 283 300 317 333	73 92 110 128 147 165 183 202 220 238 257 275 293 312 330 348 367	80 100 120 140 160 180 200 220 240 260 280 300 320 340 360 380 400	87 108 130 152 173 195 217 238 260 282 303 325 347 368 390 412 433	93 117 140 163 187 210 233 257 280 303 327 350 373 397 420 443 467	100 125 150 175 200 225 250 275 300 325 350 375 400 425 450 475 500	107 133 160 187 213 240 267 293 320 347 373 400 427 453 480 507 533	113 142 170 198 227 255 283 312 340 368 397 425 453 482 510 538 567	120 150 180 210 240 270 300 330 360 390 420 450 480 510 540 570 600	127 158 190 222 253 285 317 348 380 412 443 475 507 538 570 602 633	133 167 200 233 267 300 333 367 400 433 467 500 533 567 600 633 667

TABEL 2. Scores		Punten
Mannen	Vrouwen	Punten
360 en hoger 342 en hoger 324 en hoger 307 en hoger 289 en hoger 271 en hoger 253 en hoger 236 en hoger 218 en hoger 200 en hoger	220 en hoger 207 en hoger 193 en hoger 180 en hoger 167 en hoger 153 en hoger 140 en hoger 127 en hoger 113 en hoger 100 en hoger	15 13,5 12 10,5 9 7,5 6 4,5 3 1,5

3p.

Geef in tabel 1 aan bij welke combinaties van spronghoogte en gewicht het maximale aantal van 15 punten door mannen behaald wordt. Licht je antwoord toe.

Als je tabel 1 bekijkt zie je dat de scores per rij en ook per kolom regelmatig oplopen (op afrondingen na). Om dit duidelijker te zien is een deel van de tabel eruit gehaald. Zie de volgende tabel 3.

TABEL 3		gewicht g
TABEL 3		30	40	50	60	100
sprong- hoogte h	30 60 90 120	80 160 240 ...	100 200 300 ...	120 240 360 ...	140 280 420 ...	... ... ... ...

5p.

Vul de acht ontbrekende scores in. Gebruik hierbij de regelmaat in de tabel.

We gaan formules bij tabel 3 maken.
Bij de rij met h = 30 past een formule als: score = 2(g - 30) + 80 of score = 2g + 20
Bij de rij met h = 60 past een formule als: score = 4(g - 30) + 160 of score = 4g + 40

4p.

Stel een formule op die past bij de rij met h = 90 en toon aan dat die formule juist is.

Tabel 1 geeft slechts scores voor lichaamsgewichten tot en met 90 kg.
Je kunt tabel 1 uitbreiden voor grotere lichaamsgewichten.
Een forse basketballer heeft een spronghoogte van 45 cm. Volgens een uitgebreide tabel 1 en tabel 2 krijgt hij daarvoor 15 punten.

4p.

10.

Hoeveel kg weegt deze basketballer minstens? Licht je antwoord toe.

OPGAVE 3. De kleurenblinde en de glasbak.

Ongeveer een half miljoen Nederlanders is kleurenblind. Een kleurenblinde ziet (bijna) geen verschil tussen (bepaalde) kleuren. Gekleurde flessen zijn groen of bruin. Sommige kleurenblinden zien geen verschil tussen groen en bruin. Zij staan met hun lege flessen voor de glasbak en weten niet of ze een gekleurde fles in het gat voor groen glas of in het gat voor bruin glas moeten gooien.



Peter is kleurenblind. Hij kan de groene en de bruine flessen niet van elkaar onderscheiden. Als Peter met zijn lege flessen bij de glasbak komt, gooit hij de witte flessen altijd in het juiste gat. Bij een gekleurde fles kiest hij aselect tussen het gat voor groen en het gat voor bruin. De kans dat een groene of bruine fles in het goede gat terechtkomt is dus 0,5.
Het kan gebeuren dat Peter alle gekleurde flessen toevallig in het goede gat gooit. Hij denkt: "Hoe meer gekleurde flessen ik heb, hoe kleiner de kans dat ik alle gekleurde flessen in het goede gat gooi"

3p.	11.	Laat met een getallenvoorbeeld zien dat deze gedachte juist is.

Peter brengt 100 lege flessen naar de glasbak. De helft van zijn flessen is van wit glas. Bij de andere helft zijn zowel groene als bruine flessen.

3p	12.	Laat zien dat naar verwachting 75 van de 100 flessen in het goede gat terechtkomen.

Uit vraag 12 volgt: de kans dat een fles in het goede gat terechtkomt als Peter de witte flessen altijd goed gooit en bij elke gekleurde fles aselect kiest tussen het gat voor groen en het gat voor bruin. Uit onderzoek is gebleken dat van de lege flessen in de glasbak 50% wit, 40% groen en 10% bruin is. Neem aan dat dit ook voor de flessen van Peter geldt. Je kunt het gooien van de flessen in de glasbak weergeven met een boomdiagram. Zie volgende figuur



Peter kan de kans dat hij een fles in het goede gat gooit hoger krijgen dan 75%. Hij gooit de witte flessen allemaal in het goede gat. Hij concludeert uit het onderzoek dat van de gekleurde flessen ⁴/₅ deel groen is en ¹/₅ deel bruin. In die verhouding gaat hij de flessen in de gaten gooien. Elke gekleurde fles heeft dan ⁴/₅ kans om in het gat voor groen terecht te komen en ¹/₅ kans om in het gat voor bruin terecht te komen.

7p.	13.	Bereken voor deze werkwijze de kans dat een willekeurige fles in het goede gat terechtkomt.

Er bestaan nog betere werkwijzen voor Peter. In zo'n werkwijze is de kans dus nog groter dat een fles in het goede gat terechtkomt.

5p.	14.	Geef een voorbeeld van zo'n werkwijze en toon aan dat deze beter is.

OPGAVE 4. De klokjesgentiaan.

De klokjesgentiaan (zie foto) kwam vroeger veel voor op vochtige heidegebieden. Het is een meerjarig, zaaddragend plantje. Uit het zaad ontstaan in het voorjaar kiemplantjes.

Tijdens de ontwikkeling van het plantje onderscheiden we drie fasen:

•

kiemplantje (fase K)

•

niet-bloeiend plantje (fase N) en

•

bloeiend plantje (fase B)

We laten het zaad (en de zaadverspreiding) buiten beschouwing; er ontstaan dus geen nieuwe kiemplantjes.

In een proefveld is onderzoek gedaan naar de ontwikkeling van deze plantjes. De volgende matrix geeft een redelijk goede beschrijving van de jaarlijkse ontwikkeling.

Zo lees je bijvoorbeeld af dat 48% van de kiemplantjes een jaar later bloeiende plantjes zijn geworden.

In het voorjaar van 1996 zijn 1000 kiemplantjes in het proefveld uitgezet.

4p.

15.

Leg uit dat er volgens jet matrixmodel na enkele jaren alleen nog maar bloeiende plantjes zijn.

8p.

16.

Bereken met dit matrixmodel in welk jaar het aantal bloeiende plantjes voor het eerst kleiner is dan 175.

In 2002 worden op een proefveld 71 kiemplantjes uitgezet. Met behulp van de matrix kan worden berekend dat er een jaar later 4 plantjes in fase N en 34 plantjes in fase B zijn. De overige 33 plantjes zijn doodgegaan. Deze getallen zijn al ingevuld in onderstaand schema.
Uitgaande van die aantallen 4 en 34 kan met behulp van de matrix de situatie in 2004 en verder worden berekend. Bij die berekeningen worden de aantallen elk jaar op gehelen afgerond en wordt met die afgeronde getallen verder gerekend.

	K	N	B
2002	71	0	0
2003	0	4,26 = 4	34,08 = 34
2004	0	0	....
2005	0	0	....
2006	-0	0	....

5p.

17.

Vul het schema in; maak daarbij gebruik van gegevens uit de matrix. Licht je werkwijze toe.

OPGAVE 4. De Rede van Veere.

In de zeventiende eeuw was de fluit een veel voorkomend scheepstype. In het stadhuis van Veere hangt een schilderij "De rede van Veere" uit 1651 waarop maar liefst 14 fluiten staan. naast het schilderij hangt een lijst met onder andere de lengte en het laadvermogen van elk van deze fluiten.


bron: Museum De Vierschaar te Veere

Er waren twee soorten fluiten: de Amsterdamse fluit en de Rotterdamse fluit. Van beide soorten is bekend dat de afmetingen niet altijd hetzelfde waren. Bij de Amsterdamse fluiten was er een vaste verhouding tussen lengte, breedte en hoogte. Je kunt dus zeggen dat alle Amsterdamse fluiten een vergroting of verkleining van elkaar waren. ook bij de Rotterdamse fluiten was er een vaste verhouding tussen lengte, breedte en hoogte, maar die verhouding was anders dan bij de Amsterdamse fluiten. Een grotere fluit kan meer lading vervoeren. Zo zijn bij een twee keer zo lange fluit ook breedte en hoogte twee keer zo groot. Dus is de inhoud dan acht keer zo groot. Het laadvermogen is evenredig met de inhoud van de fluit. Dus is het laadvermogen evenredig met de derde macht van de lengte. In onderstaande figuur is het laadvermogen uitgezet tegen de derde macht van de lengte; om grote getallen te vermijden is (langs de horizontale as) lengte³ gedeeld door 10000. Elke stip stelt een fluit voor. De lengte is in voeten (1 voet ≈ 30 cm) en het laadvermogen is in lasten (1 last ≈ 2000 kg).



In deze figuur ontbreekt een fluit van het schilderij. Deze had een lengte van 109 voet en een laadvermogen van 130 last.

4p.	18.	Was dit een Amsterdamse of een Rotterdamse fluit? Licht je antwoord toe.

Met behulp van deze figuur zijn formules af te leiden waarmee het laadvermogen van Amsterdamse en Rotterdamse fluiten berekend kan worden:


Voor Amsterdamse fluiten geldt: c = 1

4p.	19.	Bereken c in de formule voor het laadvermogen van Rotterdamse fluiten.

Twee fluiten op het schilderij hadden dezelfde naam: De Hoope. De ene had een laadvermogen van 120m last en was 100 voet lang. De andere had ook een laadvermogen van 120 last, maar had een grotere lengte.

6p.	20.	Bereken het lengteverschil van deze twee fluiten. Geef je antwoord in hele voeten.

UITWERKING

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

HAVO WA (oude stijl), 2001 - I