HAVO WA, 1997 - I

 

OPGAVE 1. Benzineprijzen in Europa.
       
Een liter benzine kost niet in ieder land evenveel. in een voorlichtingsfolder van de ANWB werden prijsverschillen van juni 1995 in een tabel vermeld. Zie de volgende tabel. Alle bedragen zijn omgerekend in guldens.
       
Waar is benzine goedkoper?
Grensovergang goedkoper in gld/liter voordeel
Nederland/België
Belgie/Luxemburg
Luxemburg/Frankrijk
België/Frankrijk
Frankrijk/Spanje
Nederland/Duitsland
Duitsland/Oostenrijk
Duitsland/Zwitserland
Oostenrijk/Italië
Zwitserland/Italië		 België
Luxemburg
Luxemburg
België
Spanje
Duitsland
Oostenrijk
Zwitserland
Oostenrijk
Zwitserland		 0,17
0,33
0,48
0,15
0,44
0,05
0,19
0,25
0,09
0,15
       
Het prijsvoordeel in deze tabel is gebaseerd op Eurosuper (loodvrij 95)

In onderstaande graaf zijn de grensovergangen van de negen genoemde landen aangegeven.
       

       
Bij de overgang  NL/België is de benzine in België f 0,17 per liter goedkoper. In de graaf geef je dat aan met een pijl en een bedrag:  

       
5p. 1. Geef in de graaf de gegevens van de grensovergangen die in de tabel zijn genoemd aan.
       
6p. 2. Zet in de graaf de juiste pijlen en bedragen bij de resterende grensovergangen.
       
In juni 1995 kostte een liter benzine in Nederland f 1,90.
       
6p. 3. Noem de drie landen met de laagste benzineprijzen en vermeld bij elk van deze landen de prijs per liter.
       
OPGAVE 2.  Hepatitis A.
         
Hepatitis A wordt in het algemeen gezien als een onschuldige infectieziekte, maar sommige mensen kunnen van Hepatits A ernstig ziek zijn.
Het lichaam kan antistoffen maken tegen het Hepatits A-virus. Is dat bij iemand gebeurd, dan is hij immuun. Dat wil zeggen dat hij deze ziekte niet meer kan krijgen.
Met een AHA-test kan worden vastgesteld of iemand antistoffen heeft. Zonder antistoffen is hij niet immuun en loopt hij het risico van besmetting.
In de volgende figuur is voor elke leeftijd af te lezen hoeveel procent van de Nederlandse bevolking (van die leeftijd) niet immuun is voor het Hepatitis A-virus.
         

         
Voor de Nederlandse bevolking geldt dat het percentage 45-jarigen dat immuun is ruim drie keer zo groot is als het percentage 30-jarigen
         
4p. 4. Leg met behulp van de figuur uit dat dit klopt.
         
In de tropen is het risico van besmetting door het Hepatitis A-virus groot voor mensen die niet immuun zijn. Nederlanders die naar de tropen reizen kunnen zich laten inenten. Hierdoor zijn ze tijdelijk immuun voor Hepatitis A.
De gezondheidsdienst kan kiezen tussen twee procedures:
1. 'Blind inenten'; dat wil zeggen dat iedere tropenreiziger wordt ingeënt. Er wordt niet vooraf onderzocht of hij al immuun is voor Hepatitis A.
2. 'Gericht inenten'; dat wil zeggen dat iedere tropenreiziger eerst een AHA-test ondergaat. Is de reiziger niet immuun dan wordt hij ingeënt, anders wordt hij niet ingeënt.
         
Neem aan dat een inenting f 200,- per persoon kost en een AHA-test f 40,-.
We bekijken een groep van 20 aselect gekozen Nederlanders van dezelfde leeftijd die naar de tropen willen reizen. Er zijn nu twee mogelijkheden: 'blind inenten' of 'gericht inenten'.

Stel dat al deze mensen 50 jaar oud zijn.
         
6p. 5. Laat met een berekening zien dat 'gericht inenten' voor deze groep naar verwachting goedkoper in dan 'blind inenten'.
         
Bij een andere leeftijd dan 50 jaar zijn voor zo'n groep van 20 mensen de verwachte kosten van 'gericht inenten' gelijk aan de kosten van 'blind inenten'.
         
6p. 6. Welke leeftijd is dat? Licht je antwoord toe.
         
Uit de figuur kunnen ook kansen worden afgeleid. Zo is bijvoorbeeld de kans dat een willekeurige Nederlander van 25 jaar niet immuun is, gelijk aan 0,92.
         
4p. 7. Bereken met behulp van de figuur de kans dat van een groep van 20 aselect gekozen Nederlanders van 60 jaar iedereen immuun is, zodat niemand ingeënt hoeft te worden.
         
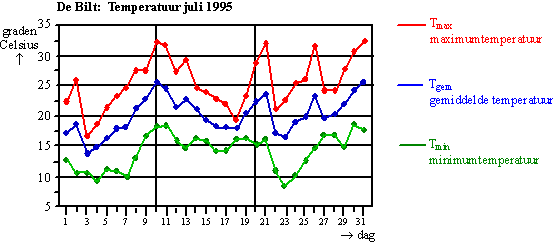
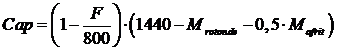OPGAVE 3.  Rotonde.
         
Momenteel worden veel kruispunten vervangen door rotondes.
Het is niet verstandig om van elk kruispunt een rotonde te maken. Als er teveel verkeer van zo'n rotonde gebruik gaat maken, zullen er opstoppingen ontstaan. Het is dan beter om andere maatregelen te nemen zoals het plaatsen van verkeerslichten. Als men overweegt om op een bepaald kruispunt een rotonde aan te leggen, laat men daarom eerst verkeerstellingen doen.
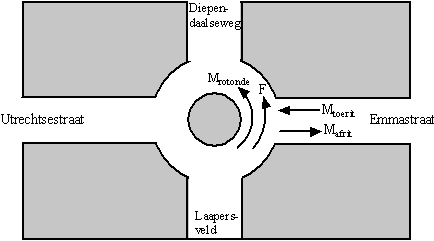
Bij het kruispunt Emmastraat/Diependaalseweg/Utrechtsestraat/Laapersveld zijn die tellingen gehouden op een aantal werkdagen tussen 8:00 en 9:00 uu, de periode waarin het daar het drukst is.

Als men doet alsof er op dit kruispunt al een rotonde is aangelegd, kunnen aan de hand van de tellingen voor elk van de vier wegen de volgende gegevens worden berekend:
F: het aantal fietsers dat op de rotonde de betreffende weg voorbijrijdt
Mrotonde het aantal motorvoertuigen dat op de rotonde de betreffende weg voorbijrijdt.
Mafrit het aantal motorvoertuigen dat de rotonde over de betreffende weg verlaat.
Mtoerit het aantal motorvoertuigen dat de rotonde over de betreffende weg oprijdt.
         
Alle aantallen in deze opgave zijn per uur.
         

         
Hierna wordt voor elke weg de zogenaamde capaciteit Cap berekend, met de formule:
         

         
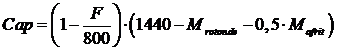Deze capaciteit van een weg is het maximale aantal motorvoertuigen dat per uur over deze weg de rotonde kan oprijden zonder dat er opstoppingen ontstaan.
Voor de Emmastraat zijn de volgende gegevens bekend:
F = 309,  Mrotonde = 107,  Mafrit = 217,  Mtoerit = 730
         
4p. 8. Onderzoek of voor de Emmastraat geldt dat Mtoerit kleiner is dan Cap
         
Verkeersdeskundigen hanteren als regel dat een rotonde mogelijk is als voor ieder van de wegen naar de rotonde geldt:  Mtoerit ≤ Cap.
Voor de Utrechtsestraat geldt Mrotonde = 120, Mafrit = 303, Mtoerit = 534.
         
6p. 9. Bereken voor de Utrechtsestraat voor welke waarden van F nog geldt dat Mtoerit ≤ Cap.
         
We bekijken een andere kruising (zie onderstaande figuur). Men wil onderzoeken of het mogelijk is om hier een rotonde aan te leggen. Op deze kruising van Appelweg (A), Bessenweg (B), Citroenweg (C) en Druivenweg (D) mogen geen fietsers rijden. Ook nu heeft men op werkdagen gedurende het drukste uur van de dag het aantal motorvoertuigen geteld. Zie de onderstaande tabel.
         

         
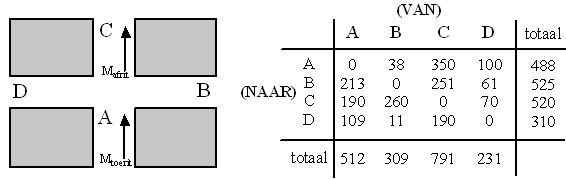In de tabel lees je bijvoorbeeld af dat van alle auto's die over weg A de kruising opreden, er 213 via weg B de kruising weer verlieten.
Ook hier doet men alsof er al een rotonde is aangelegd.
         
4p. 10. Lees uit de tabel af hoe groot Mtoerit van weg A en Mafrit van weg C zijn.
         
Als van een weg Mafrit en Mrotonde bekend zijn, kunnen we de capaciteit Cap schatten met behulp van onderstaande figuur.
Zo is bijvoorbeeld af te lezen dat als Mafrit  = 500 en Mrotonde = 250, Cap ongeveer 940 is.
         

         
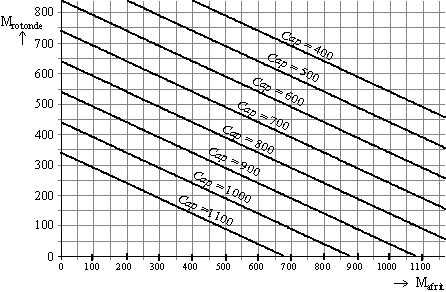Deze kruising kan door een rotonde worden vervangen als als ook hier voor elk van de vier wegen geldt dat Mtoerit ≤ Cap.
Voor de wegen A, C en D is dit al vastgesteld. Uit de bovenstaande tabel kunnen Mtoerit en Mafrit voor weg B worden afgelezen.
Voor weg B is bekend dat Mrotonde = 369.
         
5p. 11. Onderzoek met behulp van de grafieken hierboven of ook voor weg B geldt dat Mtoerit ≤ Cap. Licht je werkwijze toe.
         

 

OPGAVE 4.  Lengteverdeling van jongens.
         
Er is onderzoek gedaan naar de lichaamslengte van jongens van 3 tot en met 20 jaar. Voor elke leeftijd werd de lengte van een groot aantal jongens gemeten. In de volgende figuur staan de resultaten van het onderzoek.
         

         
Voor elke leeftijdsgroep werden P3, P10, P50, P90 en P97 bepaald.
De drie-percentiel (P3) van een groep is de lengte L waarvoor geldt dat 3% van de jongens van die groep kleiner is dan L. Zo kun je ook P10, P50, P90 en P97 omschrijven.
Een voorbeeld:  voor jongens van 9 jaar geldt P90 = 144 cm (zie de figuur) Dat betekent dat 90% van de 9-jarige jongens kleiner is dan 144 cm.

Stel dat voor elke leeftijd de lengte van de jongens normaal verdeeld is. Dan is uit bovenstaande figuur af te leiden dat de standaardafwijking van de lengte niet voor elke leeftijd even groot is.
         
3p. 12. Voor welke leeftijd is de standaardafwijking het grootst? Licht je antwoord toe.
         
Voor 18-jarige jongens geldt dat de gemiddelde lengte 181 cm is en de standaardafwijking 6,7 cm. Stel dat voor 18-jarige jongens de lengte normaal verdeeld is.
         
6p. 13. Bereken P97 voor 18-jarige jongens en controleer of dit in overeenstemming is met de figuur.
         
Bij iedere leeftijd zullen gemiddelde lengte en standaardafwijking anders zijn. Stel dat voor 21-jarige jongens geldt dat hun lengte normaal verdeeld is en dat P10 = 174 cm en P90 = 190 cm.
         
6p. 14. Bereken de standaardafwijking van de lengte van de 21-jarige jongens.
         

 

OPGAVE 5. Het weer in juli 1995.
         
Juli 1995 was een maand met uitzonderlijk mooi weer. Onderstaande tekst en figuren zijn ontleend aan een artikel in het tijdschrijft Zenith.
         
Met in de Bilt en gemiddelde temperatuur van 20,1 ºC komt juli 1995 op een tweede plaats in de rij van warme julimaanden van deze eeuw.
In juli 1995 werd werd op zes dagen de grens van 30,0 ºC bereikt of overschreden (tropische dagen); normaal is dat op één dag het geval.
Er werden 15 zomerse dagen (maximumtemperatuur tenminste 25,0 ºC) genoteerd tegen zes normaal. De grens van 20,0 ºC (warme dagen) werd op 28 dagen overschreden; normala gebeurt dat op 18 dagen.
Juli was een zeer zonnige maand. De Bilt registreerde 256 uren zon tegen een normale waarde van 187 uren. Zonloze dagen kwamen er niet voor; het gemiddelde over het tijdvak 1961 -1990 is twee.
         

         

         
In de onderste figuur is bijvoorbeeld af te lezen dat op 1 juli de zon 10 uur scheen terwijl de daglengte 16,8 uur was.

Er waren dagen in juli 1995 waarop de zon weinig scheen (minder dan 5 uur) en het toch warm was (maximumtemperatuur meer dan 20ºC)
         
3p. 15. Geef een voorbeeld van zo'n dag.
         
In het artikel staat dat er 15 dagen waren met een maximumtemperatuur van 25ºC of meer. Dat is ook in de bovenste grafiek af te lezen. Hieruit volgt dat de mediaan van de maximumtemperatuur van deze maand juli iets onder de 25ºC moet liggen.
         
6p. 16. Maak met behulp van de gegevens uit de bovenste figuur een boxplot van Tmax, de maximumtemperaturen van de dagen van deze maand. Licht je werkwijze toe.
         
De gemiddelde temperatuur Tgem van een dag ligt vaak ongeveer midden tussen Tmax en Tmin van die dag in.
Op 22 juli is dat duidelijk niet het geval. Zie de bovenste figuur.
Met de drie gegevens Tmin, Tgem en Tmax is natuurlijk niet te achterhalen hoe het temperatuurverloop op die dag precies was.
In de figuur hieronder zijn drie mogelijke temperatuurverlopen getekend. Met behulp van de gegevens uit de bovenste figuur kunnen we vaststellen welke het temperatuurverloop van 22 juli 1995 zou kunnen zijn.
         

         
5p. 17. Geef van elk van de drie grafieken aan of deze het temperatuurverloop op 22 juli kan weergeven. Licht je antwoorden toe.
         
De daglengte is de tijd tussen zonsopkomst en zonsondergang. In de grafiek met het aantal uren zonneschijn is aan de lengte van de staven te zien dat de daglengte afneemt van 16,8 uur aan het begin van de maand naar 15,5 uur aan het eind.
Als deze afname zich gelijkmatig zou voortzetten kan hieruit de daglengte op 21 december, de kortste dag, berekend worden.
         
5p. 18. Is de uitkomst van deze berekening gelijk aan 7,7 uur, de werkelijke daglengte op 21 december? Licht je werkwijze toe.
         
UITWERKING
   
1.  
   
2.  
   
3.  
   
4.  
   
5.  
   
6.  
   
7.  
   
8.  
   
9.  
   
10.  
   
11.  
   
12.  
   
13.  
   
14.  
   
15.  
   
16.  
   
17.  
   
18.  
   
19.  
   
20.  
   
21.  
   
22.  
   
23.