HAVO WA, 1996 - II

 

OPGAVE 1. Controle van lotto.
       
Het Nederlandse meetinstituut te Delft controleert of de lotto een eerlijk gokspel is. Men vraagt zich daarbij af of ieder lottoballetje eenzelfde kans heeft om getrokken te worden. Hiervoor wordt de trekkingsmachine getest. Bij die test worden slechts vijf balletjes gebruikt en laat men de machine 5000 keer één balletje uit deze vijf balletjes trekken. Na iedere trekking wordt het getrokken balletje weer teruggelegd. na afloop van de 5000 trekkingen wordt geteld hoe vaak ieder van de vijf balletjes getrokken is. Deze aantallen heten de uitkomsten.
Bij een goede trekkingsmachine zal elk balletje naar verwachting 1000 keer getrokken worden. Natuurlijk zal dat meestal niet precies gebeuren. Een balletje kan bijvoorbeeld 980 keer of 1023 keer getrokken worden. Er zal sprake zijn van een zekere spreiding. In dergelijke situaties is de uitkomst van ieder balletje bij een goede trekkingsmachine vrijwel normaal verdeeld.
Neem daarom bij vraag 1  en 2 aan dat bij een goede trekkingsmachine de uitkomst van ieder balletje normaal verdeeld is met een gemiddelde van 1000 en een standaardafwijking van 28,3.
       
5p. 1. Bereken de kans dat bij het testen van een goede trekkingsmachine een bepaald balletje 950 keer of minder getrokken wordt.
       
6p. 2. Bereken de kans dat bij een goede trekkingsmachine de uitkomst van een bepaald balletje verder dan 3 keer de standaardafwijking van 1000 afligt.
       
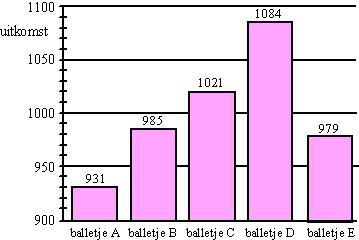
Volgens de Wet op de Kansspelen is een uitkomst die niet verder dan drie keer de standaardafwijking (hier dus 28,3) van 1000 afligt, aanvaardbaar. Ligt minstens één van de uitkomsten verder dan drie keer de standaardafwijking van 1000 af, dan zal de trekkingsmachine volgens deze Wet afgekeurd worden.

Veronderstel dat de test  van een trekkingsmachine de uitkomsten heeft opgeleverd die in onderstaande figuur staan. Voor het gemak zijn de 5 balletjes van de namen A, B, C, D en E voorzien. Bij iedere staaf staat de uitkomst van het bijbehorende balletje vermeld.
       

       
5p. 3. Moet de trekkingsmachine volgens de Wet op de Kansspelen afgekeurd worden? Licht je antwoord toe.
       
OPGAVE 2. McDonald's.
         
De fastfoodketen McDonald's heeft in verschillende landen heel wat vestigingen. Alleen al in de Verenigde Staten (VS) waar 250 miljoen mensen wonen, zijn er 9500 vestigingen. Nederland heeft 15 miljoen inwoners.

Neem eerst aan dat de verhouding van het aantal vestigingen en het aantal inwoners in Nederland even groot is als in de VS.
         
4p. 4. Hoeveel vestigingen zouden er dan in Nederland zijn? Licht je antwoord toe.
         
J. Cantapulo heeft de leiding over de internationale afdeling van McDonald's. Voor het bepalen van het gewenste aantal vestigingen, MX in een bepaald land X gaat hij uit van de volgende formule:
         
         
Het gemiddeld inkomen in een land vindt men door het totale inkomen, omgerekend in dollars, te delen door het aantal inwoners van dat land.

Het totale inkomen van Nederland is 253 miljard dollar. We schrijven dit als TINED = 253 miljard.
Voor de VS geldt  TIVS = 4950 miljard
         
5p. 5. Bereken hoe groot het gewenste aantal vestigingen in Nederland is volgens de formule van Cantapulo.
         
We gaan uit van de gegevens over de VS, te weten 9500 McDonald's vestigingen, TIVS = 4950 miljard en een bevolking van 250 miljoen mensen. De formule van Cantapulo kan vereenvoudigd worden zodat MX wordt uitgedrukt in TIX.
         
4p. 6. Stel deze formule op.
         
OPGAVE 3. Consequent.
         
Er wordt een drietal vragen aan dezelfde persoon gesteld:
Wat heeft u liever:  appels of peren?  antwoord: appels.
Wat heeft u liever:  peren of bananen?  antwoord:  peren
Wat heeft u liever:  appels of bananen? antwoord:  bananen.
Dat laatste antwoord lijkt heel onlogisch, je zou immers het woord 'appels' hebben verwacht. Toch komen zulke situaties vaak voor. Mogelijk heeft de persoon bij de eerste twee vragen gedacht aan zaken als kleur of vorm, en bij de derde vraag aan smaak.
Ook in de sport komen dergelijke situaties herhaaldelijk voor.
Bijvoorbeeld:  team A wint van team P, team P wint van team S en team S wint van team A. Zo'n drietal of tripel APS noemen we een inconsequent tripel. Een dergelijk drietal kunnen we in en gerichte graaf weergeven. Zie de onderstaande figuur.
Hierbij betekent  A → P  dat A van P wint. De pijl wijst dus van winnaar naar verliezer.
         

         
In de figuur hieronder is de gerichte graaf van een consequent tripel getekend. Team P is het sterkst en wint van Q en van R. Team Q is het zwakst en verliest van beide andere teams.
         

         
In het vervolg van deze opgave zijn er steeds vijf teams: A, B, C, D en E. In een competitie speelt elk team één keer tegen elk ander team. Neem aan dat de teams gerangschikt kunnen worden van sterk naar zwak: C → A → B → E → D.

We bekijken eerst een voorbeeld waarin alleen consequente tripels voorkomen. Iedere wedstrijd wordt gewonnen door het hoger geplaatste team. Kijken we bijvoorbeeld naar het tripel AED dan zal A van E winnen, E van D en ook A van D. Zo ontstaat het consequente tripel AED.
Ook ieder ander drietal teams vormt steeds een consequent tripel. Bij deze situatie horen een gerichte graaf en een verbindingsmatrix V.
         
6p. 7. Teken hieronder deze graaf en vul verbindingsmatrix V verder in.
         

         
Vaak echter zullen er in dergelijke competities ook inconsequente tripels te vinden zijn. Een voorbeeld daarvan is weergegeven in de graaf hieronder met de bijbehorende matrix W. Hier zien we bijvoorbeeld dat ABE een consequent tripel is en ECD een inconsequent tripel is.
         

         
6p. 8. Schrijf alle bij deze graaf horende tripels op en vermeld steeds of het om een consequent of een inconsequent tripel gaat.
         
Matrix V(van vraag 7) en matrix W(van vraag 8) en de bijbehorende grafen verschillen. De graaf van V is 'consequenter' dan de graaf die bij W hoort. De mate van consequentie van een graaf wordt uitgedrukt in de consequentiecoëfficiënt K. Deze is als volgt te berekenen:
Dit maximale aantal inconsequente tripels is natuurlijk afhankelijk van het aantal punten van de graaf.
Voor grafen met een oneven aantal punten (n) is het maximale aantal inconsequente tripels te berekenen met de volgende formule:
         
4p. 9. Hoe groot is K voor de graaf van matrix W? Licht je antwoord toe.
         
K kan ook berekend worden met behulp van de formule:
In deze formule is de maximale standaardafwijking de standaardafwijking van de kolomtotalen van matrix V uit vraag 7. Neem aan dat de maximale standaardafwijking gelijk is aan 1,41.
In deze formule is de gerealiseerde standaardafwijking de standaardafwijking van de kolomtotalen van de bijbehorende matrix. Een kolomtotaal wordt gevonden door de getallen in een kolom bij elkaar op te tellen. Bij matrix W hierboven gaat het dus om de standaardafwijking van de getallen 3, 2, 3, 1 en 1.
         
4p. 10. Bereken met deze formule K voor matrix W
         

 

OPGAVE 4.  Woestijnhagedis.
         
De woestijnhagedis (dipsosaurus dorsalis) leeft in de woestijnen van Californië (V.S.). In deze woestijnen zijn er dagelijks grote temperatuurschommelingen. In de zomer kan de temperatuur op een dag variëren van ongeveer 20ºC tot ongeveer 65ºC. In de winter kan het er zelfs vriezen. Omdat de hagedis een koelbloedig dier is, is zijn gedragspatroon erg afhankelijk van de temperatuur.
In de figuur hieronder zie je het temperatuurverloop voor een zomerdag (eind juli/begin augustus) in de Californische woestijn. Deze figuur is typerend voor alle dagen in de periode eind juli/begin augustus.
Alleen als de temperatuur tussen de 38ºC en 43ºC ligt, is de hagedis voortdurend buiten zijn hol actief met het zoeken naar voedsel.
         

         
4p. 11. Hoeveel uur per dag is de hagedis in de periode eind juli/begin augustus voortdurend buiten zijn hol actief? Licht je antwoord toe. Gebruik daarbij de figuur.
         
In de figuur is te zien dat de temperatuur tussen 6 uur en 11 uur vrij snel stijgt.
     
4p. 12. Bereken voor deze periode de gemiddelde temperatuurstijging per uur.
         
Gedurende de tijd dat de hagedis niet actief is met het zoeken naar voedsel, bevindt hij zich voornamelijk in zijn hol. In de figuur hier onder zie je een toename-/afnamediagram van de temperatuur in het hol. Ook deze figuur is typerend voor alle dagen in de periode eind juli/begin augustus. Omdat het niet zo eenvoudig was deze temperatuurmetingen te verrichten kun je hierin slechts aflezen hoeveel de temperatuur per 2 uur is gestegen of gedaald. Zo kun je bijvoorbeeld aflezen dat de temperatuur tussen 0 en 2 uur met 1,5 graden is gedaald.
         

         
Er zijn twee belangrijke verschillen tussen het temperatuurverloop buiten het hol (figuur boven vraag 11) en in het hol (figuur hierboven) Het ene heeft betrekking op de temperatuurschommeling, het andere op het tijdstip waarop de maximale temperatuur optreedt.
         
4p. 13. Beschrijf deze twee verschillen.
         
Zoals al vermeld is de woestijnhagedis buiten zijn hol als de temperatuur tussen 38 ºC en 43 ºC is. Hij heeft dan geen beschutting nodig. Als de temperatuur tussen de 43 ºC en 50 ºC is, dan moet hij af en toe beschutting zoeken tegen de zon. Bij alle andere temperaturen bevindt hij zich voortdurend in zijn hol. Er zijn dus drie fasen in het leefritme van de hagedis:
• geen beschutting nodig
• af en toe beschutting nodig
• voortdurend in zijn hol.
In de figuur linksonder kunnen we voor iedere dag van het jaar en voor ieder tijdstip op die dag de fase terugvinden waarin het leefritme van de hagedis zich bevindt.
Bovendien is er in die figuur een horizontaal strookje rond eind juli/begin augustus aangegeven. Dit strookje zien we in de figuur rechtsonder terug. In die figuur zie je hetzelfde temperatuurverloop als in de figuur boven opgave 11.
         

         
In de linkerfiguur is te zien dat de hagedis niet iedere dag even lang in de fase voortdurend in zijn hol zit. Er is één dag waarop hij de minste tijd in deze fase doorbrengt. Op die dag is de totale tijd van de andere twee fasen dus zo groot mogelijk.
         
5p. 14. In welke maand valt deze dag? Licht je antwoord toe.
         
In de linkerfiguur zie je bij half maart een horizontale stippellijn staan.
         
5p. 15. Teken met behulp van de gegevens van de linkerfiguur een grafiek van een mogelijk temperatuurverloop op 15 maart in onderstaande figuur.
         
 

         

 

OPGAVE 5.  Wie leest.
         
Voor adverteerders in een tijdschrift is het van belang te weten hoeveel mensen men met dat tijschrift bereikt. Daarom onderzoekt men voortdurend hoeveel mensen welke bladen lezen en hoe vaak. Met deze gegevens stelt men voor ieder tijdschrift een eigen leeskans op.
In deze opgave beperken we ons tot een tijdschrift met een leeskans van 0,3. Dit betekent dat iedereen, onafhankelijk van een ander, dezelfde kans van 0,3 heeft om een bepaald nummer van dat tijdschrift te lezen. Voor alle duidelijkheid: dat geldt dus steeds voor ieder nummer van dat tijdschrift. Uitgaande van deze leeskans 0,3 heeft men de volgende figuur gemaakt. In deze figuur heeft men voor alle mogelijke situaties de bijbehorende kans met een staaf (of staafje) weergegeven.
         

         
In bovenstaande figuur is te zien dat bij 5 verschenen nummers van het tijdschrift voor iedereen de kans op 0 gelezen nummers ongeveer gelijk is aan 0,17.
         
4p. 16. Laat met een berekening zien dat dit getal 0,17 correct is.
         
Sommige staven zijn in bovenstaande figuur niet of nauwelijks te zien omdat ze achter andere staven verborgen zitten. De staaf die hoort bij 2 verschenen nummers en 2 gelezen nummers is helemaal onzichtbaar.
Bij 2 verschenen nummers zijn er drie staven.
         
6p. 17. Bereken de drie kansen die bij deze staven horen.
         
Er zijn, zoals reeds vermeld, in bovenstaande figuur meer staven aanwezig dan er zichtbaar zijn.
         
5p. 18. Bereken het totaal aantal staven dat in de figuur aanwezig moet zijn.
         
Hoe vaker een tijdschrift verschijnt, hoe groter de trefkans T is dat een bepaald persoon één of meer nummers van het tijdschrift gelezen heeft. Uitgaande van de leeskans 0,3 geeft de formule  T  =  1 - (0,7)n  het verband tussen T en het aantal verschenen nummers n.
         
4p. 19. Hoeveel nummers van het tijdschrift moeten volgens deze formule minstens verschijnen opdat de trefkans groter is dan 0,999?  Licht je antwoord toe.
         

 

 

UITWERKING
   
1.  
   
2.  
   
3.  
   
4.  
   
5.  
   
6.  
   
7.  
   
8.  
   
9.  
   
10.  
   
11.  
   
12.  
   
13.  
   
14.  
   
15.  
   
16.  
   
17.  
   
18.  
   
19.  
   
20.  
   
21.  
   
22.  
   
23.