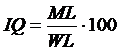HAVO WA, 1992 - II

 

OPGAVE 1.  IQ.
       
Alfred Binet ontwierp aan het begin van deze eeuw tests om de intelligentie  van kinderen vast te leggen in een getal, het intelligentiequotiënt (IQ). Later zijn deze tests door anderen uitgebreid en verbeterd.
Het IQ wordt berekend met de formule:

       
Het IQ wordt afgerond op een geheel getal. WL is de werkelijke leeftijd en ML de mentale leeftijd.
Om je mentale leeftijd ML te berekenen begin je met een test die hoort bij je eigen leeftijd. Als je die goed maakt, krijg je een serie steeds hogere tests voorgezet, net zo lang tot je een test niet meer haalt. Je mentale leeftijd is dan je werkelijke leeftijd vermeerderd met telkens 2 maanden voor elke goed gemaakte hogere test.

Een voorbeeld:  een jongen van 10 jaar en 4 maanden (werkelijke leeftijd dus WL = 10 + 4/12) maakt de test van zijn eigen leeftijd goed en nog 8 hogere tests. Voor het berekenen van zijn mentale leeftijd wordt zijn leeftijd dus met 8 · 2 = 16 maanden verhoogd en geldt dus voor hem  ML = 10 + 4/12 + 16/12 = 11 + 8/12.  Zijn IQ is dan 113.

       
(en dan afgerond op een geheel getal)

Als je de test voor je eigen leeftijd niet goed maakt, krijg je steeds lagere tests voorgelegd, net zo lang tot je er een goed maakt. Voor elke lagere test die je niet goed maakt gaat er dan 2 maanden van je mentale leeftijd af.

Een meisje van precies 12 jaar blijkt, behalve de test van haar eigen leeftijd, ook nog 21 hogere tests goed te maken.
       
3p. 1. Bereken haar IQ.
       
Het is mogelijk dat twee kinderen, behalve de test voor hun eigen leeftijd, ook nog precies 10 hogere test goed maken, maar een verschillend IQ hebben.
       
5p. 2. Geef hiervan een rekenvoorbeeld.
       
De verdeling van de IQ's van de kinderen in ons land vertoont grote overeenkomst met de normale verdeling. Neem aan dat de IQ's normaal verdeeld zijn met een gemiddelde van 100. Van 47% van de jeugd blijkt het IQ te liggen tussen 90 en 110.
       
6p. 3. Toon aan dat hieruit volgt dat de standaardafwijking bij benadering 16 is.
       
Van alle leerlingen van een bepaalde school wordt het IQ bepaald. Het resultaat is in de volgende boxplot verwerkt.
       

       
Men wil de IQ's van deze groep leerlingen vergelijken met die van de jeugd in ons land. Men kijkt daartoe naar de 'middengroep' van de kinderen van die school en de 'middengroep' van de kinderen van ons land.
Met de 'middengroep' bedoelen we de kinderen die niet horen bij de 25% kinderen met de hoogste IQ's en ook niet bij de 25% met de laagste IQ's.
       
6p. 4. Geef zowel voor die school als voor het land aan tussen welke grenzen de IQ's van de 'middengroep' liggen.
       
OPGAVE 2.  Kans op een gasexplosie.
         

         
Een schip, geladen met vloeibaar petroleumgas (LPG) ligt in de haven aan de steiger. Zo'n gastanker ligt daar meestal enige tijd voordat de lading gelost wordt. Daarna duurt het vaak nog een tijdje voordat het schip de haven weer verlaat. Men vraagt zich af hoe groot de kans is dat er in die periode een ongeluk gebeurt waarbij gas vrijkomt uit deze gastanker (met een ramp als gevolg).
Bij dit soort vragen zal men meestal proberen uit te zoeken hoe vaak zo'n ramp in het verleden heeft plaatsgevonden en op grond van die gegevens de kans op een ongeluk berekenen. In dit geval is niet bekend of er ooit zo'n ongeluk is gebeurd. Men zal dan op een andere manier de kans moeten 'berekenen'.
Met behulp van de vraag 'Wat moet er allemaal misgaan opdat de gastanker aan de steiger gas verliest?' probeert men een model op te stellen. In dat model gaat het uitsluitend om ongelukken als gevolg van een aanvaring door een ander schip.
In de volgende figuur zie je hoe zo'n model er uit zou kunnen zien.
         

         
De kansen die bij de verschillende stappen staan, gelden per periode dat een tanker aan de steiger ligt. Deze kansen zijn niet realistisch, maar bedacht. In werkelijkheid gaat het bij dit soort situaties vrijwel altijd om heel kleine kansen op ongelukken. Ga in deze opgave steeds uit van de gegevens van deze figuur.
         
3p. 8. Laat zien dat de kans op het vrijkomen van gas uit de gastanker die aan de steiger ligt bijna 2% is.
         
Per jaar verwerkt de haven 20 gastankers.
         
6p. 6. Bereken de kans op minstens 1 ongeluk per jaar in de haven door het vrijkomen van gas uit een gastanker.
         
Een ander schip raakt de geladen gastanker aan de steiger.
         
6p. 7. Bereken de kans dat er geen gas vrijkomt.
         
OPGAVE 3.  Autoverkeer.
         
Een dorp wordt door een rivier en een spoorlijn in drie wijken verdeeld, Noord, Midden en Zuid (N, M en Z). Er zijn in het dorp twee spoorovergangen (A en B) en twee bruggen (C en D) Zie de volgende figuur.
         

         
Het toenemend autoverkeer levert problemen op in het centrum van het dorp. Te veel auto's maken gebruik van spoorwegovergang B en brug C.
Om maatregelen te kunnen nemen moet men meer inzicht hebben in de verschillende verkeersstromen in het dorp. Hoeveel auto's komen waar vandaan en gaan waar naar toe? Op een willekeurige werkdag in 1989 heeft men tijdens de avondspits een kentekenonderzoek gedaan. Op een aantal plaatsen in het dorp en aan de rand van het dorp (1 t/m 5) werden de kentekens van de passerende auto's en het tijdstip genoteerd. Op grond van deze registraties heeft men achteraf de autoritten zo goed mogelijk gereconstrueerd. Ondanks het feit dat het onmogelijk is om elke autorit precies te reconstrueren, levert zo'n onderzoek een vrij betrouwbaar beeld op. Het resultaat staat in de volgende tabel.
         
 

NAAR
V
A
N		   Z M N 1 2 3 4 5 Totaal
Z
M
N		 333
140
111		 155
109
112		 107
114
176		 216
86
62		 44
59
106		 25
20
31		 50
32
43		 41
27
25		 971
587
666
1
2
3
4
5		 280
42
26
37
48		 96
101
22
25
32		 98
132
36
38
28		 33
17
11
13
19		 17
8
26
56
24		 7
17
1
17
3		 18
116
22
2
5		 37
7
1
4
1		 586
440
145
192
160
Totaal 1017 652 729 457 340 121 288 143 3747
         
Je leest bijvoorbeeld in deze tabel af dat 98 autoritten aan de rand van het dorp bij 1 begonnen en eindigde in Noord (N)

In het onderzoeksrapport staat dat 2/3 deel van alle autoritten interlokaal verkeer betrof (interlokaal verkeer is verkeer dat van buiten het dorp komt en/of dat een bestemming heeft buiten het dorp).
         
7p. 8. Onderzoek of dat klopt met de gegevens in de tabel.
         
Neem aan dat brug D uitsluitend gebruikt wordt voor de autoritten van 2 naar 3, N of 4 en omgekeerd.
         
3p. 9. Bereken het aantal autoritten over brug D.
         
Men kan het dorp aan drie kanten binnenrijden en verlaten, namelijk aan de westkant, de oostkant en de zuidkant.
         
6p. 10. Bereken aan welke kant van het dorp de autostroom het grootst is.
         
Na het onderzoek zijn voor de jaren 1993 en 2000 prognoses gemaakt. In plaats van de 3747 autoritten van 1989 verwacht men een groei tot 4104 autoritten in 1993 en 4812 in het jaar 2000.
         
5p. 11. Onderzoek of deze prognoses met een vast jaarlijks groeipercentage berekend kunnen zijn.
         

 

OPGAVE 4.  Metrokaartjes.
         

Als je in Budapest met de metro wilt reizen, moet je eerst een kaartje kopen. Zo'n kaartje is voorzien van negen vakjes met daarin de cijfers 1 tot en met 9 (zie figuur). Zodra je bent ingestapt moet je je kaartje in een ponsapparaatje steken (volgens de pijlrichting en met de bedrukte zijde boven). Eén of meer (maximaal 9) cijfers worden dan in één keer weggeponst. Daarmee is aan het kaartje te zien in welke trein je reis is begonnen.
Hiernaast zie je een afbeelding van een gebruikt kaartje, waarbij de vakjes 1, 6 en 9 zijn voorzien van een gaatje.

         
4p. 12. Bereken op hoeveel verschillende manieren er in een kaartje 3 gaatjes kunnen worden geponst.
         
In een kaartje worden 2 gaatjes geponst die niet in dezelfde rij of kolom zitten.
         
6p. 13. Hoeveel verschillende mogelijkheden zijn er? Licht je antwoord toe.
         
Het aantal cijfers dat wordt weggeponst mag variëren van 1 tot en met 9. Op een dag rijden op het metronet 400 treinen.
         
5p. 14. Is het mogelijk dat in elke trein op een verschillende wijze gaatjes in een kaartje worden geponst? Licht je antwoord toe.
         

 

OPGAVE 5.  Personenvervoer.
         
Onderstaande tabel gaat over het personenvervoer in Nederland, uitgesplitst in eigen vervoer en openbaar vervoer.
         
jaar eigen vervoer openbaar vervoer totaal
1970
1975
1977
1978
1982
1983
1984
1987		 83,2
96,0
102,3
105,2
115,8
118,6
122,8
129,9		 13,4
13,8
13,7
13,7
15,5
15,1
15,0
15,5		 96,6
109,8
116,0
118,9
131,3
133,7
137,8
145,4
         
Het aantal reizigerskilometers (in miljarden) met eigen vervoer (Ke) is in de periode 1970-1987 bij benadering toegenomen volgens een lineair verband.
Neem aan dat dit lineaire verband zich in de nabije toekomst voortzet.
         
7p. 15. Geef met behulp van een grafiek een schatting voor Ke in het jaar 2000.
         
Gezien de beperkte capaciteit van het Nederlandse wegennet en de toenemende belasting van het milieu is het onwaarschijnlijk dat het aantal reizigerskilometers met eigen vervoer onbeperkt zal blijven groeien.
Er is een formule opgesteld die bij benadering een mogelijke ontwikkeling van Ke in de toekomst beter beschrijft, namelijk:
         

         
t is de tijd in jaren, t = 0 komt overeen met 1980.
         
2p. 16. Bereken de waarde van Ke in het jaar 2000 volgens deze formule.
         
4p. 17. Beredeneer aan de hand van deze formule dat Ke op den duur nauwelijks meer zal veranderen.
         
Het aantal reizigerskilometers (in miljarden) met openbaar vervoer (Ko) is een percentage (p) van het totaal aantal reizigerskilometers in Nederland. In 1970 was dit 13,9%. In de periode 1970 - 1987 is dit percentage gedaald van 13,9 naar 10,7.
         
3p. 18. Ga na of er in de tussenliggende jaren voortdurend sprake was van een daling van dit percentage.
         
3p. 19. Stel een formule op die p uitdrukt in Ko en Ke.
         

 

 

 

UITWERKING
   
1.  
   
2.  
   
3.  
   
4.  
   
5.  
   
6.  
   
7.  
   
8.  
   
9.  
   
10.  
   
11.  
   
12.  
   
13.  
   
14.  
   
15.  
   
16.  
   
17.  
   
18.  
   
19.  
   
20.  
   
21.  
   
22.  
   
23.