HAVO WA, 1990 - I

 

OPGAVE 1.
       

       
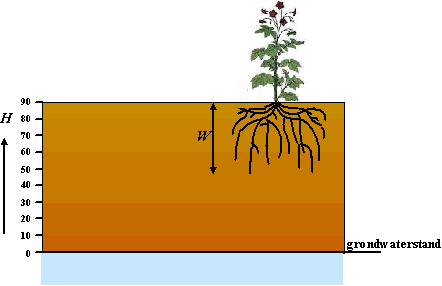
In een natuurgebied staat het grondwater op een diepte van 90 cm (zie de figuur)
Op een hoogte van 10 cm boven de grondwaterstand is het vochtgehalte van de grond ongeveer 32%. Hoe groter de hoogte boven de grondwaterstand hoe kleiner het vochtgehalte van de grond wordt. Zo is op een hoogte van 80 cm boven de grondwaterstand het vochtgehalte afgenomen tot 4%.
Het verband tussen de hoogte boven de grondwaterstand en het vochtgehalte wordt weergegeven door de formule:
 

H • p = 320
       
Hierin is H de hoogte boven de grondwaterstand, uitgedrukt in cm en p het vochtgehalte, uitgedrukt in procenten.
De formule is bruikbaar voor 10 ≤ H ≤ 80.
       
1. Teken in de figuur hiernaast een grafiek van het verband tussen H en p.

     
  Men wil een beplanting aanbrengen waarvan de wortels op hun maximale diepte een vochtgehalte tussen de 5% en 10% nodig hebben.
     
2. Bereken welke hoogten boven de grondwaterstand in aanmerking komen.
     
  De maximale worteldiepte (in cm) van een gewas in een natuurgebied noemen we W (zie de figuur bovenaan)
       
3. Geef een formule waardoor p wordt uitgedrukt in W
       
De grondwaterstand in het natuurgebied wordt 30 cm onhoog gebracht. Het verband tussen de hoogte en het vochtgehalte blijft hetzelfde als in de oude situatie.
       
4. Bereken het nieuwe vochtgehalte van de grond op een diepte van 40 cm.
       
OPGAVE 2.
         
Verkeersdrempels zijn bedoeld om de snelheid van automobilisten te beïnvloeden.
Afhankelijk van de gewenste snelheid in een straat worden de drempels steiler of minder steil gemaakt. In de volgende figuur staan twee voorbeelden.
         

         
De drempels met V85 = 50 zijn zo ontworpen dat 85% van de automobilisten de drempel passeert met een snelheid van minder dan 50 km/uur.

In de praktijk blijkt dat de passeersnelheid bij een drempel normaal verdeeld is.
Bij de drempels met V85 = 50 werd een gemiddelde passeersnelheid van 43,1 km/uur gevonden, met en standaardafwijking van 6,6 km/uur.
         
5. Laat zien dat bij deze verdeling inderdaad 85% van de automobilisten niet harder dan 50 km/uur rijdt.
         
Voor een nieuwe praktijktest zal de passeersnelheid van 1200 automobilisten worden gemeten bij een drempel met V85 = 50
         
6. Bij hoeveel van deze 1200 metingen kan, op grond van de eerdere ervaringen, een snelheid van meer dan 55 km/uur worden verwacht?
         
In een kinderrijke buurt worden verkeersdrempels met V85 = 20 aangebracht. Dat betekent dus dat 85% van de automobilisten de drempel passeert met een snelheid van minder dan 20 km/uur. De passeersnelheid is ook nu normaal verdeeld, maar met een kleinere spreiding: de standaardafwijking is 2,1 km/uur.
         
7. Bereken de gemiddelde passeersnelheid, in km/uur en op 1 decimaal nauwkeurig bij dit type drempels.
         
OPGAVE 3.
         
Hiernaast staat een fragment uit een artikel over ontwapening in de Volkskrant van 9 december 1989.
Dwars tegen de verkiezingsleuzen in kondigde de Amerikaanse minister van defensie, Richard Cheney, aan dat hij het komende begrotingsjaar op defensie 15 miljard dollar wil bezuinigen.
Dat is 5 procent van de defensiebegroting van 1989
....
Het Amerikaans weekblad Business Week liet de economische gevolgen van deze diep ingrijpende bezuinigingen  doorrekenen, uitgaande van een bezuiniging van 5 procent per jaar op defensie.
     
Het uit de tekst hiernaast niet duidelijk wat Business Week bedoelt met een bezuiniging van 5% per jaar op defensie.
De volgende twee opvattingen zijn mogelijk:
(a) de defensie begroting wordt, te beginnen met 1990, elk jaar verminderd met 5% van de begroting van 1989.
(b) de defensiebegroting wordt elk jaar verminderd met 5% van de begroting van het voorafgaande jaar.
Dat maakt wel degelijk verschil.
         
8. Zoek voor beide opvattingen uit hoeveel jaar het duurt voor de defensiebegroting gehalveerd is ten opzichte van de begroting van 1989.
         
9. Geef voor beide opvattingen een formule voor de defensiebegroting (in miljarden dollar) afhankelijk van het aantal jaren.
         
OPGAVE 4.
         
Oudheidkundigen proberen informatie te krijgen over de voedselsituatie van vroegere bewoners van een nederzetting. Uit botjes in afvalputten blijkt welke dieren men vroeger at en soms ook hoeveel. Niet is bekend hoeveel voedsel een rund uit die tijd opleverde, maar daarover zou de grootte van het dier informatie kunnen geven.
Als maat voor de grootte neemt men de schofthoogte (zie figuur). Meestal ontbreken er botten die nodig zijn om de schofthoogte te bepalen. Vaak treft men wel een middenvoetsbeentje (metacarpus) aan.
         

         
Men heeft voor twee runderrassen, A en B, kunnen vaststellen dat er tussen de metacarpus en de schofthoogte een verband bestaat. Dat verband verschilt per ras.
Onderstaande grafiek geeft het verband tussen de schofthoogte (s) en de lengte van de metacarpus (m) voor ras A.
         

         
10. Stel een formule op die bij deze grafiek past.
         
Voor ras B geldt de formule  s = 5m + 16  (5 ≤ m ≤ 25)
         
11. Teken in de figuur hierboven ook de grafiek van ras B.
         
12. Bereken in millimeters nauwkeurig bij welke waarde van m de schofthoogten van beide rassen gelijk zijn.
         
In theorie zou bij opgegeven waarden van m en s van een dier vastgesteld kunnen worden of het een dier van ras A of van ras B betreft, met uitzondering van de situatie zoals bedoel in vraag 12.
In werkelijkheid is het verband tussen de lengte van de metacarpus en de schofthoogte niet zo precies als de formules aangeven.
We nemen aan dat bij elke lengte van de metacarpus de schofthoogte kan variëren van 2 cm onder de aangegeven waarde tot 2 cm erboven.
         
13. Bepaal met behulp van de grafieken hierboven bij welke lengten van de metacarpus er problemen kunnen optreden bij het vaststellen van het ras.
         
Uit de schofthoogte kan bij benadering het levend gewicht van een rund worden afgeleid. Er blijkt een verband te bestaan dat nagenoeg lineair is. Gegevens over dit verband staan in de volgende tabel.
         
schofthoogte
(cm)		 levend gewicht ras A
(kg)		 levend gewicht ras B
(kg)
110
120		 400
470		 380
435
         
De lengte van een gevonden metacarpus is 21 cm. Het botje kan van een rund van ras A of van ras B zijn.
         
14. Bereken voor beide mogelijkheden het levend gewicht.
         

 

OPGAVE 5.
         
Een planoloog wil graag weten op grond van welke eigenschappen de bewoners de straten van hun wijk beoordelen. Als onderdeel van zijn onderzoek legt hij een aantal proefpersonen groepjes van drie straten voor. Hij vraagt hen bij elk groepje aan te wijzen welke twee van de drie straten het meest op elkaar lijken.
Het onderzoek heeft betrekking op 10 straten, voor het gemak A, B, C, D, E, F, G, H, K, L genoemd. Hieruit worden alle mogelijke groepjes van drie gevormd en elk groepje wordt in alfabetische volgorde op een kaartje geschreven. In de volgende figuur zie je drie voorbeelden.
         

         
15. Hoeveel kaartjes zijn er nodig?
         
16. Op hoeveel kaartjes komt straat A voor?
         
17. Op hoeveel kaartjes komen de straten A en B samen voor?
         
Een proefpersoon is bereid om bij alle kaartjes zijn keuze te maken.
         
18. Onderzoek of het mogelijk is dat hij 7 keer voor de combinatie AB, 7 keer voor de combinatie AC en 7 keer voor de combinatie AD kiest.
         
OPGAVE 6.
       
Voedseldeskundigen willen weten welke vogelsoorten in een bepaald gebied leven. Een eenvoudige manier om daar achter te komen is het maken van een ronde door dat gebied en alle waargenomen vogels te registreren.
Men spreekt van een registratie-effectiviteit van 100% wanneer alle aanwezige vogels opgemerkt worden.
In de praktijk blijkt de registratie-effectiviteit per ronde slechts 60% te zijn, de overige 40% van de totale vogelpopulatie wordt niet opgemerkt.
De Zweedse vogeldeskundige Anders Enemar stelt dat de registratie-effectiviteit door het maken van drie ronden zodanig verhoogd wordt dat men vrijwel zeker mag aannemen dat alle vogelsoorten zijn opgemerkt.
Hij neemt daarbij aan dat iedere aanwezige vogel bij elke ronde 60% kans heeft om opgemerkt te worden. 
       
19. Bereken hoeveel procent van de totale populatie naar verwachting na drie ronden nog niet zal zijn opgemerkt.
       
Na drie ronden is de vogelpopulatie verdeeld in vier categorieën:  I, II, II, IV.
  I:   niet opgemerkt.
II:  één keer opgemerkt
III: twee keer opgemerkt
IV: drie keer opgemerkt.
       
20. Welk van die vier categorieën bevat de meeste exemplaren? Licht je antwoord toe met een berekening.
       
Stel dat er bij iedere ronde ongeveer 450 vogels worden opgemerkt
       
21. Bereken hoeveel vogels er bij de derde ronde voor het eerst worden opgemerkt.
       

 

UITWERKING
   
1.  
   
2.  
   
3.  
   
4.  
   
5.  
   
6.  
   
7.  
   
8.  
   
9.  
   
10.  
   
11.  
   
12.  
   
13.  
   
14.  
   
15.  
   
16.  
   
17.  
   
18.  
   
19.  
   
20.  
   
21.  
   
22.  
   
23.