HAVO WA12, 2008 - II
Ei.

Alle eieren die je in de winkel koopt, zijn tegenwoordig voorzien van een code. Het ei op de foto heeft als code 2-NL-4017701. Dit is de IKB-code. (IKB betekent integrale ketenbeheersing.) Hiermee is te achterhalen waar het ei vandaan komt. In de volgende tabel zie je hoe de IKB-code is opgebouwd.

Houderijsysteem Land van
herkomst		 Nummer
pluimveebrdrijf		 Eventueel
stalnummer
0 = biologisch
1 = Vrije uitloop
2 = Scharrel
3 = Kooi		 NL = Nederland
BE = België
DE = Duitsland
FR = Frankrijk		 5 cijfers:
10000 t/m 99999		 2 cijfers:  00 t/m 99

Het ei op de foto is dus een scharrel-ei uit Nederland van pluimveebedrijf 40177 met stalnummer 01.
3p. 1. Bereken hoeveel verschillende IKB-codes mogelijk zijn.

Het gewicht van een ei is bij benadering normaal verdeeld met een gemiddelde van 61,0 gram. De eieren worden in gewichtsklassen ingedeeld volgens de volgende tabel.
Klasse Gewicht
S (small) minder dan 53,0 gram
M (medium) van 53,0 gram tot 63,0 gram
L (large) van 63,0 gram tot 73,0 gram
XL (extra large) vanaf 73,0 gram

De klassenbreedtes van de klassen M en L zijn even groot. Toch zitten er meer eieren in klasse M dan in klasse L.
3p. 2.

Leg zonder berekening uit waarom er in klasse M meer eieren zitten dan in klasse L.

Verder is bekend dat de standaardafwijking van het gewicht van de eieren 10,0 gram is.
3p. 3. Bereken het percentage eieren in klasse XL.

Door de indeling uit tabel 2 komt 21,2% van de eieren in de lichtste klasse S terecht. Voor deze eieren krijgen de pluimveebedrijven de laagste prijs. De Nederlandse organisatie van pluimveehouders wil daarom de klassengrens van 53,0 gram verlagen, zodat slechts 15% van de eieren in klasse S terechtkomt.
4p. 4.

Bereken met hoeveel gram deze klassengrens dan verlaagd zou moeten worden. Geef je antwoord in één decimaal.

 

Alcoholgehalte.

Het drinken van alcoholische consumpties beïnvloedt de rijvaardigheid negatief. Het is in Nederland dan ook verboden om met een alcoholgehalte van meer dan 0,05 een auto te besturen. Dit alcoholgehalte heet het bloedalcoholgehalte, afgekort BAG. Het BAG is afhankelijk van verschillende factoren:
- de hoeveelheid alcohol die je drinkt;
- je gewicht;
- of je een man of een vrouw bent;
- de tijd die verstreken is na de laatste alcoholconsumptie.
Er zijn formules opgesteld waarmee je vrij nauwkeurig kunt berekenen wat je BAG is. Voor mannen en vrouwen zijn de formules dus verschillend:

BAGman = 0,01241• h • p • m −1 − 0,017 • t
BAGvrouw = 0,01535 • h • p • m −1 − 0,016 • t

Hierin is:
h de hoeveelheid alcoholische drank in cl (centiliter)
m het lichaamsgewicht in kg
t de tijd in uren na de laatste alcoholconsumptie

Als er geen alcohol in het bloed zit, is het BAG nul. Een man van 79 kg drinkt op een avond 3 flesjes bier van elk 30 cl, met een alcoholpercentage van 5% (dus p = 5).
4p. 5.

Toon aan dat er ongeveer 4 uur en 10 minuten na de laatste alcoholconsumptie geen alcohol meer in zijn bloed zit.

Een man en een vrouw hebben tijdens een etentje samen een fles rode wijn van 75 cl leeggedronken. Die wijn bevatte 12,5% alcohol. De man van 85 kg heeft uiteindelijk 45 cl van de wijn op en de vrouw van 68 kg 30 cl. Ze dronken tegelijk hun laatste slok wijn op.
Na deze laatste slok willen ze zo snel mogelijk naar huis. Ze willen hierbij niet het verbod overtreden om een auto te besturen met een BAG van meer dan 0,05.
5p. 6. Wie mag als eerste de auto besturen? Licht je antwoord toe.
In de rest van de opgave gaan we uit van mannen die direct na de laatste alcoholconsumptie (willen) autorijden. De formule wordt dan:

BAGman = 0,01241 • h • p •m−1

Een jonge man wil weten hoeveel hij kan drinken om meteen daarna nog steeds te mogen autorijden zonder het verbod te overtreden. De man weegt 83 kg en drinkt flesjes bier met een alcoholpercentage van 5. In een flesje zit 30 cl bier.
3p. 7.

Hoeveel flesjes bier mag de man dan volgens de wettelijke norm maximaal drinken? Licht je antwoord toe.

Onderzoek wijst uit dat bij BAG = 0,09 het risico op een ongeval twee keer zo groot is als bij een BAG van 0. Dit kun je aflezen uit de grafiek in onderstaande figuur 1. Op de verticale as is de risico-index aangegeven, waarbij het risico op een ongeval bij BAG = 0 op 1 is gesteld. Bij BAG = 0,09 is de risico-index 2, dus 100% groter. Uit de grafiek blijkt dat de risico-index vanaf een BAG van 0,08 fors toeneemt en dus ook het risico op een ongeval.

Een man van 85 kg heeft zojuist 6 glaasjes jenever op met een alcoholpercentage van 40. In elk glaasje zit 3 cl jenever. Hij vraagt zich af hoe de risico-index toeneemt wanneer hij nog een glaasje neemt.
8.

Bereken met hoeveel procent de risico-index dan toeneemt. Licht je werkwijze toe.

Bij een vaste hoeveelheid drank geldt: hoe zwaarder men is, hoe lager het BAG.
Voor mannen die 75 cl wijn drinken met 12,5% alcohol geldt de formule:

               BAGman =11,634 • m−1
4p. 9. Stel de afgeleide op en toon met behulp van die afgeleide aan dat hier inderdaad geldt: hoe zwaarder, hoe lager het BAG.

 

De Antarctische pelsrob.

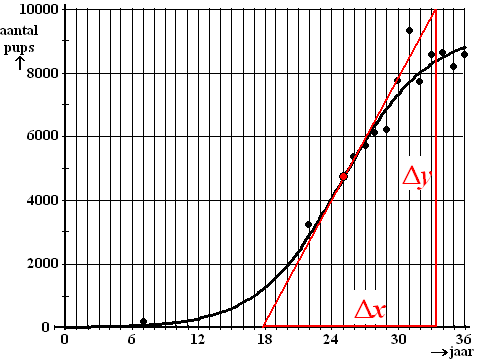
Op eilandjes in de buurt van Antarctica leven weer grote populaties van de Antarctische pelsrob. Dat is bijzonder want ze waren bijna uitgeroeid. In het begin van de 19e eeuw is er namelijk zeer veel op deze robben gejaagd vanwege hun pels.
Heel lang werd er geen enkel exemplaar gesignaleerd, maar zo’n veertig jaar geleden werd er een kleine populatie ontdekt. De natuurlijke groei van deze populatie is gevolgd. Over de aantallen van deze populatie gaat deze opgave.

Sinds 1966 is met tussenpozen het aantal pups (jonge pelsrobben) geteld. In onderstaande figuur zijn deze aantallen met bolletjes weergegeven.

De bolletjes liggen bij benadering op de grafiek waarbij de volgende formule hoort:
Hierin is N het aantal pups en t de tijd in jaren, met t = 0 op 1 januari 1966.
Op 1 januari 2002 werden er 8577 pups geteld.
De formule geeft voor 1 januari 2002 een aantal dat daar iets van afwijkt.
4p. 10.

Bereken hoeveel procent het aantal volgens de formule afwijkt van het getelde aantal.
4p. 11.

Bereken met de formule in welk jaar het aantal pups voor het eerst groter is dan 9250.

Op 1 januari 1966 werden er 12 pups geteld. Op 1 januari 1991, 25 jaar later, werden er 4650 pups geteld. Tussen die jaren was er bij benadering sprake van exponentiële groei van het aantal pups.
4p. 12.

Bereken met hoeveel procent per jaar het aantal pups in deze periode is gegroeid.

Op 1 januari 1991 werden er 4650 pups geteld. Op t = 25 is de grafiek het steilst. De hellingscoëfficiënt is daar dus het grootst.
2p. 13. Leg uit wat de hellingscoëfficiënt zegt over het aantal pups.
4p. 14.

Onderzoek hoe groot de hellingscoëfficiënt van de grafiek op t = 25 is.

 

Erupties.

Vulkanen kunnen heel lang niet-actief zijn. Dan zijn er geen erupties (uitbarstingen). Tijdens een actieve periode van een vulkaan zijn er wel erupties. Bij een eruptie komt er gesmolten steen, gas en as uit de vulkaan. Dat duurt een tijdje. Daarna is de vulkaan weer rustig, totdat de volgende eruptie begint. We bekijken in deze opgave één actieve periode van één vulkaan. De actieve periode start bij de eerste eruptie.
Wetenschappers hebben tijdens deze actieve periode gemeten:
- hoe lang iedere eruptie duurt: de eruptieduur;
-

hoe lang de vulkaan rustig is tot de volgende eruptie begint: de tussentijd tot de eerstvolgende eruptie.
Tijdens deze actieve periode was de langste tijd tussen twee erupties 108 minuten. Na de allerlaatste eruptie was de vulkaan weer lange tijd rustig. De eruptieduur is gemeten in tienden van een minuut nauwkeurig en de tussentijd in gehele minuten. De metingen zijn verwerkt in onderstaande figuur. De eruptieduur E staat langs de horizontale as, de tussentijd tot de eerstvolgende eruptie T staat langs de verticale as.

Het meest linkse punt in de figuur hoort bijvoorbeeld bij een eruptie die 0,8 minuut duurde en waarna de vulkaan 49 minuten rustig was. 
In deze actieve periode zijn er 184 erupties geweest. De eerste 183 zijn weergeven in de figuur. De allerlaatste eruptie van deze actieve periode duurde 1,7 minuut.

De allerlaatste eruptie van een actieve periode kan niet in zo’n figuur worden weergegeven.
2p. 15. Geef hiervoor de verklaring.

We bekijken alleen de gegevens uit de figuur en laten de 184e eruptie buiten beschouwing.

Je kunt de gemiddelde duur van de 183 erupties schatten met behulp van de onderstaande klassenindeling (tabel). Bij een aantal klassen zijn de frequenties al gegeven.
eruptieduur E (in minuten,
afgerond op tienden)		 0 - 0,9 1 - 1,9 2 - 2,9 3 - 3,9 4 - 4,9 5 - 5,9
frequentie 1 34     93 9
5p. 16. Bereken de gemiddelde eruptieduur met behulp van de klassenindeling.

Je kunt op een soortgelijke manier voor de 183 erupties de gemiddelde duur van de tussentijd T schatten. Het blijkt dat de tussentijd gemiddeld ongeveer 73 minuten bedraagt.
4p. 17.

Toon aan dat deze actieve periode van de vulkaan langer heeft geduurd dan een week.
In de volgende figuur is een lijn getrokken die zo goed mogelijk bij de metingen past.

Deze lijn gaat door de punten (2, 56) en (5, 90). Met behulp van deze lijn kun je bij een gegeven eruptieduur een grove schatting maken voor de tussentijd die je daarbij kunt verwachten.
4p. 18. Stel een formule op die bij deze lijn hoort.

Bierkenners vallen door de mand.

Je kent ze waarschijnlijk wel, die jongens met een uitgesproken mening over hun favoriete biermerk. Ze willen alleen dát merk; de rest is bocht. Maar wat bleek in een biertest van de Consumentenbond? Het gaat voor een belangrijk deel om het imago; bijna niemand herkent zijn favoriete merk.

Bij de biertest worden vijf flesjes bier van vijf verschillende merken naast elkaar gezet.
3p. 19.

Bereken het aantal volgordes waarin de vijf flesjes naast elkaar gezet kunnen worden.

De vijf flesjes staan geopend en zonder etiket naast elkaar. De twaalf deelnemers aan de test weten om welke vijf merken het gaat. Een ervan is hun favoriete merk, maar ook de andere merken hebben ze wel eens gedronken. Ze moeten proberen bij ieder flesje het juiste merk te noemen.
Geen van de twaalf bierkenners is in staat bij alle vijf flesjes het juiste merk te noemen. En maar liefst zeven van de twaalf deelnemers herkennen geen enkel merk. In de volgende tabel staan nog meer uitkomsten van deze test.
Aantal goed 0 1 2 3 4 5
Aantal 
bierkenners		 7 .... 1 1 .... 0
4p. 20.

Vind de twee ontbrekende getallen van deze tabel en bereken hoeveel de deelnemers er gemiddeld goed hadden

Wanneer je gokt, is de kans dat je géén van de vijf biermerken ‘herkent’ ongeveer 0,3667. Als twaalf mensen zo’n test doen en bij elk flesje gokken, kun je de kans berekenen dat iedereen alles fout raadt. Die kans is erg klein.
3p. 21. Bereken deze kans.

We kijken naar een iets eenvoudiger situatie. Er zijn nu geen vijf maar vier flesjes van vier verschillende merken: A, B, C en D. En we gaan ervan uit dat er geen biermerken worden herkend, maar dat er wordt gegokt.
Om de kans te berekenen dat geen enkel merk goed wordt geraden, is het handig om alle gokmogelijkheden systematisch in een tabel te verzamelen. In tabel 2 staat het begin van zo’n tabel. Deze tabel staat ook op de uitwerkbijlage. De vier flesjes staan in de volgorde A, B, C, D naast elkaar. Zie de volgende tabel.

In gokmogelijkheid 1 worden alle vier biermerken goed gegokt. Je hebt er dus 4 goed.
Bij de gokmogelijkheden 2 en 3 zijn twee biermerken goed en bij gokmogelijkheid 4 is slechts één merk goed geraden.
5p. 22. Vul de tabel op hiernaast verder in en laat met behulp van die tabel zien dat bij gokken de kans op 0 goed gelijk is aan 0,375.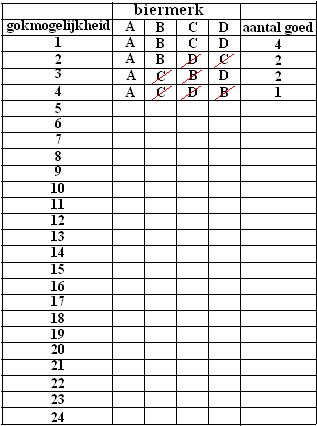
Bij het gokken van vier biermerken kun je de verwachtingswaarde van het aantal merken dat je goed raadt berekenen. Voordat je deze verwachtingswaarde kunt berekenen, moet je eerst de overige kansen in de kansverdeling uit de tabel hieronder berekenen.
Aantal goed geraden 0 1 2 3 4
kans 0,375        
4p. 23. Stel de volledige kansverdeling op en bereken daarmee de verwachtingswaarde van het aantal goed geraden merken.

 

UITWERKING
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
1. 1e cijfer: 4 mogelijkheden.
2 letters: 4 mogelijkheden.
5 cijfers: 10000 tm 99999 is 90000 mogelijkheden
2 cijfers:  00 tm 99 is 100 mogelijkheden
in totaal geeft dat  4 • 4 • 90000 • 100 = 144000000 mogelijkheden.
2. Het gemiddelde zit in klasse M en een klokvorm is het hoogst bij het gemiddelde, dus is daar de oppervlakte (bij gelijke breedte) ook het grootst.
3. normalcdf(73.0, 1000000, 61.0, 10.0) = 0,115 en dat is  11,5%
4. normalcdf(0, X, 61.0, 10.0) = 0,15
Y1 =  normalcdf(0, X, 61.0, 10.0) en Y2 = 0,15 en dan intersect geeft  X = 50,6
Dan moet de grens dus met 2,4 verlaagd worden. 
5. m = 79 en  h = 3 • 30 = 90  en  p = 5 en t = 41/6 uur invullen:
BAGman = 0,01241 • 90 • 5 • 79-1 - 0,017 • 41/6 = -0,0002
Er zit dus geen alcohol meer in zijn bloed.  
6. de man:
p = 12,5 en m = 85 en h = 45 geeft  BAGman = 0,01241 • 45 • 12,5 • 85-1 - 0,017t  = 0,082125 - 0,017t
Dat is 0,05 als  0,082125 - 0,017t = 0,05  ⇒  -0,017t = -0,032125  ⇒  t = 1,8897

de vrouw:
p = 12,5  en  m = 68 en h = 30 geeft  BAGvrouw = 0,01535 • 30 • 12,5 • 68-1 - 0,016t = 0,08465 - 0,016t
Dat is 0,05 als  0,08465 - 0,016t = 0,05  ⇒  -0,016t = -0,03465  ⇒  t = 2,1656

de man mag als eerste de auto besturen.
7. m = 83  en p = 5 geeft  BAGman = 0,01241 • h • 5 • 83-1 = 0,05
dus 0,00074759h = 0,05  ⇒  h = 66,88 cl
In een flesje zit 30 cl, dus dat zijn  66,88/30 = 2,23 flesjes. De man mag dus 2 flesjes drinken. 
8. m = 85,  p = 40
6 glaasjes:  h = 6 • 3 = 18 en dus BAGman = 0,01241 • 18 • 40 • 85-1 = 0,105
de grafiek geeft dan een risicoindex van ongeveer 3
7 glaasjes:  h = 7 • 3 = 21 en dus  BAGman = 0,01241 • 21 • 40 • 85-1 = 0,123
de grafiek geeft dan een risicoindex van  ongeveer 5
De risicoindex neemt dus 2 toe en dat is  2/3 • 100% = 67% toename
9. BAG' = 11,634 • -1 • m -2 = -11,634 • m-2  =  -11,634/m² 
m2 is altijd positief, dus er staat een neagtief gedeeld door een positief getal.
dat is negatief. 
De afgeleide negatief betekent dat de grafiek van BAG daalt, dus dat als m toeneemt, dat dan BAG afneemt.
10. 1 januari  2002 is  t = 36.
N = 9300/(1 + 0,76911) = 8810
Het getelde aantal was 8577 dus dat scheelt  233 pups
Dat is 233/8577 • 100% = 2,7% 
11. plot Y1 = 9300 / (1 + 0,769^(X-25)) en  Y2 = 9250.
intersect levert X = 44,9
t = 44 is 1 januari 2010 en t = 45 is 1 januari 2011, dus het zal zijn eind 2010.
12. Als de groeifactor per jaar gelijk is aan g dan geldt er  4650 = 12 • g25 
Dus g25 = 4650/12 = 387,5 en daaruit volgt  g = 387,5(1/25) = 1,27
Dat is dus per jaar 27% groei. 
13. De hellingscoëfficiënt is de toenamesnelheid, dus geeft aan hoeveel pups er per tijdseenheid bijkomen. 
14. Het is de helling van de raaklijn is de figuur hiernaast.
Die is gelijk aan Δy/Δx
 Δy = 10000
 Δx = 33,5 - 17,5 = 16

helling = 10000/16  ≈ 625

 
15. Je weet de tussentijd tot de volgende eruptie niet.
16. In klasse 2 - 2,9 vallen 31 metingen en in klasse 3 - 3,9 vallen 15 metingen
De klassenmiddens zijn  0,45 en 1,45 en 2,45 en 3,45 en 4,45 en 5,45
Dat geeft gemiddeld  (0,45 • 1 + 1,45 • 34 + 2,45 • 31 + 3,45 • 15 + 4,45 • 93 + 5,45 • 9)/183 ≈ 3,5 minuut

(misschien is de eerste klasse eigenlijk 0,05 - 0,9  immers erupties van lengte 0kleiner dan 0,05 worden afgerond naar 0 en zijn er dus niet).
in dat geval wordt het eerste klassemidden 0,475 maar het gemiddelde blijft ongeveer hetzelfde)
17. De gemiddelde tussentijd is 73 minuten en er zijn 183 tussentijden geweest (184 erupties)
De tussentijden duurden samen dus 73 • 183 = 13359 minuten
183 erupties duurden gemiddeld 3,5 minuten dus dat kostte in totaal  183 • 3,5 = 640,5 minuten
Samen is dat 13359 + 640,5 = 13999,5 minuten
een week heeft  60 • 24 • 7 = 10080 minuten
Dus de actieve periode was (ook zonder de 184e eruptie) meer dan een week.
18. lijn door (2, 56) en (5, 90) heeft vergelijking  y = ax + b
a = Δy/Δx = (90 - 56)/(5 - 2) = 111/3.
y = 111/3x + b
punt (2,56) invullen:  56 = 111/3 • 2 + b  ⇒  56 = 222/3 + b  ⇒  b = 56 - 222/3 = 331/3
de vergelijking is dus  T = 111/3 • E + 331/3.
19. 5 • 4 • 3 • 2 • 1 = 120 manieren
20. 4 flesjes goed is onmogelijk want dan heb je ook het vijfde flesje goed.
Er zijn er dus 0 met 4 goed en 3 met 1 goed geweest.
Het gemiddelde is dan  (0 • 7 + 1 • 3 + 2 • 1 + 3 • 1 + 4 • 0 + 5 • 0)/12 = 2/3
21. Als voor één persoon de kans gelijk is aan 0,3667, dan is voor 12 personen de kans dat iedereen alles fout heeft  0,366712 ≈ 0,0000059
22.
Dat is hiernaast gebeurd.

0 goed:  9 keer van de 24.
De kans is daarom 9/24 = 0,375
23.
Aantal goed geraden 0 1 2 3 4
kans 9/24 8/24 6/24 0 1/24
Afgelezen uit de tabel van vraag 22.
Verwachtingswaarde is  E = 0 • 9/24 + 1 • 8/24 + 2 • 6/24 + 3 • 0 + 4 • 1/24 = 1