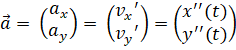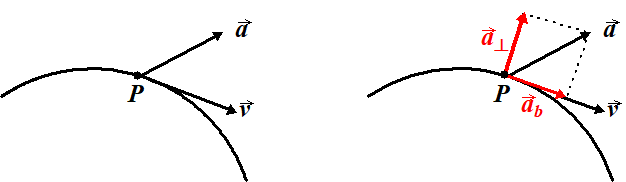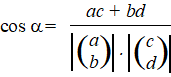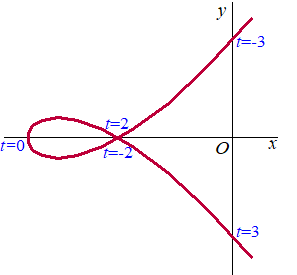versnelling vector

© h.hofstede (h.hofstede@hogeland.nl)

Versnelling.

De versnelling a zegt hoe snel de snelheid v verandert. In één dimensie is de zaak makkelijk en kun je gewoon stellen a = v' (net zoals x = s': de snelheid is hoe snel de afstand s verandert).
Bij bewegingen in een vlak heb je uiteraard weer te maken met een snelheidvector;

a_x is de versnelling in de x-richting, dus die zegt hoe snel de snelheid in de x-richting verandert, en op dezelfde manier zegt ay hoe snel v_y verandert.
Er geldt dus a_x = v_x' en a_y = v_y'
Maar die v_x en v_y waren zélf ook al de afgeleide, namelijk van x(t) en y(t)
Daarom geldt:

Daar rechts staat dus de afgeleide van de afgeleide; ofwel de tweede afgeleide.
Die versnelling is een vector dus heeft een grootte en een richting. Laten we die beiden maar weer apart onder de loep nemen;

grootte van de versnelling.

De grootte van versnelling van punt P is eigenlijk hetzelfde als de kracht die op punt P werkt. De tweede wet van Newton (natuurkunde) zegt F = m • a waarin F de kracht is en m de massa. De versnelling is dus eigenlijk de kracht per eenheid massa. (voor een massa 1 is de versnelling precies hetzelfde als de kracht).

"De versnelling (kracht) zorgt ervoor dat de snelheid verandert".

Maar de verandering van de snelheid hangt niet alleen af van de grootte van de versnelling, maar ook van de richting. Als de versnelling in tegengestelde richting als de snelheid is, zal punt P afremmen, en als de versnelling in dezelfde richting als de snelheid is zal punt P versnellen. Helaas zijn er ook allerlei tussenvarianten mogelijk, en daarom gaan we naar:

richting van de versnelling.

Bij de snelheid was alles nog simpel: de richting van de snelheid is de richting van de baan immers die kant op beweegt het punt P nou eenmaal. Bij de versnelling is dat anders, die kan best een andere richting hebben dan de snelheid.

Links zie je het geval waarin versnelling en snelheid een hoek met elkaar maken. Het is dan handig om de versnelling in twee componenten te ontbinden, zoals in de tekening rechts:

•

De component a_b is de baanversnelling.
Dat is de component van de versnelling die evenwijdig aan de snelheid is. Je kunt het zien als het deel van de versnelling dat helpt om de snelheid te vergroten.

•

De component a_⊥ is de loodrechte versnelling.
Dat is de component van de versnelling die loodrecht op de snelheid staat. Je kunt het zien als het deel van de versnelling dat de richting van de snelheid verandert (dus de baan van punt P laat ombuigen).

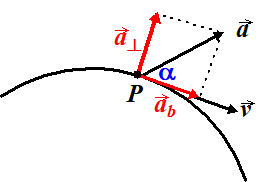
Kijk maar naar de figuur hiernaast.
Als de hoek α tussen de versnellingsvector en de snelheidsvector bekend is, kun je eenvoudig sos-cas-toa toepassen:

a_b = a • cosα
a_⊥₌a • sinα

Denk erom dat die a's hierin de groottes van de vectoren voorstellen, niet de vectoren zelf.

En die hoek α tussen twee vectoren kunnen we met een eenvoudige formule uit een vorige les berekenen. Ik citeer daaruit:

Vertaald naar onze vectoren v en a geeft dat (pijltjes zijn vectoren, gewone letters zijn groottes):

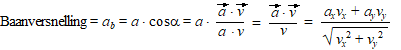Voor de loodrechte versnelling zou je cosα kunnen bepalen, dan daaruit sinα en dan a_⊥.
Maar voor alleen maar de grootte kun je net zo goed Pythagoras gebruiken: a² = a_b² + a_⊥²

Voorbeeld.

De plaatsvector OP bij de figuur hiernaast wordt gegeven door:

De versnellingsvector is dan:

en de versnellingsvector:

voor de baanversnelling geldt:

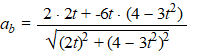Voor t = 2 geldt bijvoorbeeld

•

P = (-5, 0)

•

a_b = ^{(2 • 4 - 12 • -8)}/_{√(16
+ 64)} = ¹⁰⁴/_√80 ≈ 11,63

•

a_⊥ = √(148 - 11,63²) = √12,8 ≈ 3,58

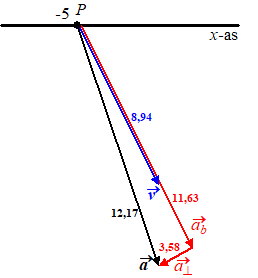
Zie de figuur hiernaast.
Merk nog op dat a_⊥ de snelheid v naar linksonder zal laten afbuigen.
Verder is a_b groter dan a_⊥ , en in de richting van v, dus de snelheid van punt P zal op t = 2 veel groter worden en een beetje naar beneden worden afgebogen.


OPGAV EN