|
|||||
| 1. | a. |
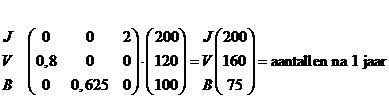 |
|||
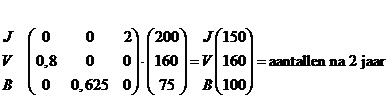 |
|||||
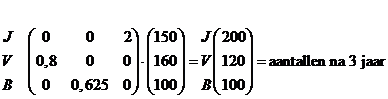 |
|||||
| b. | Na 4 jaar komt de
bevolkingshoeveelheid van na 1 jaar er weer uit! Dat betekent dat er om de drie jaar hetzelfde zal gebeuren. Deze drie bevolkingsopbouwen blijven elkaar afwisselen/opvolgen. |
||||
| c. | Stel dat de aantallen
200 - X - 100 zijn Dan zijnde aantallen over een jaar 200 - 160 - 0,625X Dus moet gelden X = 160 Dan is inderdaad 0,625X = 100 De vogelliefhebber moet dus 40 volwassen vogels toevoegen. |
||||
| 2. | a. | Omdat de bevolkingsgroepen 5 jaar breed zijn betekent elke vijf jaar dat je één keer met M moet vermenigvuldigen: | |||
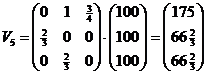 |
|||||
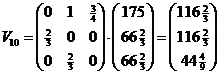 |
|||||
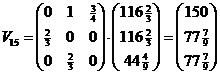 |
|||||
| b. | Stel die hoeveelheden J, V en B,
dan geldt: 1 • V + 3/4 • B = J 2/3 • J = V 2/3 • V = B Uit de tweede volgt J = 1,5V en uit de derde B = 2/3V en die kun je samen invullen in V + B + J = 400 Dat geeft 25/6V = 400 dus V = 96 Dan is B = 64 en J = 144 |
||||
| c. |
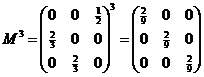 |
||||
| Dat betekent dat om de drie jaar de hoeveelheid in elke leeftijdsgroep wordt vermenigvuldigd met 2/9. Dus de totale hoeveel ook om de drie jaar. | |||||
| d. | De groeifactor van
het totale aantal is 2/9
per 3 jaar (zie vraag c) 30000 • (2/9)x = 50 geeft x = 4,25 Dat is na 4,25 • 3 = 13 jaar. |
||||
| 3. | a. | De lesliematrix is de volgende: | |||
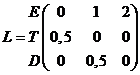 |
|||||
| Over 5 dagen moet je L5 toepassen op de bevolkingsopbouw nu: | |||||
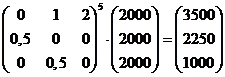 |
|||||
| b. | 1 • T + 2 • D = E 0,5 • E = T 0,5 • T = D E + T + D = 6300 De tweede geeft E = 2T en de derde geeft D = 0,5T en die kun je invullen in de vierde: 2T + T + 0,5T = 6300 dus T =1800 Dan is E = 3600 en D = 900 De opbouw is 3600 - 1800 - 900 |
||||
| 4. | De lesliematrix is de volgende (als 10 Jongen één volwassenen voortbrengen, dan brengt één Jonge gemiddelde 0,1 volwassenen voort): | ||||
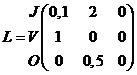 |
|||||
| Over 6 weken vermenigvuldigen met L6 : | |||||
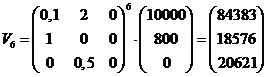 |
|||||
| Dat zijn er in totaal 123580. | |||||
| 5. | a. | Elk exemplaar heeft per periode gemiddeld 0,25 nakomelingen | |||
| b. |
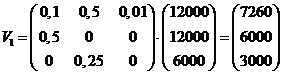 |
||||
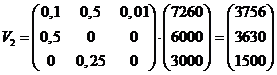 |
|||||
| 6. | a. | de 1210 exemplaren van 1-2 maanden oud zijn een periode later veranderd in de 1030 exemplaren van 2-3 maanden oud. De kans dat een exemplaar nog leeft is dus 1030/1210 = 0,85 | |||
| b. |
 |
||||
| c. |
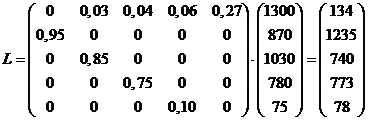 |
||||
| De laatste kolom is afgerond op gehelen. De totale populatie is 2960. | |||||
| 7. | a. | VAN jonge vlieg NAAR oude vlieg is factor 2k, maar dat kan nooit meer dan 1 zijn, immers het zijn degenen die overleven. Dus 2k ≤ 1 dus k ≤ 0,5. | |||
| b. | Dat waren de 773 eitjes bij telling 22. Die zijn één telling later allemaal jong (en alle exemplaren die in telling 22 'jong' waren zijn een week later oud geworden) | ||||
| c. | van eitje naar jong:
alle 773 Dus bij telling 23 waren er 773 jonge vliegen en 994 -773 = 221 ouden Stel dat er bij telling 22 x jongen waren en dus 926 - x ouden Dat geeft bij telling 23 dan 7kx + 4k(926 - x) eitjes en dat moet gelijk zijn aan 887 Verder geeft dat bij telling 23 ook 2kx ouden en dat moet gelijk zijn aan 221 7kx + 4k(926 - x) = 887 ⇒ 7kx + 3704k - 4kx = 887 ⇒ 3kx + 3704k = 887 2kx = 221 geeft x = 221/2k en dat kun je invullen in de vorige vergelijking: 3k • 221/2k + 3704k = 887 331,5 + 3704k = 887 3704k = 555,5 k ≈ 0,15 en dat geeft voor telling 24: |
||||
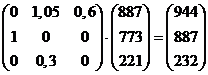 |
|||||
| Dat geeft 944 eitjes en 887 + 232 = 1119 vliegen, en dat klopt precies met de werkelijke aantallen. | |||||
| 8. | a. |
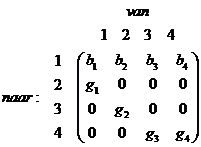 |
|||
| b. | De 302 km2
klasse 1 op t = 0 is op t = 1 overgegaan in 300 km2
klasse 2, dus g1 = 300/302 = 0,993 en dan is dus b1 = 0,007 De 284 km2 klasse 2 op t = 0 is op t = 1 overgegaan in 278 km2 klasse 3, dus g2 = 278/284 = 0,979 en dan is b2 = 0,021 |
||||
| c. | Uiteindelijk zal de vegetatie stabiel worden, en bestaan uit 19% klasse 1, 19% klasse 2, 18% klasse 3 en 44% klasse 4. | ||||
| d. |
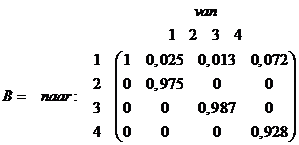 |
||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||