© h.hofstede (h.hofstede@hogeland.nl)

       
1. a. cosα = (-1 • -4 + 5 • -7)/(√26 • √65) = -31/41,11 = -0,754   ⇒    α = 138,9º  of  41,1º
       
  b. cosα = (0 • 6 + 4 • -4)/(√16 • √52) = -16/28,84 = -0,555   ⇒    α = 123,7º  of  56,3º
       
  c.
    cosα = (1 • -4 + 2 • 3)/(√5 • √25) = 2/11,18 = 0,179   ⇒   α = 76,7º
       
  d.
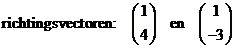    cosα = (1 • 1 + 4 • -3)/(√17 • √10) = -11/13,04 = -0,844   ⇒    α = 147,5º  of  32,5º
       
  e.
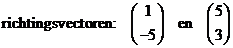    cosα = (1 • 5 + -5 • 3)/(√26 • √34) = -10/29,73 = -0,336   ⇒    α = 109,7º  of 70,3º
       
2. cosα = (-3 • 1 + a • 2)/(√5 • √(a² + 9))  =  ±1/2√3
-3 + 2a = ±1/2√3 • √(a2 + 9) • √5 
-6 + 4a = ±√15 • √(a2 + 9)
36 - 48a + 16a2 = 15a2 + 135
a2 - 48a - 99 = 0
a = (48 ± √2700)/2 = (48 ± 30√3)/2  =  24  ±  15√3    (ongeveer  -1,98 en  49,98)
       
3. a.
       
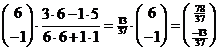  b.
       
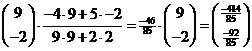4. Bereken de projectie van  OP op de richtingsvector van de lijn  (dat is 2 opzij, 7 omhoog):
 
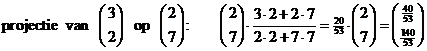  De projectie is het punt  P' =  (40/53, 140/53)
       
5.
 
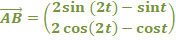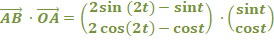  bij een hoek van 90º moet dat nul zijn:
(2sin(2t) - sint) • sint + (2cos(2t) - cost) • cost = 0
2sin(2t)sint - sin2t + 2cos(2t)cost - cos2t = 0

omdat sin2t + cos2t = 1 geeft dat:
2sin(2t)sint + 2cos(2t)cost = 1
sin(2t)sint + cos(2t)cost = 1/2

Maar die linkerkant is precies gelijk aan  cos(2t - t)
cos(2t - t) = 1/2
cost = 1/2
t = 1/3π + k2π  ∨  x = -1/3π + k2π
Op dit interval geeft dat t = 1/3π
       
6. Stel  P = (0, p)
 
  Die staan loodrecht op elkaar als het inproduct nul is:  -2 • 6 + (3 - p)•(7 - p) = 0
-12 + 21 - 3p - 7p + p2 = 0
p2 - 10p + 9 = 0
(p - 9)(p - 1) = 0
p = 9  ∨  p = 1
Dat zijn dus de punten  (0, 1) en (0, 9)
       
7. P = (0, 1/p)
Q = (π, -1/p)
R  = (2π, 1/p)
 
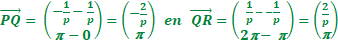  Voor loodrechte stand moet het inproduct nul zijn:
-2/p • 2/p + π • π = 0
-4/p² + π2 = 0
4/p² = π2
p2 = 4/π²
p = 2/π  ∨  p = -2/π
       
8. a. Kies een assenstelsel met de oorsprong in A
AF is de lijn  y = 0,5x
HD is de lijn  y = 1 - 1/3x
snijpunt:  0,5x =  1 - 1/3x
5/6x = 1
x = 6/5
dan is y = 3/5
AS is inderdaad de gevraagde vector,
       
  b.  
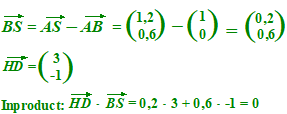    Het inproduct is NUL dus de vectoren staan loodrecht op elkaar.
       
9. a. De cosinussen van de hoeken tussen de richtingsvectoren moeten gelijk zijn.
   
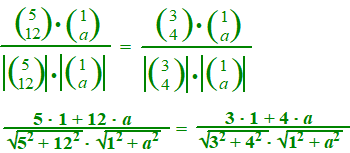    Kruislings vermenigvuldigen:
(5 + 12a) • 5 • √(1 + a2) = (3 + 4a) • 13 • √(1 + a2)
25 + 60a = 39 + 52a
8a = 14
a = 14/8 = 13/4
       
  b. Lijn m moet door het punt S gaan.
Voor S geldt:    29 + 5s = 3t  en   4 + 12s = 24 + 4t
de tweede geeft  t = -5 + 3s  en dat kun je invullen in de eerste:
29 + 5s = 3(-5 + 3s)
29 + 5s = -15 + 9s
44 = 4s
s = 11
Dan is S = (29 + 55, 4 + 132) = (84, 136)
Als dat op lijn m ligt moet gelden:   u = 84  en   b + u • a = 136 
b + 84 • 13/4 = 136
b = -11
       
       
       

© h.hofstede (h.hofstede@hogeland.nl)