|
|||||
| 1. | a. | leg een vlak V door de eerste lijn, evenwijdig aan de tweede: | |||
 |
|||||
| V is het vlak x - z = c en de steunvector invullen geeft x - z = 2 | |||||
| Kies punt P = (-2, -8, -2) van de
tweede lijn. Lijn l door P loodrecht op vlak V: |
|||||
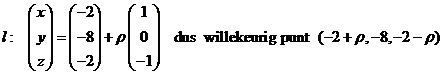 |
|||||
| Snijden van l
en V: -2 + ρ - (-2 -
ρ) = 2 ⇒ 0 +
2ρ = 2 ⇒ ρ = 1 De lengte van PP' is dus precies gelijk aan de lengte van de gebruikte normaalvector (immers ρ = 1) Dat is √(12 + 02 + 12) = √2 en dat is ook de afstand tussen de twee kruisende lijnen. |
|||||
| b. | leg een vlak V door de eerste lijn, evenwijdig aan de tweede: | ||||
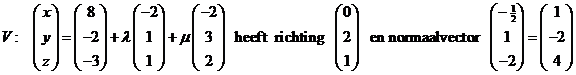 |
|||||
| V is het vlak
x - 2y + 4z = c en de steunvector
invullen geeft x - 2y + 4z = 0 Kies punt P = (7, -7, 0) van de tweede lijn. Lijn door P loodrecht op vlak V: |
|||||
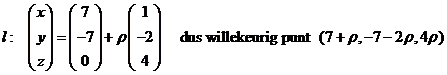 |
|||||
| Snijden van l
en V: (7 + ρ) - 2(-7 - 2ρ)
+ 4 • 4ρ = 0 ⇒
21 + 21ρ = 0 ⇒
ρ = -1 De lengte van PP' is gelijk aan de lengte van de gebruikte normaalvector. Dat is √(12 + 22 + 42) = √21 en dat is ook de afstand tussen de twee kruisende lijnen. |
|||||
| c. | leg een vlak V door de eerste lijn, evenwijdig aan de tweede: | ||||
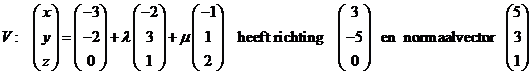 |
|||||
| V is het vlak 5x
+ 3y + z = c en de steunvector invullen geeft
5x + 3y + z = -21 Kies punt P = (0, -1, -3) van de tweede lijn. Lijn door P loodrecht op vlak V: |
|||||
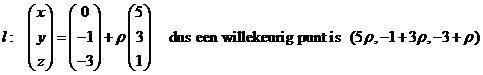 |
|||||
| Snijden van l
en V: 5 • 5ρ + 3(-1 + 3ρ)
+ -3 + ρ = -21 ⇒
-6 + 35ρ = -21 ⇒
ρ = -3/7 De lengte van PP' is gelijk aan 3/7 • de lengte van de gebruikte normaalvector. Dat is √(52 + 32 + 12) = √35 dus de afstand tussen de lijnen is 3/7√35 |
|||||
| d. | leg een vlak V door de eerste lijn, evenwijdig aan de tweede: | ||||
 |
|||||
| V is het vlak
-4x + 7y + z = c en de steunvector
invullen geeft -4x + 7y +
z = 70 Kies punt P(7, 5, -3) van de tweede lijn Lijn door P loodrecht op vlak V: |
|||||
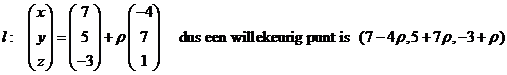 |
|||||
| Snijden van l
en V: -4(7 - 4ρ) + 7(5 + 7ρ)
+ (-3 + ρ) = 70 ⇒
4 + 66ρ = 70
⇒ ρ = 1 De lengte van PP' is gelijk aan de lengte van de gebruikte normaalvector. Dat is √(42 + 72 + 12) = √66 en dat is ook de afstand tussen de twee kruisende lijnen. |
|||||
| 2. | Kies D als oorsprong en de x-as langs DA. | ||||
| a. | A = (4, 0, 0) en M =
(0, 3, 5) B = (4, 6, 0) en E = (4, 0, 5) leg een v lak V door AM evenwijdig aan BE: |
||||
 |
|||||
| V is het vlak
15x - 20y + 24z = c en de steunvector
invullen geeft 15x - 20y + 24z = 60 Lijn door B(4, 6, 0) loodrecht op V: |
|||||
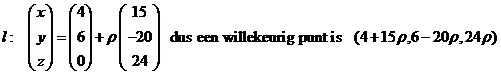 |
|||||
| Snijden van l
en vlak V: 15(4 + 15ρ) - 20(6 -
20ρ) + 24 • 24ρ
= 60 ⇒ -60 + 1201ρ
= 60 ⇒ ρ = -120/1201 De lengte van BB' is gelijk aan 120/1201 • de lengte van de gebruikte normaalvector. Dat is √(152 + 202 + 242) = √1201 dus de afstand tussen de lijnen is 120/1201 • √1201 ≈ 3,46. |
|||||
| b. | H = (0, 0, 5)
en B = (4, 6, 0) C = (0, 6, 0) en M = (0, 3, 5) leg een vlak V door HB evenwijdig aan CM: |
||||
 |
|||||
| V is het vlak
-15x + 20y + 12z = c en de steunvector
invullen geeft -15x + 20y + 12z = 60 Lijn door C(0, 6, 0) loodrecht op V: |
|||||
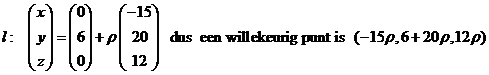 |
|||||
| snijden van l
en vlak V: -15 • -15ρ
+ 20 • (6 + 20ρ) + 12 • 12ρ
= 60 ⇒
120 + 769ρ = 60 ⇒ ρ = -60/769 De lengte van CC' is gelijk aan 60/769 • de lengte van de gebruikte normaalvector. Dat is √(152 + 202 + 122) = √769 dus de afstand tussen de lijnen is 60/769 • √769 ≈ 2,16 |
|||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||