© h.hofstede (h.hofstede@hogeland.nl)

 
1. basisvergelijking   x2 + (y - C1)2 -  C22  = 0                                   .....(1)
afgeleide:   2x + 2(y - C1) • y' = 0  ofwel   x + (y - C1) • y' = 0       .....(2)
tweede afgeleide:    1 + y' • y'  + (y - C1) • y''  = 0            ......(3)

in (2) en (3) komt al geen C2 meer voor.  Da's makkelijk.

(2)  geeft    (y - C1) = - x/y'
invullen in (3):   1 + (y')2  -  xy'' /y'  = 0
Dat is te herschrijven als  y' + (y')3 - xy'' = 0
       
2. basisvergelijking  y = asinx + bcosx    .......(1)
afgeleide:   y'  = acosx - bsinx      ......(2)
tweede afgeleide:   y''  = -asinx - bcosx    .....(3)

(1)  geeft   a = (y - bcosx)/sinx  en dat kun je invullen in (2) en (3)

Dat geeft
y' = (y - bcosx) • cosx/sinx  -  bsinx 
y''  = -y + bcosx - bcosx
De laatste is hem:    y'' + y = 0
       
3. basisvergelijking:   y = a/x + bx     .....(1)
afgeleide:   y' = -a/x² + b         .....(2)
tweede afgeleide:  y'' = -2a/x³       ....(3)

Uit (3) volgt   a = -0,5y'' x3
Dan volgt uit (2)  dat  b = y' + a/x²  =  y' - 0,5y''x
Samen invullen in (1):    y  = -0,5y'' x2 + y' x -  0,5y''x2 
Dat is wat netter te schrijven als:    y''x2  - y'x + y = 0   
       
4. a. y = Ae2x + Bex + C
y' = 2Ae2x + Bex      (1)
y'' = 4Ae2x + Bex     (2)
y''' = 8Ae2x + Bex    (3)
(2) - (1)  geeft  y'' - y' = 2Ae2x 
(3) - (1)  geeft  y''' - y' = 6Ae2x  
laatste min driemaal de vorige:   y''' - y' - 3y'' + 3y'  = 0  dus    y''' - 3y'' + 2y' = 0 
       
  b. y = Ax3 + Bx + C
y'  = 3Ax2 + B     ....(1)
y''  = 6Ax            ....(2)
y''' = 6A              ....(3)
(3)  geeft  xy''' = 6Ax  en als je daar (2) van af trekt geeft dat direct  xy''' - y''  = 0
       
  c. y = A√x + Bx
y' =  A/(2√x) + B     ....(1)
y'' =  -A/(4x√x)         .... (2)
(2) geeft  A = -4x√x • y''
dan geeft  (1):  B = y' + 2x
Samen geeft dat   y = -4x2 • y''  + xy'  + 2x2  
       
5. a. y = 2 + (2c - 2)x - c2  
y' = 2c - 2   geeft  c = 1 + 0,5y'
Invullen in de eerste vergelijking geeft  y = 2 + y'x - (1 + 0,5y')2 
y = 2 + y'x - 1 - y'  - 0,25(y')2
(y')2 + 4(1 - x)y'  + 4y  -  4 = 0 
       
  b. y = x2  - 2x + p  invullen geeft:
(2x - 2)2 + 4(1 - x)(2x - 2) + 4(x2 - 2x + p) - 4  = 0
4x2 - 8x + 4 + 8x - 8 - 8x2 + 8x + 4x2  - 8x + 4p - 4 = 0
-8 + 4p = 0
p = 2
       
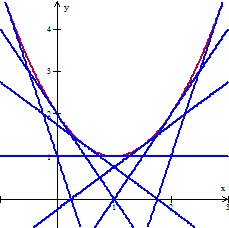
  c. y = x2  - 2x + 2 is een parabool (rood hieronder).
De krommen   y = 2 + (2c - 2)x - c2    zijn rechte lijnen (blauw hieronder) die raken aan die parabool  (de parabool is de omhullende van die rechte lijnen).
       
   

       
6. Algemene vergelijking:   y = ax2 + b
y' = 2ax
y''  = 2a
Dat geeft  xy'' = y'
       

© h.hofstede (h.hofstede@hogeland.nl)