|
|||||
| 1. | a. | y'' - 2y' - 3y = 0 karakteristieke vergelijking λ2 - 2λ - 3 = 0 (λ - 3)(λ + 1) = 0 λ = 3 ∨ λ = -1 Algemene oplossing y = A e3x + B e-x |
|||
| b. | y'' + 5y' - 6y = 0
karakteristieke vergelijking λ2 + 5λ - 6 = 0 (λ - 1)(λ + 6) = 0 λ = 1 ∨ λ = -6 Algemene oplossing y = A ex + B e-6x |
||||
| c. | y'' - 6y' + 9y = 0 karakteristieke vergelijking λ2 - 6λ + 9 = 0 (λ - 3)2 = 0 λ = 3 Algemene oplossing y = (Ax + B) e3x |
||||
| d. | 2y'' + 4y' + 2y = 0 y'' + 2y' + y = 0 karakteristieke vergelijking: λ2 + 2λ + 1 = 0 (λ + 1)2 = 0 λ = -1 Algemene oplossing y = (Ax + B) e-x |
||||
| e. | 6y'' + 6y' = -3y 6y'' + 6y' + 3y = 0 y'' + y' + 1/2y = 0 karakteristieke vergelijking λ2 + λ + 1/2 = 0 λ2 + λ + 1/4 + 1/4 = 0 (λ + 1/2)2 = -1/4 λ + 1/2 = 1/2i ∨ λ + 1/2 = -1/2i λ = -1/2 + 1/2i ∨ λ = -1/2 - 1/2i Algemene oplossing y = e-0,5x (Asin1/2x + Bcos1/2x) |
||||
| f. | y'' + 2y' = -5y y'' + 2y' + 5y = 0 karakteristieke vergelijking λ2 + 2λ + 5 = 0 λ2 + 2λ + 1 + 4 = 0 (λ + 1)2 = -4 λ + 1 = -2i ∨ λ + 1 = 2i λ = -1 - 2i ∨ λ = -1 + 2i Algemene oplossing: y = e-x (A cos2x + B sin2x) |
||||
| 2. | a. | y'' - 8y' + 16y =
0 met y(0) = 4 en y' (0)
= 2 karakteristieke vergelijking λ2 - 8λ + 16 = 0 (λ - 4)2 = 0 λ = 4 Algemene oplossing y = (A + Bx) e4x y(0) = 4 geeft 4 = A 1 dus A = 4 y'(0) = 2 geeft Be0 + (4 + B0)e0 4 = 2 dus B = -14 De oplossing is y = (4 - 14x) e4x |
|||
| b. | y'' + 5y' =
14y met y(0) = -4 en y'
(0) = 10 y'' + 5y' - 14y = 0 karakteristieke vergelijking: λ2 + 5λ - 14 = 0 (λ - 2)(λ + 7) = 0 λ = 2 ∨ λ = -7 Algemene oplossing y = A e2x + B e-7x y(0) = -4 geeft -4 = A + B dus A = -4 - B y'(0) = 10 geeft 2A - 7B = 10 eerste invullen in de tweede: -8 - 2B - 7B = 10 geeft B = -2 en dan is A = -2 De oplossing is y = -2e2x - 2e-7x |
||||
| c. | y'' + 2y' +
10y = 0 met y(0) = 1 en y'
(0) = 9 karakteristieke vergelijking λ2 + 2λ + 10 = 0 λ2 + 2λ + 1 + 9 = 0 (λ + 1)2 = -9 λ + 1 = 3i ∨ λ + 1 = -3i λ = -1 + 3i ∨ λ = -1 - 3i Algemene oplossing y = e-x (Acos3x + Bsin3x) y(0) = 1 geeft 1 = 1 (A + 0) dus A = 1 y' = -e-x(Acos3x + Bsin3x) + e-x(-3Asin3x + 3Bcos3x) y'(0) = 5 geeft 5 = -1 (1 + 0) + 1 (0 + 3B) dus B = 2 De oplossing is y = e-x(cos3x + 2sin3x) |
||||
| 3. | I'' + 60I' +
500I = 0 karakteristieke vergelijking λ2 + 60λ + 500 = 0 (λ + 10)(λ + 50) = 0 λ = -10 ∨ λ = -50 algemene oplossing I = A e-10t + B e-50t I(0) = 0 geeft 0 = A + B dus B = -A I'(0) = 40 geeft 40 = -10A - 50B eerste invullen in de tweede geeft 40 = 40A dus A = 1 dus B = -1 De oplossing is I(t) = e-10t - e-50t Voor het maximum is de afgeleide nul: I' = -10e-10t + 50e-50t = 0 10e-10t = 50e-50t e40t = 5 40t = ln5 = 1,609 t = 0,04 Dan is Imax = I(0,04) = 0,535 ampιre. |
||||
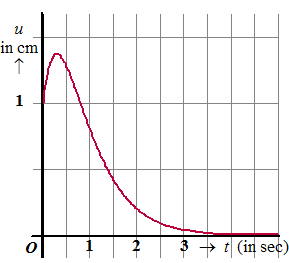
| 4. |
u'' + 4u' + 4u = 0 met u(0)
= 1 en u'(0) = 3. karakteristieke vergelijking: λ2 + 4λ + 4 = 0 (λ + 2)2 = 0| λ = -2 Algemene oplossing: u = (A + Bt) e-2t u(0) = 1 geeft 1 = (A + 0) 1 dus A = 1 u' = Be-2t + (A + Bt) -2e-2t u'(0) = 3 geeft 3 = B + (1 + 0) -2 dus B = 5 De oplossing is u(t) = (1 + 5t) e-2t |
||||
|
|
|||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||