|
|||||
| 1. | a. | y2
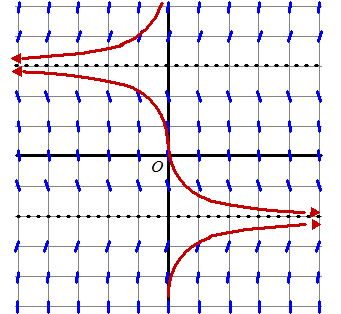
- y - 6 = 0 (y - 3)(y + 2) = 0 y = 3 ∨ y = -2 en dat zijn de horizontale asymptoten. |
|||
| b. | een paar isoklinen y = -4 geeft y' = -14 y = -3 geeft y' = -6 y = -1 geeft y' = -4 y = 0 geeft y' = -6 y = 1 geeft y' = -6 y = 2 geeft y ' = -4 y = 4 geeft y' = 6 y = 5 geeft y' = 14 enz. zie hiernaast |
|
|||
| c. | Het buigpunt vind je
bij maximale/minimale helling, dus als y' maximaal/minimaal is. y' is een dalparabool die minimaal is voor y = 1/2 De buigpunten liggen daarom op de lijn y = 1/2 |
||||
| 2. | a. | In (0, 5) is y' = -y2
+ 4y + p = -52 + 4 • 5 + p
= -5 + p Dat is positief (y stijgend) als p > 5 |
|||
| b. | y = 4x
- 8 snijdt de y-as in het punt (0, -8) Dan is y ' = -y2 + 4y + p = -(-8)2 + 4 • -8 + p = -64 - 32 + p = -96 + p Maar als de kromme de lijn y = 4x - 8 raakt moet de helling 4 zijn, dus -96 + p = 4 Dus p = 100. |
||||
| c. | Dan moet -y2
+ 4y + p overal kleiner dan nul zijn. Het is een bergparabool, en die is altijd kleiner dan nul als de discriminant negatief is: 42 + 4 • 1 • p < 0 16 + 4p < 0 geeft p < -4 |
||||
| 3. | a. | y' = y3
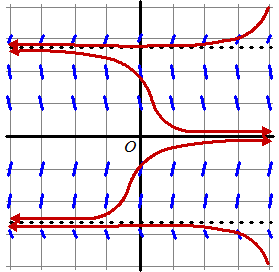
- 8y y ' = 0 voor y = 0, y = √8, y = -√8 een paar isoklinen: y = -4 geeft y' = -32 y = -2 geeft y ' = 8 y = -1 geeft y' = 7 y = 1 geeft y' = -7 y = 2 geeft y ' = -8 y = 3 geeft y' = 3 y = 4 geeft y' = 32 zoiets als hiernaast |
|
||
| b. | in y = ex
is de helling ook gelijk aan y' = ex ,
dus y' = y Dat geeft y = y3 - 8y y(y2 - 9) = 0 y = 0 ∨ y = 3 ∨ y = -3 y = ex geeft x= lny dus y = 0 en y = -3 kan niet, en y = 3 geeft het punt (ln3, 3) |
||||
| 4. | a. | y' = 0 geeft y
= ±1/2π,
±3/2π,
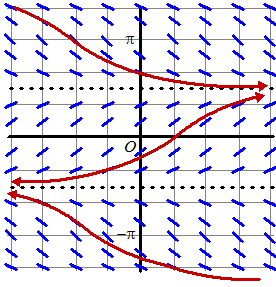
.... een paar isoklinen: y = 0 geeft y' = 1 y = ± 1/6π geeft y' = 1/2√3 y = ± 1/4π geeft y' = 1/2√2 y = ± 1/3π geeft y' = 1/2 y = ± 5/6π geeft y' = -1/2√3 y = ± 3/4π geeft y' = - 1/2√2 y = ± 2/3π geeft y' = - 1/2 zoiets als hiernaast |
|
||
| b. | 150
≈ 47,7π
dus dat is tussen 47,5π
en 48,5π Die zal als asymptoten de lijnen y = 47,5π en y = 48,5π hebben. Voor 〈1.5π, 2.5π〉 en 〈3.5π, 4.5π〉 en 〈5.5π, 6.5π〉 ...... zijn de krommen stijgend. Dus ook tussen 47,5π en 48,5π zijn de krommen stijgend. Deze kromme zal stijgend zijn. |
||||
| 5. | a. | y' = (y + 2)/(y - 1) = 0 geeft y = -2 en dat is horizontale asymptoot | |||
| b. | y = x
wordt geraakt als de helling 1 zou zijn. y' = 1 geeft (y + 2)/(y - 1) = 1 ⇒ y + 2 = y - 1 Þ 2 = -1 Dat kan niet, dus y = x wordt niet geraakt door een oplossingskromme. |
||||
| c. | Als y heel
groot wordt, dan is y + 2
≈ y en ook y - 1
≈ y Dus is y ' = (y + 2)/(y - 1) ≈ y/y = 1 De krommen krijgen bijna constante helling 1, dus lijken op rechte lijnen (met helling 1) |
||||
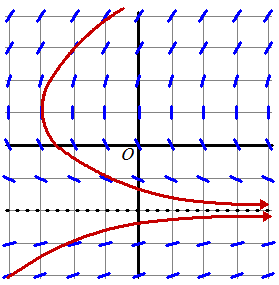
| d. | isoklinen: y = -4 geeft y' = 0,4 y = -3 geeft y' = 0,25 y = -1 geeft y' = -0,5 y = 0 geeft y ' = -2 y = 1 kan niet: verticale raaklijn y = 2 geeft y' = 4 y = 3 geeft y ' = 2,5 y = 4 geeft y' = 2 zoiets als hiernaast (aan de uiteinden gaat het naar helling 1 toe) |
|
|||
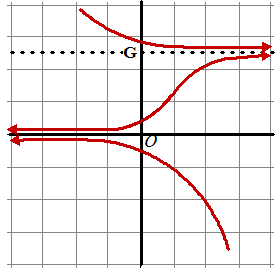
| 6. | y' = r • (1 - y/G)
• y y' = 0 geeft y = 0 ∨ y = G y' is een bergparabool (als r en G > 0), dus heeft een maximum bij y = 1/2G (midden tussen de nulpunten in). Daar hebben de oplossingskrommen dus maximale helling, dus een buigpunt. Tussen y = 0 en y = G zullen de oplossingskrommen een S-vorm hebben Boven y = G en onder y = 0 zijn de krommen voor grotere/kleinere y steeds sneller dalend. |
||||
|
|
|||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||