© h.hofstede (h.hofstede@hogeland.nl)

       
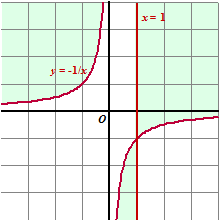
1. a. xydx + dy = xdy - dx
dx(xy + 1) = dy(x - 1)
dy/dx = (xy + 1)/(x - 1)

xy + 1 = 0  is de functie  y = -1/x
x - 1 = 0 is de lijn x = 1

De positieve lijnelementen zijn hiernaast groen gekleurd.

     
  b. dy/dx = (xy + 1)/(x - 1) = a
xy + 1 = ax - a
xy = ax - a - 1
y = a - a/x - 1/x

Dat is een rechte lijn als  -a/x - 1/x = 0  ofwel  a = -1  ⇒   de lijn y = -1
Het is ook een rechte lijn als x = 0  ⇒  de y-as
       
  c. bij x = 2 geldt  dy/dx = (y + 1)/(2 - 1)  = y + 1
bij x = 3  geldt: dy/dx = (3y + 1)/(3 - 1) = 1,5y + 0,5

Stel die lijn y = ax
dan gaat hij door (2, 2a)  en  (3, 3a)
Dat geeft hellingen  2a + 1  en   4,5a + 0,5
Die moeten gelijk zijn,  dus 2a + 1 = 4,5a + 0,5
0,5 = 2,5a  ⇒  a = -0,2
Het is de lijn y = -0,2x
       
  d. dy/dx = 0  geeft xy + 1 = 0  dus   y = -1/x
Snijden met een lijn y = ax  geeft  -1/x = ax
-1 = ax2
x2 = -1/a
x = √(-1/a)  ∨   x = -√(-1/a)
De afstand daartussen moet 3 zijn:   -√(-1/a) + 3 = √(-1/a)
3 = 2√(-1/a)
√(-1/a) = 1,5
-1/a = 2,25
a = -4/9
       
2.  xydx + dy = x2dy - xdx + dx
dx(xy + x - 1) = dy(x2 - 1)
dy/dx =  (xy + x - 1)/(x² - 1)

voor een rechte lijn door de oorsprong is  y = ax en  dy/dx = a
invullen:
a = (ax² + x - 1)/(x² - 1)
a(x2 - 1) = ax2 + x - 1
ax2 - a = ax2 + x - 1
a = 1 - x
Dan is  y = ax = (1 - x)x = x -  x2
Het is de parabool  y = x - x2
       
3. a. De helling moet 2 zijn:   dy/dx = (x² - y)/x = 2   ⇒  x2 - y = 2x

Verder is in de raakpunten y = 2x - 3
invullen geeft  x2 - 2x + 3 = 2x
x2 - 4x + 3 =  0
(x - 3)(x - 1) = 0
x = 3  ∨  x = 1
De raakpunten zijn   (1, -1)  en (3, 3)
De afstand daartussen is (met Pythagoras):  √(22 + 42) = √20 = 2√5  
       
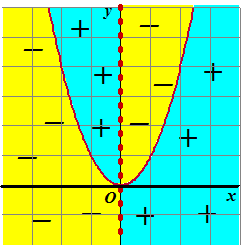
  b. De helling is nul als  x2 - y = 0  dat is op de parabool y = x2
De helling bestaat niet als x = 0, dat is de y-as.

Hiernaast zie je wanneer de helling plus of min is.
Voor een maximum moet de helling van plus naar min gaan als je naar rechts gaat, dus van blauw naar geel in de figuur.

Dat is alleen zo op de positieve y-as, maar daar bestaat de helling niet (is oneindig) dus is er nergens een maximum.
 
       

© h.hofstede (h.hofstede@hogeland.nl)