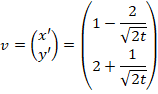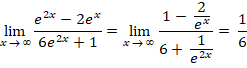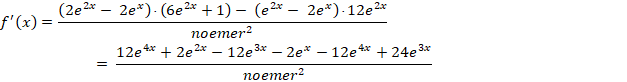© h.hofstede (h.hofstede@hogeland.nl)

 
1. a.

cirkel:  (x - 6)2 + y2 = 25
substitueer y = √(2x):   (x - 6)2 + 2x = 25
x2 - 12x + 36 + 2x = 25
x2 - 10x + 9 = 0

x = (10 ± 64)/2 = 9  ∨  1
x = 9 geeft punt  A(9, √18)
x = 1  geeft punt  B(1, √2)
AB2 = (√18 - √2)2 + (9 - 1)2  =  18 - 2√36 + 2 + 64 = 72
AB = √72 = 6√2
       
  b.

Teken lijn m vanaf N loodrecht op de grafiek van f
Stel dat die de grafiek van f snijdt in punt  S(p, √(2p))
De helling van f is   f ' =  1/√2p
 De helling van m is dan  -√(2p)  (loodrecht erop)
m is dus de lijn  y = -√(2p) • x + 6
Die moet door S gaan:  √(2p) = -√(2p) • p + 6
Intersect  geeft p = 2  dus  S = (2, 2)
Dan is  r = NS = √20 = 2√5
       
  c.
       
  d.

   

   

als t naar oneindig gaat, dan gaat v2  naar 5.
de limiet is dus √5
       
2. a.

    De asymptoot is de lijn y = 1/6 
 
   
   

De asymptoot is de lijn  y = 0
       
  b.

    12e3x + 2e2x - 2ex = 0
2ex(6e2x + ex - 1) = 0
6e2x + ex - 1 = 0
ex = (-1 ± Ö25)/12 = 1/3  of  -1/2
ex = 1/3  geeft  x = ln(1/3)
    Dan is y = -1/3  dus het minimum is  (ln(1/3), -1/3)
       
  c.

    6ey × x = ey - 2
ey(6x - 1) = -2
   

 
  d. De teller is nul als  e2x - 2ex = 0
ex(ex - 2) = 0
ex = 2   (dus  x = ln2)
Dan is de noemer ook nul als  6 × 4 + p = 0, dus als p = -24
   
   

ex = 2  geeft de perforatie  (ln2,  1/12)
       
      
   

   

 
    Het gemiddelde van beide y-coördinaten is 1/12 en dat is precies de y-coördinaat van de perforatie.
De bewering klopt dus.
       
 
       

© h.hofstede (h.hofstede@hogeland.nl)