|
|||||
| 1. | a. | e-1 + 2i
= e-1(cos2 + isin2) = -0,15 + 0,33i e2 + 2i = e2(cos2 + isin2) = -3,07 + 6,72i e2 + 6i = e2(cos6 + isin6) = 7,09 - 2,06i e-1 + 6i = e-1 (cos6 + isin6) = 0,35 - 0,10i |
|||
|
|
|||||
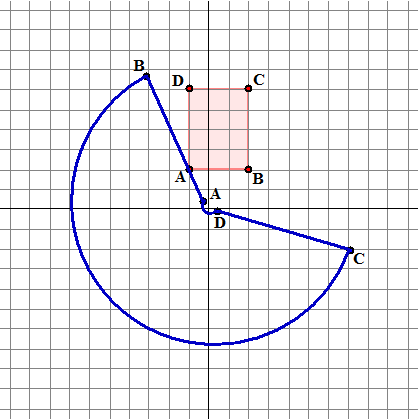
| De rode rechthoek verandert in de blauwe figuur. Horizontale lijnstukken worden delen van rechte lijnen door de oorsprong, verticale lijnstukken worden delen van cirkels (tegen de klok in als y in het origineel groter wordt). | |||||
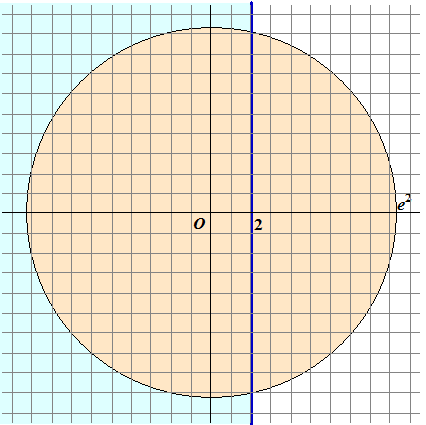
| b. | Het blauwe halve vlak (x < 2) verandert in het binnengebied van een cirkel met straal e2 | ||||
|
|
|||||
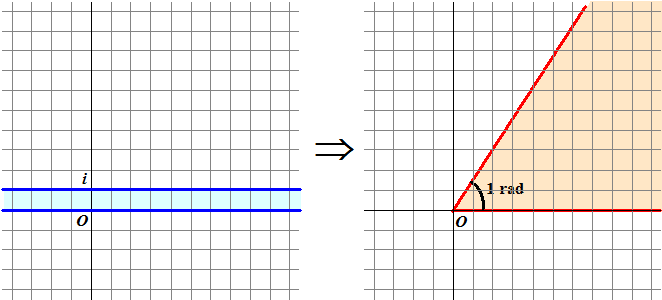
| c. | De blauwe strook links verandert in het rode vlakdeel rechts: | ||||
|
|
|||||
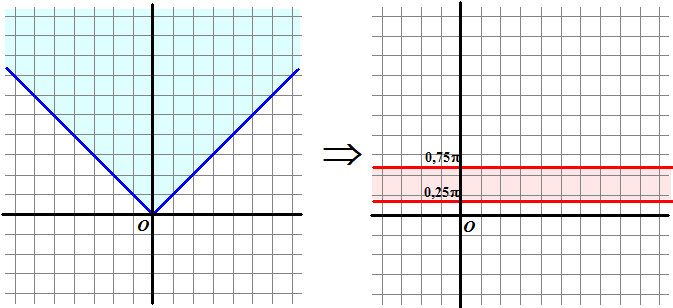
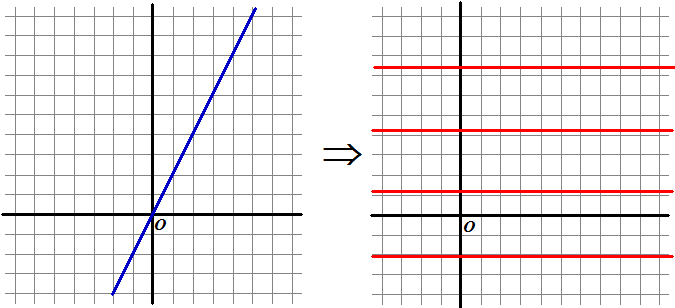
| 2. | a. | Het blauwe vlak tussen de hoeken 0,25π en 0,75π wordt een horizontale strook tussen y = 0,25π en y = 0,75π | |||
|
|
|||||
| b. | De lijn y = 2x
bestaat uit een stuk in het eerste kwadranten een stuk in het derde
kwadrant. Het deel in het eerste kwadrant verandert in een horizontale lijn op hoogte tan-1(2) = 1,11 rad, dus de punten op hoogte 1,11i Het deel in het derde kwadrant verandert in een horizontale lijn op hoogte 1,11 + π en dat is 4,25i (en verder natuurlijk nog alle horizontale lijnen op afstand 2π daarvan) |
||||
|
|
|||||
| 3. | z = r(cosφ
+ isinφ) ez = er(cosφ + isinφ) = ercosφ • eirsinφ = ercosφ • (cos(rsinφ) + isin(rsinφ) Rez = ercosφ • cos(rsinφ) en Imz = ercosφ • sin(rsinφ) mode par, en dan: X1T = e^(rcos(T)) • cos(rsin(T)) Y1T = e^(rcos(T)) • sin(rsin(T)) Neem voor r achtereenvolgens 0,5 en 1 en 2 |
||||
| 4. | a. | tanφ = a geeft φ = tan-1a dus de vergelijking is y = tan-1a | |||
| b. | De hoek is dan 3,25π en dat is hetzelfde als 1,25π dus dat is de halve lijn y = x voor x < 0 | ||||
| 5. | a. | Stel z = reiφ
= r(cosφ + isinφ)
dan is Imz = rsinφ
= 1 Dan is lnz = ln(reiφ) = lnr + iφ Het reële deel daarvan is lnr Dat is negatief als r < 1 maar dan kan nooit gelden dat rsinφ = 1 want sinφ is ook hoogstens gelijk aan 1. Dus het reële deel van lnz is altijd > 0 dus ligt lnz altijd rechts van de y-as. |
|||
| b. | Als Imz = 1
dan ligt z op de lijn (in het reële vlak) y =
1. Als nu ook nog x naar oneindig gaat (heel ver naar rechts) dan gaat de hoek φ naar nul. Dat betekent dat lnz = ln(reij) = lnr + iφ een imaginair deel heeft dat naar nul gaat, dus dat beeld gaat naar de x-as. |
||||
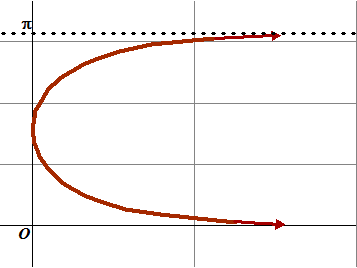
| c. | Zie vraag b) Nu gaat de hoek φ naar π, dus gaat het imaginaire deel van lnz naar π, dus dat wordt de lijn y = π. |
||||
| d. | z = i geeft lnz = lni = ln(e0,5πi) = 0,5πi | ||||
| e. |
 |
||||
| op de GR: Imz = 1 geeft rsinφ = 1 dus r = 1/sinφ lnz = lnr + iφ geeft dan lnz = ln(1/sinφ) + iφ mode par en dan xT = ln(1/sin(T)) en yT = T geeft de gevraagde beeldpunten. |
|||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||