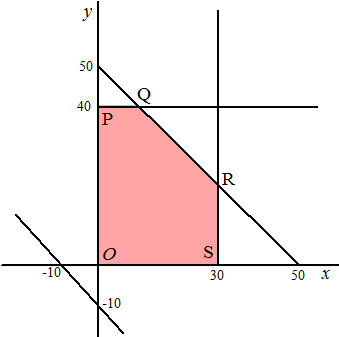© h.hofstede (h.hofstede@hogeland.nl)

       
1. Stel de te vervoeren hoeveelheden gelijk aan:
       
 
  A1 A2 A3
G1 x y 500 - x - y
G2 400 - x 400 - y 500 - (400 - x) - (400 - y)
= x + y  - 300
       
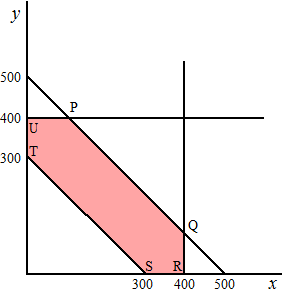
  Beperkende voorwaarden:
x  >  0
y >  0
400 - x  >  0  dus  x  <  400
400 - y  >  0  dus y  <  400
500 - x - y  >  0  dus  x + y  <  500
x + y - 300  >  0  dus  x + y  >  300

Kosten: 
K = 2 • 10 • x + 2 • 20 • y + 2 • 10 • (500 - x - y) + 2 • 10 • (400 - x) + 2 • 18 • (400 - y) + 2 • 20 • (x + y - 300)
K = 20x + 40y + 10000 - 20x - 20y + 8000 - 20x + 14400 - 36y  + 40x + 40y - 12000
K = 20x + 24y + 20400
       
 

       
  P = (100, 400)  en  KP = 32000
Q = (400,100)  en  KQ = 30800
R = (400, 0)  en  KR = 28400
S = (300, 0) en KS = 26400
T = (0, 300) en KT = 27600
U = (0, 400) en KU = 30000

De kosten zijn minimaal  26400,-  in punt  S.
Er moet  300 van  G1 naar A1 gaan en  200 van G1 naar A3
Er moet  100 van G2 naar A1 gaan  en  400 van G2 naar A2
       
2. de te vervoeren hoeveelheden:
 
  handelaar D handelaar E
fabriek A x 1000 - x
fabriek B y 1500 - y
fabriek C 2300 - x - y 1200 - (2300 - x - y)
=  x + y - 1100
       
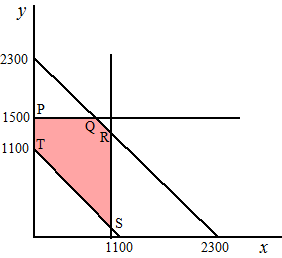
  voorwaarden:
x  >  0
y  >  0
1000 - x  >  0  dus  x  <  1000
1500 - y  >  0  dus  y  <  1500
2300 - x - y  >  0   dus  x + y  <  2300
x + y - 1100  >  0  dus  x + y  >  1100

Kostenfunctie:
K = 80x  + 100y + 102 • (2300 - x - y) +  215 • (1000 - x) + 108 • (1500 - y) +  68 • (x + y - 1100)
K = 80x + 100y + 234600 - 102x - 102y + 215000 - 215x + 162000 - 108y + 68x + 68y - 74800
K = 536800 - 169x - 134y  
       
 

       
  P = (0, 1500)  en  KP = 335800
Q:   y = 1500 en x + y = 2300  dus  Q = (800, 1500)  en  KQ = 200600
R:   x = 1000 en  x + y = 2300  dus  R = (1000, 1300)  en  KR = 193600
S:   x = 1000  en x + y = 1100 dus  S = (1000, 100)  en  KS = 354400
T = (0, 1100)  en  KT = 389400

De kosten zijn minimaal  193600 in Punt R:  
1000 van D naar A,  1300 van D naar B,   200 van E naar B,  1200 van E naar C
       
3. a. De te vervoeren hoeveelheden:  
   
  A B niet
AD x y 600 - x - y
Telegraaf 500 - x 700 - y 200 - (600 - x - y)
=  x + y - 400
       
   

       
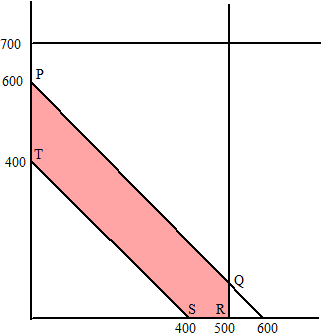
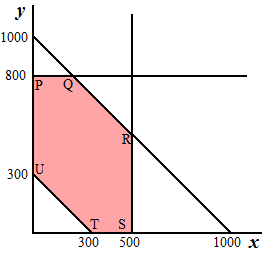
    Opbrengst:
O = 0,12x + 0,13y + 0,15(500 - x) + 0,15(700 - y)
O = 0,12x + 0,13y + 75 - 0,15x + 105 - 0,15y
O = 180 - 0,03x - 0,02y

P = (0, 600)  en  OP = 168
Q = (500, 100)  en  OQ = 163
R = (500, 0)  en  OR = 165
S = (400, 0)  en  OS = 168
T = (0, 400) en  OT = 172

O is maximaal  172,- in punt T:   400 AD naar B,  500 Telegraaf naar A,  300 Telegraaf naar B, 200 AD niet versturen.
       
  b. O is minimaal  163,- in punt  Q:   500 AD naar A, 100  AD naar B,   600 Telegraaf naar B, 200 Telegraaf niet.
       
4. De te vervoeren hoeveelheden:
 
  Assen Leeuwarden
Groningen x 30 - x
Drente y 40 - y
Friesland 50 - x - y 60 - (50 - x - y)
=  x + y + 10
       
 

       
  Kosten:
K = 6x + 2y + 18(50 - x - y) + 12(30 - x) + 19(40 - y) + 7(x + y + 10)
K = 6x + 2y + 900 - 18x - 18y + 360 - 12x + 60 - 19y + 7x + 7y + 70
K = 1390 -17x  - 28y

P(0, 40)  geeft  KP = 270
Q(10, 40)  geeft  KQ = 100
R(30, 20)  geeft KR = 320
S(30, 0)  geeft  KS = 850
O(0,0)  geeft  KO = 1390

K is minimaal  100  in punt Q:  10 van Groningen naar Assen,  40 van Drente naar Assen, 20 van Groningen naar Leeuwarden, 60 van Friesland naar Leeuwarden  
       
5. a. Het gewicht van het voedsel op tafel wordt "getransporteerd" naar gewicht op de schalen van de vrouwen.
       
  b. Na afloop zijn hun borden even vol dus iedere heeft 1500 gram voedsel gepakt.
Stel dat Els x gram wortels en y gram tarwekoekjes pakt, dan geldt voor de hoeveelheden:
     
   
  wortels tarwekoekjes rijst
Els x y 1500 - x - y
Harma 1000 - x 1000 - y 1500 - (1000 - x) - (1000 - y)
=  x + y - 500
       
   

       
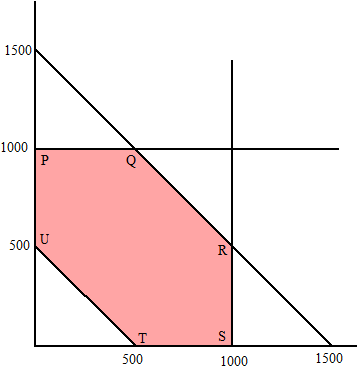
    Gewichtstoename:
G = 0,01x • 2 + 0,01y • 1 + 0,01 • (1500 - x - y) • 4 +  0,01(1000 - x) • 3 + 0,01(1000 - y)• 4 + 0,01(x + y - 500) • 6
G = 0,02x + 0,01y + 60 - 0,04x - 0,04y  + 30 - 0,03x + 40 - 0,04y + 0,06x + 0,06y - 30
G = 0,01x - 0,01y + 100

P (0, 1000) geeft  GP = 90
Q(500, 1000)  geeft  GQ = 95
R (1000, 500)  geeft  GR = 105
S (1000, 0)  geeft  GS = 110
T(500, 0)  geeft  GT = 105
U(0, 500)  geeft  GU = 95

De minimale gewichtstoename is 90 gram, en wordt bereikt in punt P(0, 1000).
Els neemt 1000 g tarwekoekjes.
Harma neemt 1000 g wortels.
Beiden nemen 500g rijst.
       
6. a. De te transporteren hoeveelheden:  
       
   
  slijterij supermarkt niet
lopende rekening x y 1000 - x - y
spaarrekening 500 - x 800 - y 1000 - (500 - x) - (800 - y)
= x + y - 300
       
   

       
  b. Kosten:
K = 0,005x + 0,01 • (500 - x) + 0,01y + 0,02 • (800 - y)
K = 0,005x + 5 - 0,01x + 0,01y + 16 - 0,02y
K = 21 - 0,005x - 0,01y

P = (0, 800)  en  KP = 13
Q = (200, 800) en KQ = 12
R = (500, 500)  en  KR = 13,50
S = (500, 0) en KS = 18,50
T = (300, 0) en KT = 19,50
U = (0, 300) en KU = 18

De minimale kosten zijn  12,- in punt Q
200 van de lopende rekening naar de slijterij,  800 van de lopende rekening naar de supermarkt,  300 van de spaarrekening naar de slijterij.
       
7. a. 140000 van Koeweit naar New York kost  0,38 • 140000 = 53200
100000 van Galveston naar New York  kost  0,10 • 100000 = 10000
60000 van Caracas naar New York kost 0,18 • 60000 = 10800
60000 van Koeweit naar Londen kost 0,35 • 60000 = 21000
50000 van Galveston naar Londen kost  0,22 • 50000 = 11000
40000 van Caracas naar Londen kost   0,25 • 40000 = 10000

In totaal is dat 116000 kosten
       
  b.

Naar
Van
New York Londen
Koeweit x 200000 - x
Galveston y 150000 - y
Caracas 300000 - x - y 150000 - (200000 - x) - (150000 - y) =
x + y  - 200000
       
    Kosten:
K = 0,38x + 0,10y + 0,18(300000 - x - y) + 0,35(200000 - x) + 0,22 • (150000 - y) + 0,25 • (x + y - 200000)
K = 0,38x + 0,10y + 54000 - 0,18x - 0,18y + 70000 - 0,35x + 33000 - 0,22y + 0,25x + 0,25y - 50000
K = 107000 + 0,10x - 0,05y 
       
   

       
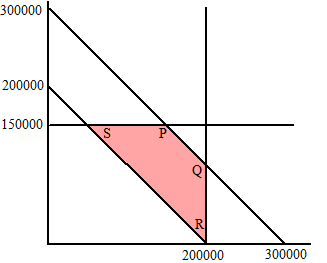
    P = (150000, 150000) en  KP = 114500
Q = (200000, 100000)  en  KQ = 122000
R = (200000, 0)  en KR = 127000
S = (50000, 150000)  en  KS = 104500

De kosten zijn minimaal  104500  in punt S
50000 van Koeweit naar New York, 150000 van Koeweit naar Londen
150000 van Galveston naar New York. 
100000 van Caracas naar New York.
       
  c.
  D1 D2 D3 D4 D5 D6 D7 D8
K1                
K2                
K3                
K4                
K5                
K6                
       
    Op de grijze vakjes moeten variabelen staan, dan liggen die aan de rand daarna vast.
Dat zijn 7 • 5 = 35 variabelen.
       

© h.hofstede (h.hofstede@hogeland.nl)