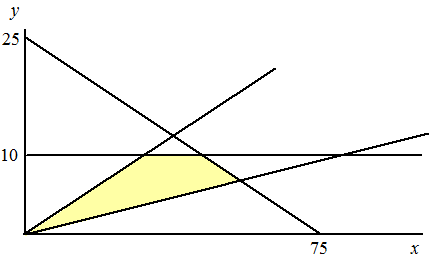© h.hofstede (h.hofstede@hogeland.nl)

       
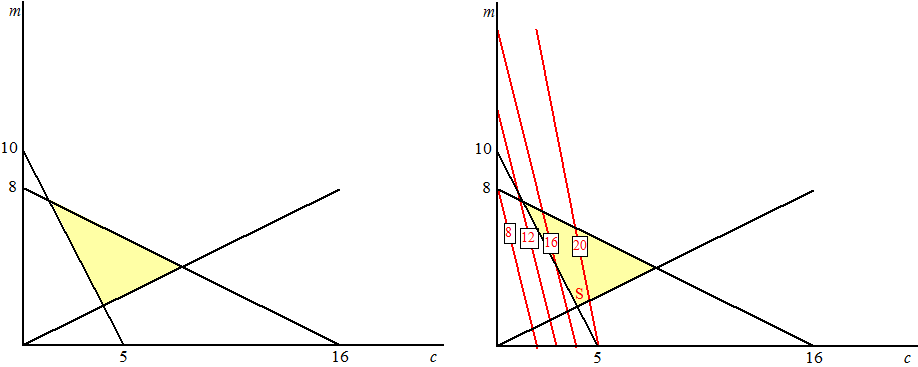
1. a. Stel dat ik m moorkoppen en c chocoladetaartjes neem

maximaal 1600 calorieλn:  200m + 100c  ≤ 1600 
400 gram voedsel:  40m + 80c  ≥  400
"minstens de helft":  m  ≥  0,5c
logisch:  m, c  ≥  0

Doelstellingsfunctie:   K = m + 4c  moet minimaal

Dat geeft het volgende gebied links met een paar niveaulijnen rechts:
       

       
    Daar ergens tussen de lijnen van K = 28 en K = 40  loopt de lijn van minimale kosten door punt S.
S is het snijpunt van   m = 0,5c  en   40m + 80c = 400
invul van de eerste in de tweede geeft  40 • 0,5c + 80c= 400  en dat geeft  c =  4
Dan is m = 0,5c = 2  en  K = m + 4c =  18
       
  b. Als de prijs van c verlaagt, gaan de niveaulijnen steeds vlakker lopen
Het minimum komt in een ander hoekpunt te liggen op het moment dat de niveaulijn evenwijdig aan de lijn 
200m + 100c =  1600   loopt
Dat is hetzelfde als  m + 0,5c = 8
De prijs van de chocoladetaartjes is dus 0,5 geworden (en de  minimale kosten zijn 8)
       
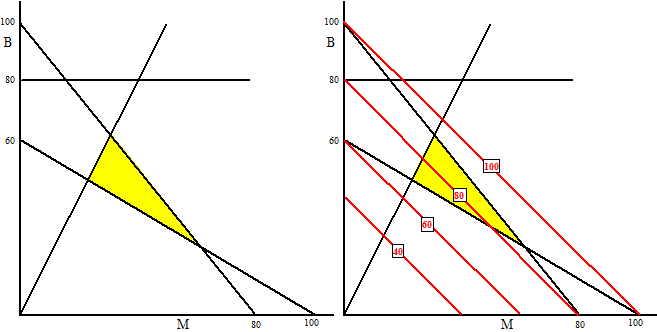
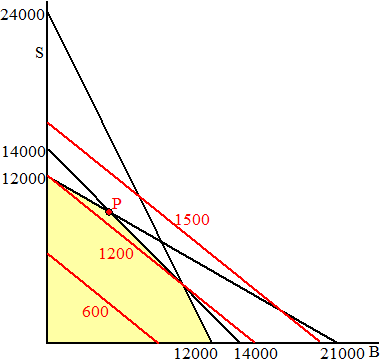
2. Stel dat ik M marsen en B bountys koop.

hoogstens 52,-  geeft dan  0,65M + 0,52B  ≤  52
calorieλn:   390M + 650B ≥  39000
maximaal aantal bountys:   B ≤ 80
extra voorwaarde  M ≤ 0,5B
logisch:  M, B ≥ 0

Doelstellingsfunctie: aantal stuks  S = M + B  moet maximaal
Dat geeft het volgende gebied met wat niveaulijnen rechts
       
 

       
  Het hoogste aantal snoepgoed zit bij het punt bovenin het toelaatbare gebied.
Dat is het snijpunt van   0,65M + 0,52B  =  52  en   M = 0,5B.
tweede invullen in de eerste:  0,65 • 0,5B + 0,52B = 52.
0,845B = 52.
B = 61,53
Dan is M = 30,76
Het maximum is (geheel aantal)  61 Bounty's en 30 Marsen, dus 91 stuks snoep.
       
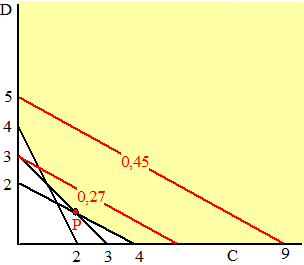
3. voorwaarden:
vitamine B:  C + D ≥ 3
vitamine K:  C + 2D ≥ 4
vitamine C:  10C + 5D  ≥ 20
logisch:  C, D  ≥ 0

doelstellingsfunctie:  K = 0,09D + 0,05C  moet minimaal
       
 

       
  K is minimaal in punt P:  het snijpunt van   C + D = 3  en   C + 2D = 4
De eerste geeft  C = 3 - D en dat kun je invullen in de tweede:  3 - D + 2D = 4  geeft dan  D = 1  en dan is  C = 2
       
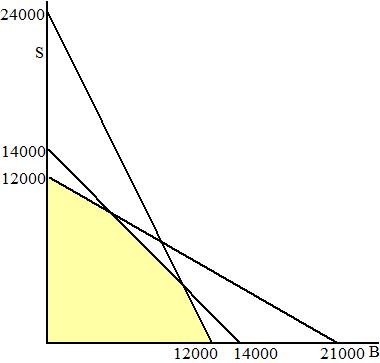
4. a. Stel dat hij B  rollen boerenbeschuit en S rollen Sesambeschuit maakt.

kneedmachine:  B/180  + S/100  ≤ 120  ofwel  5B + 9S  ≤  108000
oven:  B/300 + S/600  ≤ 40   ofwel  2B + S  ≤  24000
inpakmachine:  B/200 + S/200  ≤ 70  ofwel  B + S ≤  14000
logisch:  B, S  ≥ 0

Dat geeft het volgende toelaatbare gebied:
   

     
  b. O = 0,08B + 0,10S  geeft de volgende soort niveaulijnen:
   

     
    De maximale opbrengst wordt gehaald in punt P en dat is het snijpunt van  5B + 9S  =  108000  en   B + S = 14000
Uit de tweede volgt  B = S - 14000 en dat kun je invullen in de eerste:
5(14000 - S) + 9S = 108000
70000 - 5S +  9S = 108000
4S = 38000
S = 9500  en dan is  B = 14000 - 9500 = 4500
De opbrengst is dan O = 0,08 • 4500 + 0,10 • 9500 = 1310  
       
  c. In punt P is de lijn   2B + S  = 24000  niet gebruikt, daar liggen we nog een stukje onder.
Dat betekent dat de oven nog onderbezet is.
Die wordt  4500/300 + 9500/600 = 30,83 uur gebruikt van de maximale 40 uur, dus dat is  (40 - 30,83)/40 • 100% = 23% van de beschikbare tijd niet gebruikt.
       
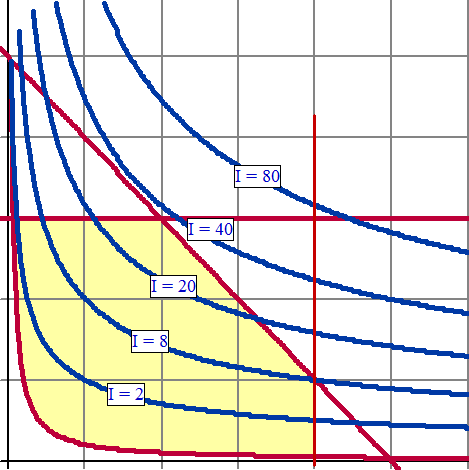
5. a. De breedte van de kasten moet passen:  a + b  ≤ 5   (schuine lijn rechtsboven)
De lengte van de kasten moet passen:  a  ≤  4   (rechter verticale lijn)
De vloeroppervlakte:  2ab  ≥  0,4   (onderste kromme lijn)
De hoogte van de kasten moet passen:  b  ≤  3   (bovenste horizontale lijn)
       
  b.

       
    De maximaal haalbare inhoud is net iets minder dan 40, want die niveaulijn ligt net buiten het toelaatbare gebied.
       
  c.

       
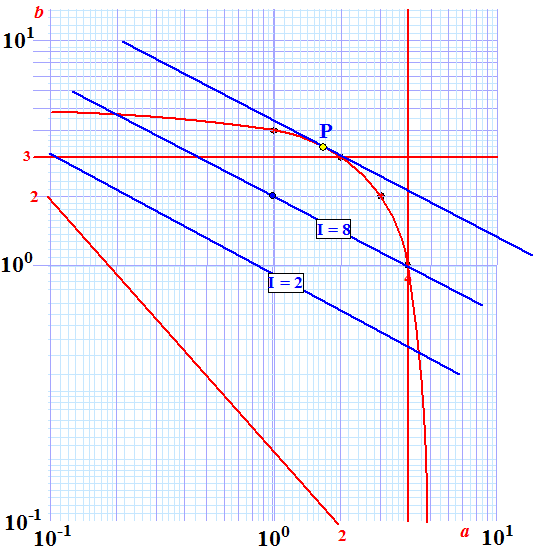
    De rode lijnen zijn de grenslijnen, de blauwen de niveaulijnen
Het maximum vinden we in punt P ongeveer bij a = 1,7  en  b = 3,1
       
  d. a + b = 5  geeft  a = 5 - b
I = 2ab2 =  2 • (5 - b) • b2 = 10b2 - 2b3
I is maximaal als I' = 0   dus  20b - 6b2 = 0
b(20 - 6b) = 0
b = 0  ∨   b = 20/6 = 31/3
Dat laatste is het maximum, dus dan is  b = 31/3  en  a = 12/3  en   I = 2ab2 = 37,04 m3
       
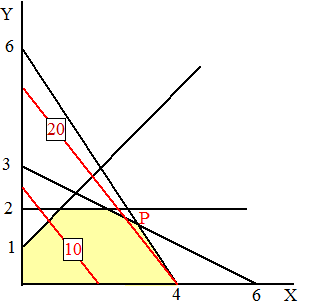
6. zuur:   6X + 4Y  ≤ 24
base:  X + 2Y  ≤  6
maximaal 2:   Y  ≤ 2
hoogstens ιιn meer Y dan X:   Y ≤ X + 1
logisch:  X, Y  ≥ 0

doelstellingsfunctie: O = 5X + 4Y
Toelaatbaar gebied met twee niveaulijnen:
       
 

       
  O is maximaal in punt P:  snijpunt van  6X + 4Y = 24  en  X + 2Y = 6
Uit de tweede volgt  X = 6 - 2Y en dat kun je invullen in de eerste:    6(6 - 2Y) + 4Y = 24
36 - 12Y + 4Y = 24
12 = 8Y
Y = 1,5  en dan is  X = 6 - 2Y = 3
O  is maximaal   5 • 3 + 4 • 1,5 = 21
       
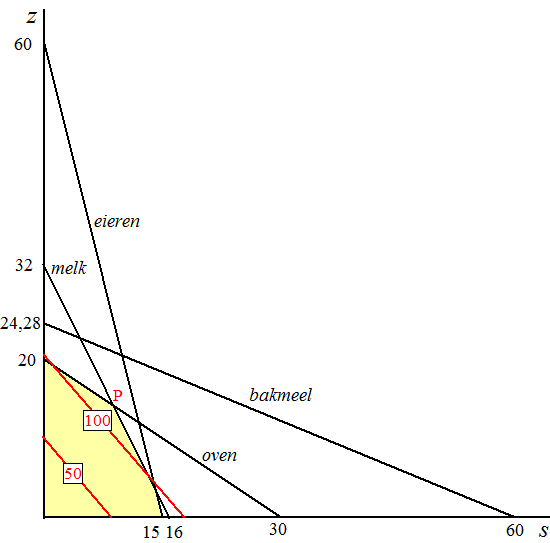
7. a Stel ze maakt  z zandtaart en s schuimgebak:

bakmeel:  700z + 300s  ≤  17000
melk:  0,5z + s  ≤  16
eieren:  z + 4s  ≤  60
logisch:  z, s  ≥ 0
       
  b. Het totale aantal oven-uren is 60  dus  2s + 3z  ≤  60
       
  c. W = opbrengst - kosten 
Opbrengst = 10z + 10s
Kosten = oven + bakmeel + eieren + melk = (2s + 3z)•1 + (0,7z + 0,3s)•2 + (z + 4s) • 0,20 + (0,5z + s) • 1 = 4,4s + 5,1z
W = 10z + 10s - 4,4s - 5,1z = 4,9z + 5,6s
       
  d.

       
    W is maximaal in punt P:  het snijpunt van  0,5z + s = 16  en   2s + 3z = 60
Uit de eerste volgt  s = 16  -0,5z en dat kun je invullen in de tweede:  2(16 - 0,5z) + 3z = 60
32 - z + 3z = 60
2z = 28
z = 14  en dan is  s = 16 - 0,5 • 14 = 9  en dan is  W = 4,9 • 14 + 5,6 • 9 = 119
De vrouw moet  14 zandtaarten en 9 schuimtaarten gaan bakken
       
8. a. totaal 75 "auto's":   x + 3y  ≤  75
maximum voor bussen:   y  ≥  10
auto's niet minder dan driemaal bussen:   x  ≥  3y
auto's niet meer dan 8 maal bussen:  x  ≤  8y
logisch:  x, y  ≥  0  en geheel.

Dat geeft (de roosterpunten uit) het volgende gebied:
       
   

       
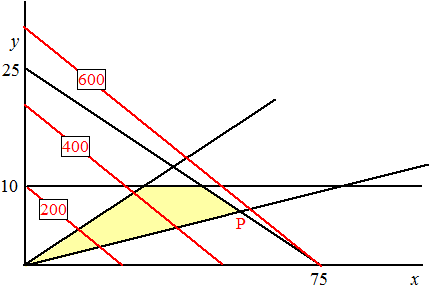
  b. Doelstellingsfunctie:   O  = 8x + 20y  en hieronder staan een paar niveaulijnen:  
       
   

       
    De maximale opbrengst is in punt P:   snijpunt van  x = 8y  en    x + 3y = 75
eerste invullen in de tweede:   8y + 3y = 75
11y = 75
y = 6,81  en dan is x = 54,54
Het roosterpunten het dichtst daarbij is  (54, 7)  (die ligt nog net op x + 3y = 75)
Dat geeft opbrengst  8 • 54 + 20 • 7 = 572
       
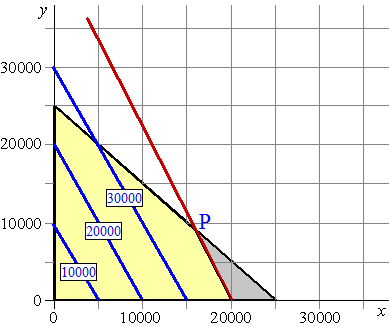
9. a. De grenslijn uit deze figuur gaat door  (0, 25000)  en  (25000, 0) en het gebied voldoet dus aan  x + y  <  25000
Dat wil zeggen dat er voor het tuincentrum minstens 36000 - 25000 = 11000 m2 moet overblijven
       
  b. •  x  m2 park kost  105x  gulden
•  36000 - x - y   tuin  levert  (36000 - x - y ) •  300 = 10800000 - 300x - 300y  op
•  y volkstuinen levert  120y op
•  aankopen van 36000 m2 grond kost  36000p

Dan moet gelden:    10800000 - 300x - 300y + 120y  ≥  105x + 36000p
405x + 180y  ≤ 10800000 - 36000p  
Alles delen door 45:     9x + 4y  ≤  240000 - 800p
       
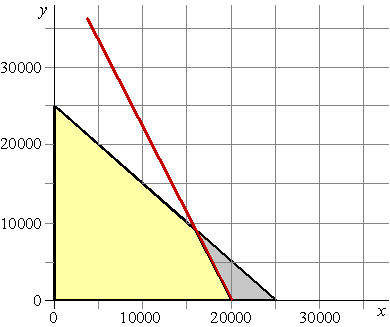
  c. 9x + 4y  ≤  240000 - 800 • 75
9x + 4y  ≤  180000   gaat door bijv.   (0, 45000)  en  (20000, 0)  en  (10000, 22500)
       
   

       
  d. W = 2x + y   geeft een paar niveaulijnen hieronder:  
       
   

       
    Maximale W wordt bereikt in punt P:  het snijpunt van  9x + 4y = 180000  en   x + y = 25000  
Uit de tweede vologt  y = 25000 - x en dat kun je invullen in  de eerste:  9x + 4(25000 - x) = 180000
9x + 100000 - 4x = 180000
5x = 80000
x = 16000  en dan is y = 9000   (en dan is de maximale W gelijk aan  2 • 16000 + 9000 = 41000)
       
10. a. g:  3 + 2 + 2 + 2 + 2 = 11 dus  g ≤ 11.

de totale capaciteit is minstens 1000.
capaciteit van g treinen is 80g
capaciteit van b boten is 50b
dus moet gelden  80g + 50b ≥ 1000
delen door 10 geeft de gevraagde vergelijking.
       
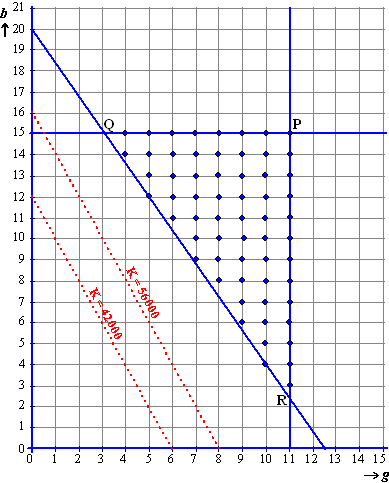
  b. De voorwaarden zijn de blauwe lijnen hieronder, en het gezochte gebied is de blauwe driehoek.
Maar omdat b en g gehele getallen zijn, moet je alleen de roosterpunten binnen deze driehoek nemen.

Zie tekening. Het zijn de blauwe stippen.
       
   

       
  c. K = 7000g + 3500b zijn de kosten.
Hierboven zijn twee isolijnen getekend.
Je ziet dat de kosten zo laag mogelijk zijn als die lijnen zover mogelijk naar links geschoven zijn.
Dat is zo als de isolijn precies door de punten (4,14) en (5,12) gaat.

De kosten zijn dus minimaal als g = 4 en b = 14  of als  g = 5 en  b = 12 (en die kosten zijn trouwens 77000)
       

© h.hofstede (h.hofstede@hogeland.nl)