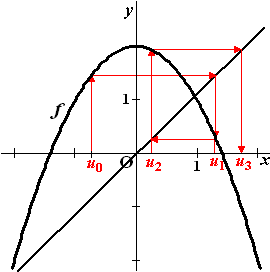|
|||||
| 1. | a. | un = 0,8un
- 1 + 2 met u0 = 1 E = 0,8E + 2 0,2E = 2 E = 10 De rij convergeert neem bijv. un - 1 = 9,9 dan is un = 9,92 en dat ligt dichter bij de evenwichtswaarde 10. |
|||
| b. | un = un- 12
- 2 met u0 = 0 E = E2 - 2 E2 - E - 2 = 0 (E - 2)(E + 1) = 0 E = 2 ∨ E = -1 in de buurt van E = 2 divergeert de rij neem bijv. un - 1 = 1,9 dan is un = 1,61 en dat ligt verder van de evenwichtswaarde af. in de buurt van E = -1 divergeert de rij ook neem bijv. un - 1 = -0,9 dan is un = -1,19 en dat ligt verder van de evenwichtswaarde af. Voor u0 = 0 gaat de rij naar 2 (die waarde wordt voor n = 2 zelfs al bereikt!) |
||||
| c. | un = un
- 13 met u0 =
-1,5 E = E3 E3 - E = 0 E(E2 - 1) = 0 E = 0 ∨ E = 1 ∨ E = -1 in de buurt van E = 0 convergeert de rij neem bijv. un - 1 = 0,1 dan is un = 0,001 en dat ligt dichter bij de evenwichtswaarde. in de buurt van E = ±1 divergeert de rij neem bijv. un - 1 = ±0,9 dan is un = ±0,729 en dat ligt verder van de evenwichtswaarde af. Voor u0 = -1,5 divergeert de rij naar een oneindig negatieve waarde |
||||
| d. | un = 2,5√(un -
1- 1) met u0
= 1 E = 2,5√(E - 1) E2 = 6,25(E - 1) E2 - 6,25E + 6,25 = 0 ABC-formule: E = (6,25 ±√(14,0625))/2 = 5 of 1,25 In de buurt van E = 5 convergeert de rij neem bijv. un - 1 = 4,9 dan is un = 4,994 en dat ligt dichter bij de evenwichtswaarde. in de buurt van E = 1,25 divergeert de rij neem bijv. un - 1 = 1,249 dan is un = 1,247 en dat ligt verder van de evenwichtswaarde af. Voor u0 = 1 bestaat de rij vanaf n = 2 al niet meer omdat je een negatieve wortel krijgt. |
||||
| 2. | a. | E = 0,8 + 0,2E2
0,2E2 - E + 0,8 = 0 E2 - 5E + 4 = 0 (E - 4)(E - 1) = 0 E = 4 ∨ E = 1 De dekpunten zijn dus (1,1) en (4,4) |
|||
| b. |
|
||||
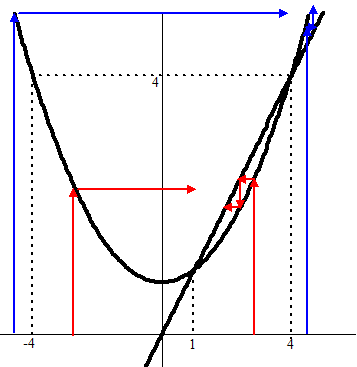
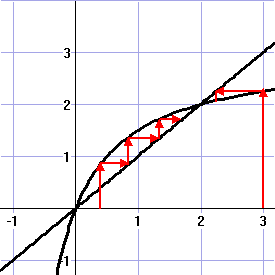
| Hierboven zie je een
aantal gevallen. De rode pijlen lopen naar (1,1) toe, de blauwen niet. Voor startwaarden -4 < u0 < 4 convergeert de rij naar (1,1) |
|||||
| c. | Zie de figuur bij b) . De rij convergeert NOOIT naar (4,4) maar loopt ervan weg. | ||||
| 3. | a. | un = √(un - 1) | |||
| b. | E =
√E E2 = E E2 - E = 0 E(E - 1) = 0 E = 1 ∨ E = 0 In de buurt van E = 1 convergeert de rij neem bijv. un - 1 = 0,9 dan is un = 0,94 en dat ligt dichter bij de evenwichtswaarde. In de buurt E = 0 divergeert de rij neem bijv. un - 1 = 0,1 dan is un = 0,32 en dat ligt verder van de evenwichtswaarde af. |
||||
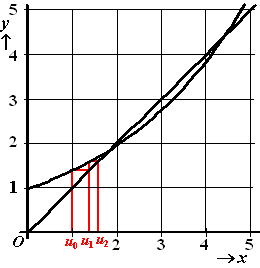
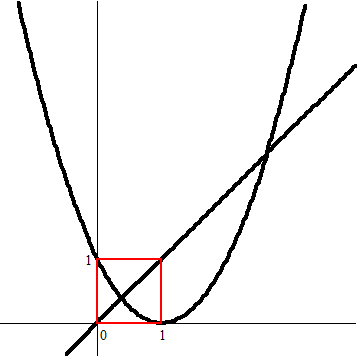
| 4. | a. | Zie de figuur hiernaast. Het enige "vierkantje" met twee hoekpunten op de parabool en twee op de lijn y = x dat je kunt tekenen lijkt bij x = 0 en x = 1 te zitten. |
 |
||
| b. | un + 1
= (un - 1)2 un + 2 = (un + 1 - 1)2 = ((un - 1)2 - 1)2 Als de rij alterneert dan moet gelden un + 2 = un dus un = ((un - 1)2 - 1)2 Y1 = X Y2 = ((X - 1)^2 - 1)^2 intersect geeft X = 2,618 ∨ X = 1 ∨ X = 0,382 ∨ X = 0 u0 = 2,618 en u0 = 0,382 zijn de dekpunten waarbij de rij monotoon is. u0 = 0 en u0 = 1 zijn de gevallen waarin de rij alterneert |
||||
| 5. | a. | Voor
de limiet L geldt un = un
-1 = L dus L = 1/(2 - L) dan is L(2 - L) = 1 ⇒ 2L - L2 = 1 ⇒ L2 - 2L + 1 = 0 ⇒ (L - 1)2 = 0 ⇒ L = 1 |
|||
| b. | Als un
= (n + 1)/(n + 2) dan is
un -1 = n/(n +
1) (vervang elke n door n
- 1) Invullen in de recursievergelijking: |
||||
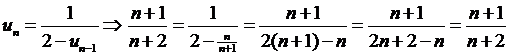 |
|||||
| 6. | a | Ga
steeds naar de grafiek van ax en dan weer naar de lijn
y = x zoals hiernaast. Dat levert op de x-as de gezochte u-waarden. |
|
||
| b. | Het
grensgeval zal zijn als de twee grafieken y = x
en y = ax elkaar raken. Dan zijn hun hellingen gelijk: 1 = ax • lna Verder gaan ze door het zelfde punt: x = ax Deze invullen in de regel erboven geeft 1 = x • lna ofwel lna = 1/x dus a = e1/x x = ax geeft dat x = (e1/x)x = e en dan is a = e1/e |
||||
| 7. | a. |
|
|||
| b. | De rij
is constant als f(un - 1) = un
- 1, dus als f(x) = x. 2 - x2 = x ⇒ x2 + x - 2 = 0 ⇒ (x - 1)(x + 2) = 0 ⇒ x = 1 ∨ x = -2 Dat zijn de gezochte startwaarden. |
||||
| c. | un
= a, dan is un + 1 = b = 2 - a2 dan is un + 2 = 2 - b2 = 2 - (2 - a2 )2 en dat moet gelijk zijn aan a 2 - (2 - a2 )2 = a Y1 = X en Y2 = 2 - (2 - x2 )2 window bijv. Xmin = -3, Xmax = 3, Ymin = -4, Ymax = 4 intersect levert X = -2 ∨ X ≈ -0,618 ∨ X = 1 ∨ X ≈ 1,618 De waarden waarvoor a en b van elkaar verschillen zijn a = 0,618 en a = 1,618 |
||||
| 8. | a. | E = 1,6 + 0,1E2
0,1E2 - E + 1,6 = 0 E2 - 10E + 16 = 0 (E - 8)(E - 2) = 0 E = 8 ∨ E = 2 De dekpunten zijn (2,2) en (8,8) |
|||
|
|
|||||
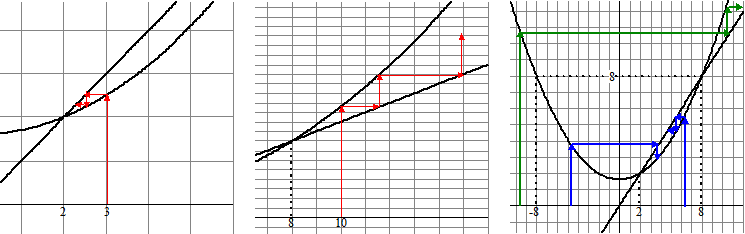
| b. | Voor u1
= 3 convergeert de rij naar 2 (figuur links) Voor u1 = 10 divergeert de rij (figuur midden) |
||||
| c. | Voor waarden -8 < u1 < 8 convergeert de rij naar het punt (2,2): figuur rechts. | ||||
| d. | In de buurt van het grootste dekpunt loopt de webgrafiek "weg" van dat punt. Dat komt omdat de parabool daar steiler loopt dan de lijn y = x | ||||
| 9. | a. | Teken de
lijn y = x in de figuur. Die heeft snijpunten (0,0) en
(2,2) met de grafiek van f. Aan de figuur hiernaast zie je dat als we willekeurig ergens beginnen, de webgrafiek naar het punt (2,2) loopt, dus de rij convergeert naar 2. ((2,2)is een attractor) De enige uitzondering is als we in x = 0 beginnen: dan blijven we daar ook. Conclusies: voor v0 > 0 convergeert de rij naar 2 voor v0 = 0 convergeert de rij naar 0 |
|
||
| b. | De
functie bestaat niet voor x = -1. Dus als er ergens in de rij -1
voorkomt zijn de volgende termen niet meer gedefinieerd. Hoe kan er -1
voorkomen? Als we beginnen bij v0 = -1. Als we beginnen bij een getal waarvan de functiewaarde -1 is (want dan wordt v1 = -1), dus als 3 - 3/(x+ 1) = -1 ⇒ 3/(x + 1) = 4 ⇒ x + 1 = 0,75 ⇒ x = -0,25 dus v0 = 0,25 Als we beginnen bij een getal waarvan de functiewaarde -0,25 is (want dan wordt v1 = -0,25 en v2 = -1) dus als 3 - 3/(x+ 1) = -0,25 ⇒ 3/(x + 1) = 3,25 ⇒ x + 1 = 12/13 ⇒ x = -1/13 dus v0 = -1/13 enzovoort..... |
||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||