© h.hofstede (h.hofstede@hogeland.nl)

       
1. 35, 35, 35, 38, 42, 42, 42, 42, 56, 67, 67, 68, 70.
       
  Het gemiddelde is  49,154

De spreidingsbreedte is de grootste min de kleinste. Dat is  70 - 35  = 35

Q1 is nummer 3-4 van de 13 en dat is  (35 + 38)/2 = 36,5
Q3 is nummer 10-11 van de 13 en dat is 67
De kwartielafstand is dan   67 - 36,5 = 30,5

de deviaties zijn:  
14.154, 14.154, 14.154, 11.154, 7.154, 7.154, 7.154, 7.154, 6.846, 17.846, 17.846, 18,846, 20.846
Het gemiddelde daarvan is  12,65
       
2.
meting [5, 17〉 [17, 29〉 [29, 41〉 [41, 53〉 [53, 65〉 [65, 77〉 [77, 89〉
frequentie 12 35 58 123 88 73 87
  De spreidingsbreedte (grootste min kleinste) is 89 - 5 = 84

De klassenmiddens zijn  11, 23, 35, 47, 59, 71, 83
Het gemiddelde is  
(12 • 11 + 35 • 23 + 58 • 35 + 123 • 47 + 88 • 59 + 73 • 71  + 22 • 83)/(12 + 35 + 58 + 123 + 88 + 73 + 87) = 26344/476 = 55,34
gemiddelde deviatie.
De deviaties zijn  44.34, 32.34, 20.34, 8.34, 3.66, 15.66, 27.66
het gemiddelde daarvan is  
(12 • 44.34 + 35 • 32.34 + 58 • 20.34 + 123 • 8.34 + 88 • 3.66 + 73 • 15.66 + 22 • 27.66)/476 = 7741,2/476 =16,26
kwartielafstand.
Er zijn 476 getallen dus de middelste is nr. 238/239 en het eerste kwartiel is dan nr. 119/120 en het derde kwartiel is nr. 357/358
Het eerste kwartiel zit in de klasse, 29-41 en is nummer 72,5 daaruit.  dat is op 25,5/58 = 0,44ste deel dus dat is 
29 + 0,44 * 12 = 34,3
Het derde kwartiel zit in de klasse 53-67 en is nummer 80,5 daaruit. Dat is op  80,5/88 =0,91ste deel dus dat is  53 + 0,91 • 12 = 63,9
De kwartielafstand is dan 63,9 - 34,2 = 29,6
       
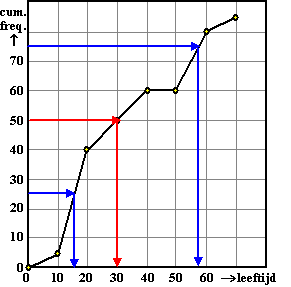
3. zie de figuur hiernaast.

de mediaan zit bij 50% (rode lijnen) en is ongeveer 30

de 1e en 3e kwartielen zitten bij 25% en 75% (blauwe lijnen) en  zijn ongeveer 15 en 58. Dus de kwartielafstand is 58 - 15 = 43.

de modus vind je bij het steilste gedeelte, en dat is de klassen 10-20
       
4. de mediaan is 12, dus het middelste getal is 12.
dat geeft de getallen    •  • 12  •  •   en die wil je graag zo dicht mogelijk bij elkaar hebben liggen.
de 4 getallen om de 12 heen moeten samen 38 zijn  (gemiddelde 10, dus samen 50, dus de vier ontbrekenden zijn samen 38).
Rechts van 12 kan 12 - 12 staan, dus dat geeft   • • 12 12 12
De 2 ontbrekenden zijn samen 14, dus dat is 7 7  (zo dicht mogelijk bij 12).
Dat geeft de serie  7  7  12  12  12
De spreidingsbreedte is  12 - 7 = 5
       
5. a. Het totaal van de vijf waarnemingen is 53.  x1 + x2 = 23 dus de gezochte drie zijn samen 30.
Het verschil tussen de grootste en kleinste van de vijf moet 11 zijn.
Er zijn meerdere goede oplossingen, bijv: 14 , 13 , 3  of  16 , 9 , 5
       
  b. We zoeken vijf getallen waarvan de spreiding groter is dan 20, maar waarvan het gemiddelde wel tussen de 5 en 15 ligt. Er zijn vele goede oplossingen.
Bijv.  0,0,0,0,30  met bijbehorende gewichten  500, 500, 500, 500, 530.
       
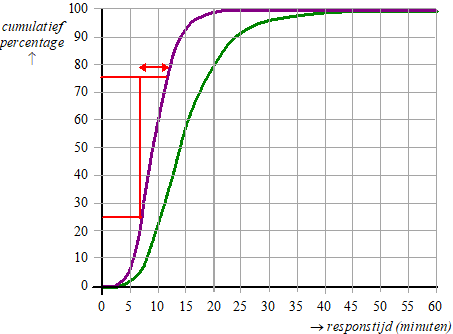
6. Je moet de linker polygoon hebben want daar zijn de meeste ritten kort.

25%:  7
75%:  11,5

afstand is dus  11,5 - 7 = 4,5
(zie de rode pijltes)
       

© h.hofstede (h.hofstede@hogeland.nl)