© h.hofstede (h.hofstede@hogeland.nl)

       
1.
  B niet-B totaal
A a b  
niet-A c d  
totaal      
       
  Van de  a + c gevallen met eigenschap B zijn er a met eigenschap A, dus P(A \ B) = a/(a + c)
P(A) = (a + b)/(a + b + c + d)
Als die gelijk zijn dan moet dus gelden  a/(a + c) = (a + b)/(a + b + c + d)  ofwel  a(a + b + c + d) = (a + c)(a + b)

Van de a + b gevallen met eigenschap A zijn er a met eigenschap B, dus  P(B \ A) = a/(a + b)
P(B) = (a + c)/(a + b + c + d)
Als die gelijk zijn dan moet dus gelden  a/(a + b) = (a + c)/(a + b + c + d)  ofwel  a(a + b + c + d) = (a + c)(a + b)  

Dat zijn dus inderdaad dezelfde twee voorwaarden.
       
2. P(spieken \ meisje) = 1280/1680 = 0,7619
P(spieken) = 2680/3500 = 0,7657
Dat is niet gelijk, dus de eigenschappen zijn AFHANKELIJK.
       
3. a.
  prijs niet-prijs totaal
geel 0 5000 5000
blauw 2250 750 3000
oranje 1250 750 2000
totaal 3500 6500 10000
 
       
  b. P(blauw \ prijs) = 2250/3500 = 0,6429
P(blauw) = 3000/10000 = 0,3
Dat is niet gelijk dus het is AFHANKELIJK		  
       
  c. P(oranje \ niet-prijs) = 750/6500 = 0,1154
P(oranje) = 2000/10000 = 0,2
Dat is niet gelijk dus het is AFHANKELIJK		  
       
4. P(even \ vijfvoud) = 4/8  (want van de 8 vijfvouden 5, 10, 15, 20, 25, 30, 35, 40 zijn er 4 even)
P(even) = 1/2
Dat is gelijk, dus de gebeurtenissen A en B zijn ONAFHANKELIJK
       
5. a.
  inkomen hoger dan 40000 inkomen lager dan 40000  
wel drugs x   315
geen drugs     2485
  480 2320 2800
       
    Dit zijn de gegevens uit de tekst.
Omdat de eigenschappen onafhankelijk zijn moet gelden   x/480 = 315/2800
Dat geeft x = 54 en daarmee is de tabel verder in te vullen:
       
   
  inkomen hoger dan 40000 inkomen lager dan 40000  
wel drugs 54 261 315
geen drugs 426 2059 2485
  480 2320 2800
       
    P(lager dan 40000 en geen drugs) = 2059/2800 = 0,7354
       
  b. Van de 480 volwassenen met een inkomen hoger dan 40000 gebruiken er 54 drugs.
De kans is dus 54/480 = 0,1125
       
6.
  PvdA VVD overig  
komt wel opdagen 3800 3220 2425 9445
komt niet opdagen 200 280 75 555
  4000 3500 2500 10000
       
  a. 9445 van de 10000 komen opdagen dus dat is  94,45%  
       
  b. Van de 555 niet-opdagers zijn er 280 VVDers. De kans is dus  280/555 = 0,5045
       
  c. P(komt opdagen \ PvdA) = 3800/4000 = 0,95
P(komt opdagen) = 9445/10000 = 0,9445
Dat is niet gelijk, dus de gebeurtenissen zijn AFHANKELIJK
       
  d. Stel dat een deel  x van de andere partijen niet komt opdagen.
Dan komt in totaal van de 10000 mensen er  200 + 280 + 2500x = 480 + 2500x niet opdagen
Het percentage niet-opdagen bij de overige partijen moet gelijk zijn aan het percentage niet-opdagers in het totaal.
Dus moet gelden:  10000x = 480 + 2500x
7500x = 480
x = 480/7500 = 0,064
Dus 6,4% van de overige partijen zou niet moeten komen opdagen om het onafhankelijk te maken. 
       
7. Vanwege de laatste twee voorwaarden kun je de volgende tabel maken:
       
 
  A B C  
D        
E        
         
       
  Vul de andere voorwaarden in bij 100 gevallen:
       
 
  A B C  
D x y   70
E       30
  10 40 50 100
       
  omdat A en D onafhankelijk zijn geldt  P(D \ A) = P(D)  dus   x/10 = 0,7  dus x = 7
omdat B en D onafhankelijk zijn geldt  P(D \ B) = P(D)  dus   y/40 = 0,7  dus  y = 28
Dat geeft de volgende tabel:
       
 
  A B C  
D 7 28 35 70
E 3 12 15 30
  10 40 50 100
       
  P(C \ E) = 15/30 = 0,5
P(C) = 0,5
Dat is gelijk dus C en E zijn ONAFHANKELIJK
       
8.
  Kees Henk Gert  
is te laat 20 80 150 250
is op tijd 980 1920 2850 5750
  1000 2000 3000 6000
       
  a. P(te laat \ Henk) = 0,04
P(te laat) = 250/6000 = 0,042
Dat is niet gelijk dus de gebeurtenissen zijn AFHANKELIJK
       
  b. 5750/6000 = 0,9583
       
  c. van de 250 keer te laat was het 150 keer Gert.
De kans is dus 150/250 = 0,6
       
9. a. De helft zegt JA vanwege het muntstuk.
Van de andere helft zegt nog eens 12% ook JA omdat ze spieken. Dat is 0,5 • 0,12 = 0,06
Samen geeft dat  0,5 + 0,06 = 0,56
       
  b. 44 hebben JA geantwoord vanwege het muntstuk.
Van de andere 44 hebben er nog eens 52 - 44 = 8  ook JA geantwoord.
Van die andere 44 zullen er dus ook naar verwachting 8 gespiekt hebben.
Er zullen naar verwachting dus 16 leerlingen gespiekt hebben.
       
  c. binomiaal verdeeld.
n = 20
p = 0,25
P(X = 8) = binompdf(20, 0.25, 8) = 0,0609
       
  d.
       
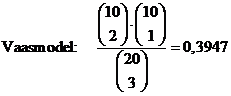  e. P(meisje \ spiekt nooit) = 10/24 = 0,4167
P(meisje) =  20/48 = 0,4167
Dat is gelijk dus de gebeurtenissen zijn ONAFHANKELIJK.
       
  f. :)  
       
10. a. 2 dozen leeg:   500 en 050 en 005 dat zijn 3 mogelijkheden
D1 leeg:     041 en 032 en 023 en 014  dat zijn 4 mogelijkheden
D2 leeg en D3 leeg geven zo ook 4 mogelijkheden
geen dozen leeg:  311, 131, 113, 221, 212, 122  en dat zijn 6 mogelijkheden
Samen geeft dat 3 + 4 + 4 + 4 + 6 = 21 mogelijkheden
Dus er zijn nog 20 andere mogelijkheden.   
       
  b. van de 21 mogelijkheden hierboven geven de volgende aantallen in D1:
X2 = 0:  0 balletjes in D2:  500, 005, 401, 104, 302, 203 dat zijn 6 mogelijkheden.

X1 = 2:  2 balletjes in D1:  230, 203, 221, 212 dat zijn 4 mogelijkheden dus kans 4/21
X1 = 3:  3 balletjes in D1:  311, 320, 302  dat zijn 3 mogelijkheden dus kans 3/21
(X1 = 2  ∨  X1 = 3)  heeft dus kans  4/21 + 3/21 = 7/21 = 1/3

(X1 = 2  X1 = 3) \ X2 = 0  zijn de mogelijkheden:  203, 302 dat zijn twee mogelijkheden van de 6 manieren waarbij X2 = 0, dus de kans is 2/6 = 1/3
De kansen zijn gelijk dus de gebeurtenissen zijn ONAFHANKELIJK.
       
  c. Alle mogelijkheden:
500, 050, 005, 041, 032, 023, 014, 401, 104, 302, 203, 410, 140, 230, 320, 311, 131, 113, 221, 212, 122
Y2: het aantal dozen dat precies twee balletje bevat is achtereenvolgens:
0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1
12 keer 0 en 9 keer 1.

Dat geeft de kansverdeling:

   
Y2 P
0
1		 12/21
9/21
    Y1 = 1 (1 doos met 1 balletje) geeft de mogelijkheden  041, 014, 104, 401, 140, 410, 221, 212, 122.
Y2 = 0 (geen dozen met 2 balletjes) zijn daarvan de mogelijkheden  041, 014, 104, 401, 140, 410
Dat zijn er  6 van de 9 dus de kans is 6/9 = 2/3
       

© h.hofstede (h.hofstede@hogeland.nl)