|
|||||
| 1. | n is onbekend
= X marktkoopman 1: p = 0,80 (succes is een goede appel) P(k ≥ 20) = 1 - P(k ≤ 19) = 1 - binomcdf(X, 0.80, 19) Y1 = 1 - binomcdf(X, 0.80, 19) Kijk bij TABLE wanneer dat voor het eerst groter dan 0,99 is. Dat geeft X = 32 (kans 0,99395) Je moet dus 32 appels kopen en dat kost 32 0,16 = 5,12 marktkoopman 2: p = 0,85 (succes is een goede appel) P(k ≥ 20) = 1 - P(k ≤ 19) = 1 - binomcdf(X, 0.85, 19) Y1 = 1 - binomcdf(X, 0.85, 19) Kijk bij TABLE wanneer dat voor het eerst groter dan 0,99 is. Dat geeft X = 29 (kans 0,99706) Je moet dus 29 appels kopen en dat kost 29 0,18 = 5,22 Marktkoopman 1 is het goedkoopst, en het gaat 5,12 kosten. |
||||
| 2. | a. | n = 306 p = 0,50 (kans op winst thuisspelende ploeg) P(X < 170) = P(X ≤ 169) = binomcdf(306, 0.50, 169) = 0,9705 |
|||
| b. | n = 306 p = 0,20 (kans op winst uitspelende ploeg) P(X ≥ 80) = 1 - P(X ≤ 79) = 1 - binomcdf(306, 0.20, 79) = 0,0,0055 |
||||
| c. | In 306 wedstrijden
kunnen maximaal 306 3 = 918 punten gehaald worden (als er geen
gelijkspellen zijn) Elk gelijkspel zorgt voor 1 punt minder (1-1 in plaats van 3-0) 846 punten betekent dus 72 gelijkspellen. n = 306 p = 0,30 (kans op gelijkspel) P(X = 72) = binompdf(306, 0.30, 72) = 0,0022 |
||||
| 3. | a. | P(2e raak)
= P(1e raak en 2e raak) + P(1e mis en 2e
raak) = 0,70 0,80 + 0,30 0,60 = 0,74 |
|||
| b. | n = 100 p = 0,74 (vraag a) P(X ≥ 80) = 1 - P(X ≤ 79) = 1 - binomcdf(100, 0.74, 79) = 0,1027 |
||||
| 4. | a. | n = 400 p = 0,60 P(X > 250) = 1 - P(X ≤ 250) = 1 - binomcdf(400, 0.60, 250) = 0,1418 |
|||
| b. | n = ? p = 0,60 P(X > 200) = 1 - P(X ≤ 200) = 1 - binomcdf(?, 0.60, 200) < 0,05 Y1 = 1 - binomcdf(X, 0.60, 200) Kijk bij TABLE wanneer dat kleiner is van 0,05 Dat is bij X = 0 tot en met 310 De winkelier kan maximaal 310 bonnen uitdelen |
||||
| 5. | a | P(wel, wel) = 1/32 1/32 = 0,00097656 dus dat is ongeveer 0,001 | |||
| b. | n = 500 p = 0,001 (vraag a) P(X = 4) = binompdf(500, 0.001, 4) = 0,0016 |
||||
| c. | n = 500 p = 0,001 (vraag a) P(X ≥ 4) = 1 - P(X ≤ 3) = 1 - binomcdf(500, 0.001, 3) = 0,0,0017 |
||||
| d. | n = 500 p = ? P(X = 4) = binompdf(500, ?, 4) = 0,002 Y1 = binompdf(500, X, 4) Y2 = 0,002 intersect geeft X = 0,0266 of X = 0,00107 en dat is p2 Dus p = √0,0266 = 0,163 of p = √0,00107 = 0,033 Die eerste is wel ERG groot, dus waarschijnlijk zal de tweede de gezochte kans zijn. |
||||
| 6. | a. | n = 20 p = 0,08 P(X = 3) = binompdf(20, 0.08, 3) = 0,1414 |
|||
| b. | n = 50 p = 0,02 P(X ≥ 5) = 1 - P(X ≤ 4) = 1 - binomcdf(50, 0.02, 4) = 0,0032 |
||||
| c. | Als er F fietsers
zijn, dan zijn er 540 - F auto's geweest. 0,08F + 0,02(540 - F) = 24 0,08F + 10,8 - 0,02F = 24 0,06F = 13,2 F = 220 Dat zijn dus 220 fietsers en 320 auto's geweest. |
||||
| 7. | a. | 0,8745 = 0,0019 | |||
| b. | n = 45 p = 0,13 (kans dat Giri niet wint) P(X ≥ 10) = 1 - P(X ≤ 9) = 1 - binomcdf(45, 0.13, 9) = 0,0602 |
||||
| c. | Dat is 5 verlies, 30
winst en 10 remise. 0,035 0,8730 0,1010 (45 nCr 5) (40 nCr 30) = 0,000039 |
||||
| 8. | P(spijbelen) = P(6) +
P(5 en dan 6) = 1/6
+ 1/6
1/6
= 7/36 P(opdagen) = 1 - 7/36 = 29/36 n = 23 p = 29/36 P(X < 18) = P(X ≤ 17) = binomcdf(23, 29/36, 17) = 0,2813 |
||||
| 9. | Er zijn drie manieren
om te ontsnappen: I: via de onderste rij: dan moet je direct 7 keer Oost kiezen. kans is (4/6)7 = 0,0585 II: via de één na onderste rij. Dan moet je na 7 stappen 6 keer Oost en één keer Noord hebben gekozen, en de achtste stap moet Oost zijn. Kans: binompdf(7, 4/6, 6) 4/6 = 0,1366 III: via de tweede rij van onderen: Dan moet je na 8 stappen 2 Noord en 6 Oost hebben gekozen, en de negende stap Oost nemen. Kans: binompdf(8, 4/6, 6) 4/6 = 0,1821 Samen geeft dat kans 0,0585 + 0,1366 + 0,1821 = 0,3772 |
||||
| 10. | 11 mensen moeten een
muntstuk opgooien, dus n = 11 De kans dat iemand hem schuldig vindt is dan 0,5 De verdachte wordt veroordeeld als minstens 11 mensen hem schuldig vinden, dus van de muntstukgooiers moeten minstens 6 hem schuldig vinden P(X ≥ 6) = 1 - P(X ≤ 5) = 1 - binomcdf(11, 0.5, 5) = 0,5 |
||||
| 11. | n = aantal
mensen = ? p = kans op jarig op 19 maart = 1/36 P(X ≥ 3) = 1 - P(X ≤ 2) = 1 - binomcdf(X, 1/36, 2) Y1 = 1 - binomcdf(X, 1/365, 2) Kijk bij TABLE wanneer dat voor het eerst groter dan 50% is. Dat is vanaf X = 976 De groep moet dus minstens 976 mensen zijn. |
||||
| 12. | a. | n = 19 p = 0,80 (kans dat iemand WEL komt opdagen) Er is overbezetting als er meer dan 16 mensen komen opdagen. P(X > 16) = 1 - P(X ≤ 16) = 1 - binomcdf(19, 0.80, 16) = 0,2369 |
|||
| b. | n = ? p = 0,80 (kans dat iemand WEL komt opdagen) Er is overbezetting als er meer dan 16 mensen komen opdagen. P(k > 16) = 1 - P(k ≤ 16) = 1 - binomcdf(X, 0.80, 16) Y1 = 1 - binomcdf(X, 0.80, 16) Kijm bij TABLE voor welke waarden dat kleiner dan 0,1 is. Dat is bij n kleiner dan 19. Het aantal huurders is maximaal 18. |
||||
| 13. | a. | 0,3 0,3 0,3 0,3 0,3 0,7 0,7 0,7 0,7 0,7 = 0,0004 | |||
| b. | binomiaal verdeeld
met n = 40, p = 0,3 P(X > 12) = 1 - P(X ≤ 12) = 1 - binomcdf(40, 0.3, 12) = 0,423 |
||||
| 14. | a. | binomiaal
met n = 50 en p = 0,9 P(X ≥ 45) = 1 - P(X ≤ 44) = 1 - binomcdf(50 , 0.9 , 44) = 0,62 |
|||
| b. | Voor
één bedrijf is de kans na 5 jaar te overleven 0,955 =
0,77378 n = 144, p = 0,77378 P(X ≥ 100) = 1 - P(X ≤ 99) = 1 - binomcdf(144, 0,77378 , 99) = 0,99 |
||||
| 15. | n = 5 p = 0,75 P(X ≥ 5) = 1 - P(X ≤ 4) = 1 - binomcdf(10, 0.75, 4) » 0,98 |
||||
| 16. | a. | P(geen
prijs) = 0,95 0,80 = 0,76 Dus P(minstens één prijs) = 1 - 0,76 = 0,24 |
|||
| b. | Binomiaal
met n = 20, p = 0,24 P(X ≥ 8) = 1 - P(X ≤ 7) = 1 - binomcdf(20, 0.24 , 7) = 0,083 |
||||
| 17. | a. | binomiaal verdeeld
met n = 154 en p = 0,05 P(X ≤ 2) = binomcdf(154, 0.05, 2) = 0,015 |
|||
| b. | binomcdf(154, X, 2)
= 0,05 Y1 = binomcdf(154, X, 2) en Y2 = 0,05 window bijv. Xmin = 0, Xmax = 1, Ymin = 0, Ymax = 0,1 intersect geeft p = 0,04 |
||||
| 18. | a. | het aantal
schadegevallen is binomiaal verdeeld met n = 800 en p
= 0,01 P(6) = binompdf(800, .01, 6) = 0,1223 |
|||
| b. | P(X ≥ 20) = 1 - P(X ≤ 19) = 1 - binomcdf(800, 0.01, 19) = 0,0002317 | ||||
| 19. | a. | Er zijn twee
mogelijkheden: F, NF, F, NF, F, NF, F, NF, F, NF en NF, F, NF, F, NF, F, NF, F, NF, F De kans op beiden is gelijk, en die is 5/10 4/9 4/8 4/7 3/6 3/5 2/4 2/3 1/2 1 = 1/252 De totale kans is daarom 2 1/252 = 1/126 ≈ 0,008 (of: er zijn 10 nCr 5 = 252 mogelijkheden, waarvan 2 gunstig, dus de kans is 2/252) |
|||
| b. | Voor één persoon
is die kans 0,2. Het aantal proefpersonen dat de eerste dag tablet 1 of 2 kiest is binomiaal verdeeld. Het aantal experimenten is n = 18. De kans op succes (1 of 2 kiezen) per keer is 0,2 Het gaat om 6 of meer successen, dus P(X ³ 6) = 1 - P(X ≤ 5) = 1 - binomcdf(18, 0.2, 5) = 0,133 |
||||
| 20. | a. | het
aantal ritten is binomiaal verdeeld met n = 40 en p = 0,5. P(X ≥ 26) = 1 - P(X ≤ 25) = 1 - binomcdf(40, .5, 25) = 0,0403 |
|||
| b. | precies 26 geeft
kans binompdf(40, p, 26) voer in de GR in: Y1 = binompdf(40, p, 26) kijk bij TABLE wanneer dat maximaal is. (Tblset - Tblstart 0,5 en ΔTbl 0,01 geeft de tabel hiernaast) Het maximum zit inderdaad bij p = 0,65 |
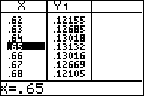 |
|||
| 21. | a. | Voor elk antwoord zijn er steeds 4 mogelijkheden. Samen geeft dat 4 4 4 ..... = 410 = 1048576 mogelijkheden. |
|||
| b. | De kans op een goed antwoord is elke keer
1/3. Dat is dus binomiaal verdeeld. n = 10 p = 1/3 P(X ≤ 5) = binomcdf(10, 1/3, 5) = 0,9234 |
||||
| 22. | a. | Bij
één dag is de kans dat ze op tijd is 0,866 Voor vijf dagen is dan de kans 0,8665 = 0,487 en dat is inderdaad kleiner dan 0,5 |
|||
| b. | In 19
weken zijn er 19 5 = 95 schooldagen. n = 95 p = 0,134 (de kans dat de trein te laat komt is 1 - 0,866) P(X ≥ 9) = 1 - P(X ≤ 8) = 1 - binomcdf(95, 0.134, 8) = 0,9038 |
||||
| c. | P(0
keer officieel te laat) = P(0 of 1 keer echt te laat) binomcdf(5, 0.134, 1) = 0,8638.... en dat is afgerond 0,864 P(1 keer officieel te laat) = P(2 keer echt te laat) binompdf(5, 0.134, 2) = 0,1166.... en dat is afgerond 0,117 |
||||
| 23. | a. | Als er
meer dan 65 over zijn, dan moeten meer dan 17 van de gokkers het goed
hebben. Dit is voor de gokkers een binomiaal experiment met n = 52, p = 1/3 P(X > 17) = 1 - P(X ≤ 17) = 1 - binomcdf(52, 1/3, 17) = 0,4739 |
|||
| b. | Als X
spelers gokken, zullen daarvan 1/3X het goed hebben De andere 70-X mensen wisten het dus zeker. Dan zijn er uiteindelijk 70 - X + 1/3X mensen over zijn. 70 - X + 1/3X = 54 ⇒ 2/3X = 16 ⇒ X = 24. Er hebben naar verwachting 24 mensen gegokt. |
||||
| 24. | a. | de
helft is 254 mannen. Dit is binomiaal verdeeld met n = 508 en p = 0,52 P(X = 254) = binompdf(508, 0.52, 254) = 0,0236 |
|||
| b. | Dit is
binomiaal verdeeld met n = 219 en p = 0,71. P(meer dan 150 maar minder dan 165) = P(150 < X < 165) = P(X ≤ 164) - P(X ≤ 150) = binomcdf(219, 0.71, 164) - binomcdf(219, 0.71, 150) = 0,9117 - 0,2273 = 0,684 |
||||
| c. | P(X ≥ 50) = 1 - P(X ≤
49) = 1 - binomcdf(508, p, 49) = 0,816 Y1 = 1 - binomcdf(508, X, 49) Y2 = 0,816 intersect geeft dan een kans van p = 0,11 |
||||
| d. | P(voldoende vrouwen in leven) = P(minstens 50 vrouwen in leven) = P(X > 50) = 1 - P(X ≤ 49) = 1 - binomcdf(219, 0.26, 49) = 0,8750 De kans dat er voldoende mannen in leven zijn is 0,816 De kans dat beiden voorkomt is dan 0,816 0,8750 = 0,714 |
||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||