|
|||||
| 1. | Vaas I: x
rode en 12 - x zwarte Vaas II: x rode en 20 - x zwarte P(rood en zwart) = P(RZ) + P(ZR) = x/12 (20-x)/20 + (12 - x)/12 x/20 = (x(20 - x) + (12 - x)x)/240 = 1/240 (20x - x2 + 12x - x2 ) = 1/240 (32x - 2x2 ) Dat stuk tussen haakjes is een bergparabool en die is maximaal bij x = -b/2a = -32/-4 = 8 Dan is P = 1/240 128 = 8/15 |
||||
| 2. | Stel x rode en
10 - x zwarte knikkers. P(rood en zwart) = P(RZ) + P(ZR) = x/30 (30 - x)/29 + (30 - x)/30 x/29 = (x(30 - x) + (30 - x)x)/870 = 1/870 (30x - x2 + 30x - x2) = 1/870 (60x - 2x2 ) = 0,4046 60x - 2x2 = 352 2x2 - 60x + 352 = 0 ABC formule geeft x = 22 of x = 8 |
||||
| 3. | a. | Stel dat er n
vrienden zijn Er zijn dan n · (n - 1) · .... · 1 = n! manieren om een rijtje te gokken. Daarvan is er één goede, dus de kans is 1/n! 1/n! = 0,00139 dus n! = 1/0,00139 = 719 Y1 = X! en dan TABLE geeft 719 bij n = 6 (720) |
|||
| b. | Op dezelfde manier:
n! = 0,000000000001 geeft n! = 1/0,000000000001
= 1.000.000.000.000 TABLE levert n = 15 |
||||
| 4. | Stel dat de klas bestaat uit x meisjes en 28-x jongens. | ||||
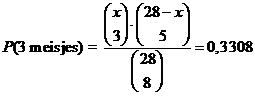 |
|||||
| De formule invoeren bij Y1 en dan in TABLE kijken geeft x = 10 | |||||
| 5. | Stel 7 gevlekte muizen en n zwarten. | ||||
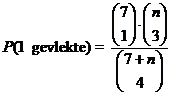 |
|||||
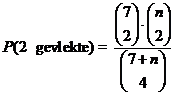 |
|||||
| Invoeren bij Y1 en Y2
en kijken wanneer ze gelijk zijn geeft n = 11 Er zitten dus 7 + 11 = 18 muizen in de bak. |
|||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||