|
|||||
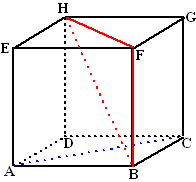
| 1. | AC staat loodrecht op
DB want dat zijn de diagonalen van een vierkant. Dus AC staat ook loodrecht op HF AC staat loodrecht op CG want dat zijn de zijden van een rechthoek Dus AC staat ook loodrecht op BF AC staat loodrecht op HF en op BF dus op vlak HFB. |
 |
|||
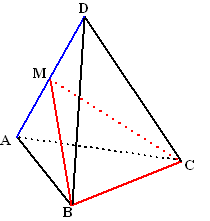
| 2. | AD staat loodrecht op
CM want CM is de hoogtelijn van de gelijkzijdige driehoek ACD AD staat loodrecht op BM want BM is de hoogtelijn van de gelijkzijdige driehoek ABD AD staat loodrecht op CM en op BM dus op vlak BMC |
 |
|||
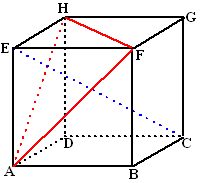
| 3. | Verplaats AF naar MN
met M het midden van AD en N het midden van FG. Dan snijden AF en EC elkaar in het midden S van de kubus. ME = MC = CN = NE (allemaal schuine zijden van dezelfde rechthoekige driehoeken) Dus MCNE is een ruit, dus staan de diagonalen EC en MN loodrecht op elkaar. Dus staan ook EC en AF loodrecht op elkaar. Op dezelfde manier kun je HF verplaatsen naar PQ (P midden van HD en Q midden van BF. Ook dan krijg je een ruit PEQC dus staan ook EC en HF loodrecht op elkaar. EC staat loodrecht op AF en op HF dus op vlak AHF |
 |
|||
| 4. |
|
||||
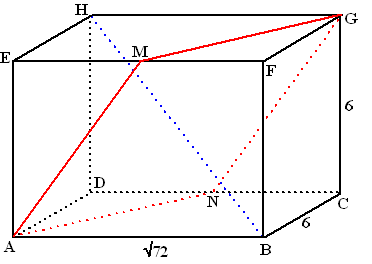
| a. | BG2 = 62
+ 62 = 72 dus BG = √72 Dus ABGH is een vierkant en daarvan staan de diagonalen loodrecht op elkaar. Dus staan AG en HB loodrecht op elkaar. |
||||
| b. | HM en MB en BN en NH
zijn allemaal de schuine zijde van een rechthoekige driehoek met
rechthoekszijden 6 en 1/2√72. Dus zijn ze allemaal even lang, dus is HMBN een ruit. Dan staan de diagonalen HB en MN loodrecht op elkaar. HB staat loodrecht op AG (vraag a) en op MN, dus op vlak AMGN |
||||
| 5. |
|
||||
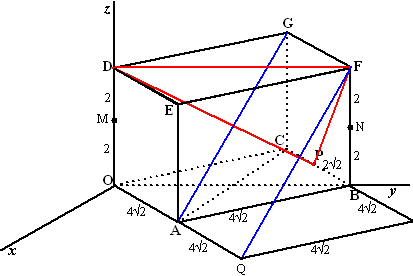
| Verplaats DF naar MN
met M het midden van OD en N het midden van FB. Dan zijn MA en AN en NG en GM allemaal schuine zijden van rechthoekige driehoeken waarvan de rechthoekszijden 4√2 en 2 zijn. Dus zijn ze alle vier even lang. Dus is MANG een ruit en staan de diagonalen AG en MN loodrecht op elkaar. Dus staat AG loodrecht op DF. Verplaats GA naar FQ (zie de figuur) FQ2 = 42 + (4√2)2 + (4√2)2 = 80 PQ2 = (6√2)2 + (4√2)2 = 104 FP2 = 42 + (2√2)2 = 24 PQ2 = FQ2 + FP2 (want 104 = 80 + 24) Dus in driehoek FPQ geldt Pythagoras, dus is de driehoek rechthoekig. Dus staat QF loodrecht op FP. Dus staat AG loodrecht op FP AG staat loodrecht op FD en op DF dus op vlak DFP. |
|||||
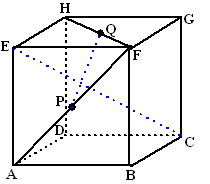
| 6. | EC staat loodrecht op
vlak AHF (opgave 3) dus op alle lijnen uit AHF dus ook op PQ. BH staat loodrecht op vlak AFC (zie opgave 3) dus op alle lijnen uit AHC dus ook op PC. |
 |
|||
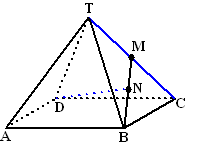
| 7. | TC staat loodrecht op
DM (hoogtelijn gelijkzijdige driehoek) TC staat loodrecht op BM (hoogtelijn gelijkzijdige driehoek) Dus TC staat loodrecht op vlak DMB, dus op alle lijnen uit dat vlak. Dus ook op DN. |
 |
|||
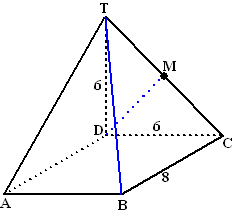
| 8. | DM staat loodrecht op
TC (diagonalen van een vierkant) AD staat loodrecht op DT en op DC dus op heel vlak TDC, dus ook op DM Dan staat BC ook loodrecht op DM want die is evenwijdig aan AD. DM staat dus loodrecht op BC en op Tc dus op heel vlak TBC Dus loodrecht op alle lijnen uit TBC, dus ook op TB |
 |
|||
| 9. |
|
||||
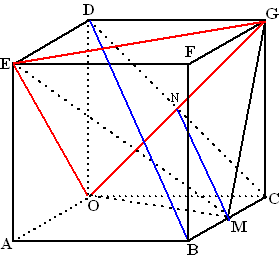
| Zie het viervlak als
een piramide met grondvlak EOG en top M. BD staat loodrecht op EOG (opgave 3), dus de lijn van M evenwijdig aan BG ook. Die snijdt het grondvlak in punt N (want BD en MN liggen in vlak BCDE) Dus de hoogte van de piramide is MN. OM2 = 42 + 22 = 20 dus OM = √20 en ook MG = √20 OG2 = 42 + 42 = 32 dus OG = √32 OMG is gelijkbenig met hoogtelijn MN, dus MN2 = MG2 - NG2 = 20 - (1/2√32)2 = 20 - 8 = 12 MN = √12 OGE is gelijkzijdig met zijden √32, EN2 = EO2 - ON2 = (√32)2 - (1/2√32)2 = 24 dus EN = √24 Het grondvlak OGE heeft oppervlakte 1/2 • √32 • √24 = 1/2√768 De inhoud van het viervlak is 1/3 • 1/2√768 • √12 = 1/6√9216 = 1/6 • 96 = 16 |
|||||
| 10. |
|
||||
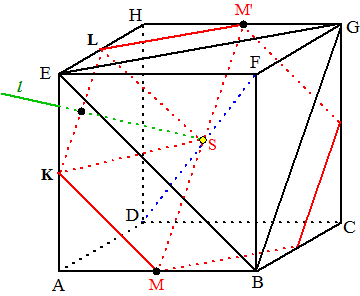
| a. | EBG staat loodrecht
op DF, dus de rode zeshoek ook. Ui symmetrie kin je zien dat M' tegenover M op de zeshoek ligt. Het draaui[punt is S. |
||||
| b. | Trek de lijn van S naar het midden van KL, die maakt 90º met SM (nl. 60 + 30). Dus M'' ligt op lijn l (net buiten de kubus) | ||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||