|
|||||
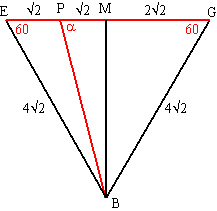
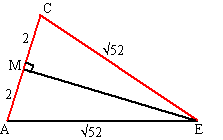
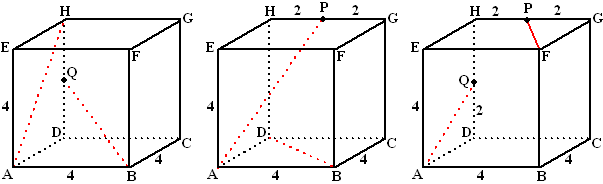
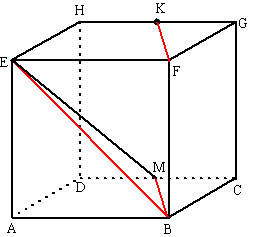
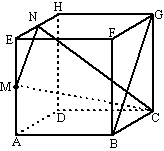
| 1. | a. | Driehoek EBG is gelijkzijdig met
zijden 4√2. BM2 + EM2 = EB2 BM2 = (4√2)2 - (2√2)2 = 32 - 8 = 24 BM = √24 tanα = √24/√2 = √12 α = tan-1 √12 = 73,9º |
|
||
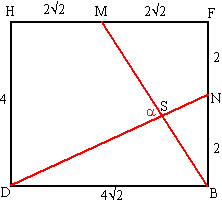
| b. | tan(NDB) = 2/4√2
∠NDB = tan-1 (2/4√2) = 19,47º tan(MBF) = 2√2/4 ∠MBF = tan-1(2√2/4) = 35,26º dan is ∠DBM = 90º - 35,26º = 54,74º dan is ∠DSB = 180º - 54,74º - 19,47º = 105.79º α = 180º - 105,79º = 74,2º |
|
|||
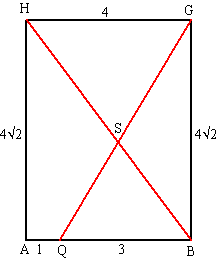
| c. | tan(BQG) = 4√2/3 ∠BQG = tan-1(4√2/3) = 62,06º tan(HBG) = 4/4√2 ∠HBG = tan-1(4/4√2) = 35,26º dan is ∠QBS = 90º - 35,26º = 54,74º dan is ∠QSB = 180º - 54,74º - 62,06º = 63,2º |
|
|||
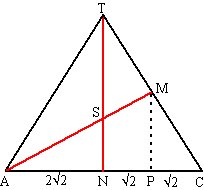
| d. | M is het midden van TC, dus is MP
= 1/2TN
= 2 tan(PAM) = MP/PA = 2/3√2 ∠PAM = tan-1(2/3√2) = 25,24º ∠ASN = 180º - 90º - 25,24º = 64,8º |
|
|||
| e. | EC = AE =
√52 (Pythagoras) Dus driehoek ACE is gelijkbenig, en MC = MA = 2 cos(MCE) = MC/CE = 2/√52 ∠MCE = cos-1(2/√52) = 73,9º |
|
|||
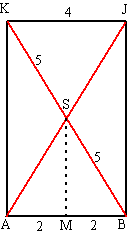
| f. | Als K' het punt onder K is, dan
is BK' = 8 (2 zijden van gelijkzijdige driehoekjes van 4) Dan is BK2 = 82 + 62 = 100 dus BK = 10 sin(MSB) = MB/SB = 2/5 ∠MSB = sin-1(2/5) = 23,58º ∠ASB = 2 • 23,58º = 47,2º |
|
|||
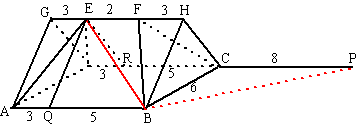
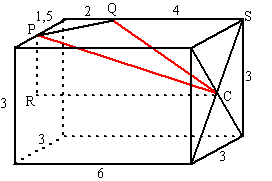
| 2. | Noem het midden van
het linkerzijvlak R. CP2 = CR2 + PR2 = 62 + 1,52 = 38,25 CP = √38,25 CS2 = 1,52 + 1,52 = 4,5 CQ2 = CS2 + QS2 = 4,5 + 42 = 20,5 CQ = √20,5 PQ2 = 22 + 1,52 = 6,25 dus PQ = √6,25 = 2,5 |
 |
|||
| CPQ is een driehoek
met zijden √38,25 en
√20,5 en 2,5 cosinusregel: 2,52 = 38,25 + 20,5 - 2 • √38,25 • √20,5 • cos(QCP) cosQCP = 0,9374 ∠QCP = cos-10,9374 = 20,4º |
|||||
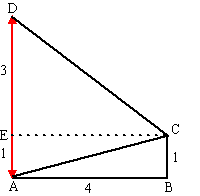
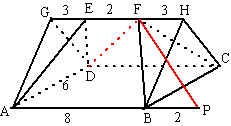
| 3. | a. | tan(ECD) = 3/4
dus ∠ECD = tan-1(3/4)
= 36,87º tan(ECA) = 1/4 dus ∠ECA = tan-1(1/4) = 14,04º dan is ∠ACD = 36,87º + 14,04º = 50,9º |
|
||
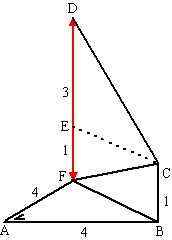
| b. | BF2 = 42 +
42 = 32 dus BF = √32
= CE tan(FCE) = 1/√32 dus ∠FCE = tan-1 (1/√32) = 10,02º tan(ECD) = 3/√32 dus ∠ECD= tan-1(3/√32) = 27,94º dan is ∠FCD = 10,02º + 27,94º ≈ 38,0º |
|
|||
| c. | Herhaal de berekening
van vraag b) maar nu met AF = x BF2 = 42 + x2 = 16 + x2 dus BF = √(16 + x2) tan(FCE) = 1/√(16 + x2) dus ∠FCE = tan-1 (1/√(16 + x2) ) tan(ECD) = 3/√(16 + x2) dus ∠ECD = tan-1(3/√(16 + x2) ) ∠FCD = tan-1 (1/√(16 + x2) ) + tan-1(3/√(16 + x2) ) De snelheid waarmee ∠FCD verandert is gelijk aan de afgeleide daarvan. Voer in je GR in: Y1 = tan-1 (1/√(16 + x2) ) + tan-1(3/√(16 + x2) ) en Y2 = nDerive(Y1, X, X) calc - maximum van Y2 geeft dan (denk erom bij het instellen van WINDOW dat de hoek afneemt dus de afgeleide is negatief): x = 3,15 |
||||
| 4. |
|
||||
| a. | Verplaats
bijvoorbeeld BQ naar HM (M midden van BF) (AH naar BG zou
ook een optie zijn) AM2 = 42 + 22 = 20 dus AM = √20 AH2 = 42 + 42 = 32 dus AH = √32 HM2 = HF2 + FM2 = 32 + 4 = 36 dus HM = 6 cosinusregel in driehoek HMA: 20 = 32 + 36 - 2 • √32 • 6 • cosAHM Dat geeft cos(AHM) = 0,7071 en ∠AHM = 45º |
||||
| b. | Verplaats
bijvoorbeeld BD naar PM (M midden van FG) PM2 = 22 + 22 = 8 dus PM = √8 AP2 = AH2 + HP2 = 32 + 4 = 36 dus AP = 6 AM is gelijk aan AP dus ook 6; driehoek APM is gelijkbenig met tophoek A Als N het midden van PM is, dan is cos(NPA) = PN/PA = 0,5√8/6 = 0,2357 Dus ∠NPA = 76,4º |
||||
| c. | Verplaats
bijvoorbeeld PF naar BM (M midden van DC) en ook AQ naar BN (N
midden van GC). BM2 = 42 + 22 = 20 dus BM = √20 BN2 = 42 + 22 = 20 dus BN = √20 MN2 = 22 + 22 = 8 dus MN = √8 MNB is een gelijkbenige driehoek met zijden √20 en √20 en √8, en het gaat om hoek B Teken de hoogtelijn van B naar het midden P van MN sin(MBP) = 0,5√8/√20 dus ∠MBP = sin-1(0,5√8/√20) = 18,43º Dan is ∠MBN = 2 • 18,43º = 36,87º |
||||
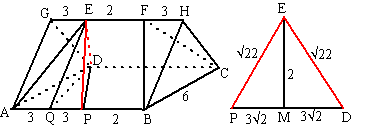
| 5. | a. | Verplaats bijvoorbeeld BF naar EP
(met P op AB zodat PB = 2 en dus AP = 6) Het is handig om het prisma eerst recht te maken: AGD.BHC. AG2 = 32 + 22 = 13 Dus AG = EQ = √13 EP2 = EQ2 + QP2 = 13 + 9 = 22 Dus EP = ED = √22 PD2 = 62 + 62 = 72 dus PD = √72 = 6√2 |
 |
||
| sin(PEM) = 3√2/√22
dus ∠PEM = sin-1(3√2/√22)
= 64,76º Dan is ∠PED = 2 • 64,76º = 129,52º De hoek tussen de rode lijnen is dan 180º - 64,76º = 50,5º |
|||||
| b. |
|
||||
| Verplaats
bijvoorbeeld AC naar BP (zodat CP = 8) BE2 = 52 + 13 = 38 (want EQ = AG = √13) dus BE = √38. BP2 = 82 + 62 = 100 dus BP =10 EP2 = ER2 + RP2 = 13 + 132 = 182 dus EP = √182. cosinusregel in driehoek EBP: 182 = 38 + 100 - 2√38 • 10 • cosEBP Dat geeft cosEBP = -0,3569 en dus ∠EBP = 110,91º Dan is de hoek tussen de rode lijnen gelijk aan 180º - 110,91º = 69,1º |
|||||
| c. | Verplaats bijvoorbeeld BE naar PF
(met PB = 2) PF2 = 52 + QF2 = 25 + 13 = 38 dus PF = √38 DF2 = DG2 + GF2 dus DF is ook √38 PD2 = 102 + 62 = 136 dus PD = √136 Driehoek DFP is gelijkbenig met top F. Teken de hoogtelijn FF' daarin |
|
|||
| sin(F'FP) = F'P/FP
= 0,5√136/√38
= 0,9459 dus ∠F'FP = 71,07º Dan is ∠DFP = 2 • 71,07º = 142,14º De hoek tussen de rode lijnen is 180º - 142,14º = 37,9º |
|||||
| 6. | Als AB = 1 dan
is AH = √2 en HB =
√3 tanAHB = 1/√2 geeft ∠AHB = 35,26º AHC is gelijkzijdig dus ∠AHC = 60º AHF is gelijkzijdig dus ∠AHF = 60º tanBHC = 1/√2, dus ∠BHC = ∠AHB tanBHF = 1/√2 dus ∠BHF = ∠AHB CHF is gelijkzijdig dus ∠CHF = 60º Je vindt dus twee verschillende hoeken. |
||||
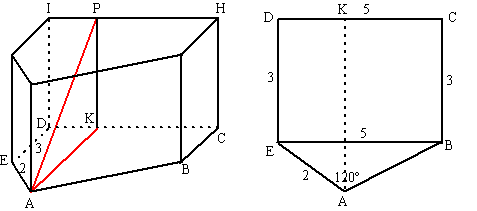
| 7. |
|
||||
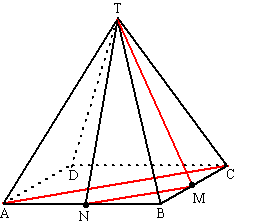
| De hoek zal het
grootst zijn als P het dichtst bij A ligt, en dat is als P recht
tegenover A ligt, dus als de hoek DKA 90º zal zijn. 5/sin120 = 2/sinABE in het bovenaanzicht geeft sinABE = 0,3464 dus ∠ABE = 20,27º Dan is ∠AEB = 180º - 120º - 20,27º = 39,73º sin39,73 = AL/2 geeft AL = 2 • sin39,73 = 1,278 AK = 3 + 1,278 = 4,278 en tanPAK = PK/AK = 3/4,278 = 0,7012 dus ∠PAK = 35,0º is de grootste hoek. De kleinste hoek zul je vinden als P zo ver mogelijk van A af zit, en dat is als P = H cos39,373 = EL/2 geeft EL = 2 • cos39,73 = 1,538 dus KC = 5 - 1,538 = 3,462 AC2 = AK2 + KC2 = 4,2782 + 3,4622 = 30,287 dus AC = 5,503 tanPAK = HC/AC = 3/5,503 = 0,545 dus ∠PAK = 28,6º is de kleinste hoek. |
|||||
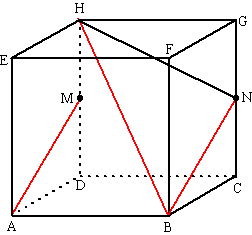
| 8. | a. | Verplaats FK bijvoorbeeld naar BM (M midden
van DC) BM2 = 42 + 22 = 20 dus BM = √20 BE2 = 42 + 42 = 32 dus BE = √32 AM = BM = √20 ME2 = AM2 + EA2 = 20 + 16 = 36 dus ME = 6 cosinusregel in driehoek MBE: 36 = 20 + 32 - 2 • √20 • √32 • cos EBM cosEBM = 0,316 geeft ∠EBM = 71,58º |
|
||
| b. | Verplaats AC bijvoorbeeld naar NM (N midden
van AB) TN2 = TB2 - NB2 = 64 - 16 = 48 dus TN = TM = √48 NM2 = 42 + 42 = 32 dus NM = √32 Driehoek TNM is gelijkbenig met top T. cosTMN = 0,5NM/TM = 0,5√32/√48 = 0,4082 ∠TMN = 65,9º |
|
|||
| c. | Verplaats AM bijvoorbeeld naar BN (N midden
van CG) BN2 = 42 + 22 = 20 dus BN = √20 HN = BN = √20 HB2 = HD2 + DB2 = 16 + 32 = 48 dus HB = √48 driehoek BNH is gelijkbenig met tophoek N. cosHBN = 0,5HB/BN = 0,5√48/√20 = 0,7746 ∠HBN = 39,2º |
|
|||
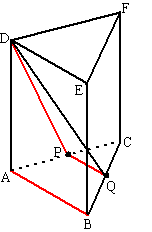
| 9. | Verplaats
bijvoorbeeld AB naar PQ (Q midden van BC) Dan is PQ = 1/2AB = 3 PD2 = 32 + 62 = 45 dus PD = √45 AQ2 = AB2 - BQ2 = 36 - 9 = 27 DQ2 = AD2 + AQ2 = 36 + 27 = 63 dus DQ = √63 cosinusregel in driehoek PQD: 63 = 45 + 9 - 2 • 3 • √45 • cosQPD cosQPD = -0,2236 ∠QPD = 102,92º De hoek tussen DP en PQ is dan 180º - 102,92º = 77,1º |
|
|||
| 10. | Verplaats bijvoorbeeld BG naar MN
(N midden van EH) Neem voor de zijden van de kubus bijvoorbeeld 4. MN2 = 22 + 22 = 8 dus MN = √8 Als N' de projectie van N op AD is, is CN'2 = 42 + 22 = 20 CN2 = CN'2 + NN'2 = 20 + 16 = 36 dus CN = 6 AC2 = 42 + 42 = 32 CM2 = AC2 + AM2 = 32 + 4 = 36 dus CM = 6 |
|
|||
| Driehoek CMN is
gelijkbenig met top C. cosCNM = 0,5NM/CN = 0,5√8/6 = 0,2357 ∠CNM = 76,4º |
|||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||