|
|||||
| 1. |
|
||||
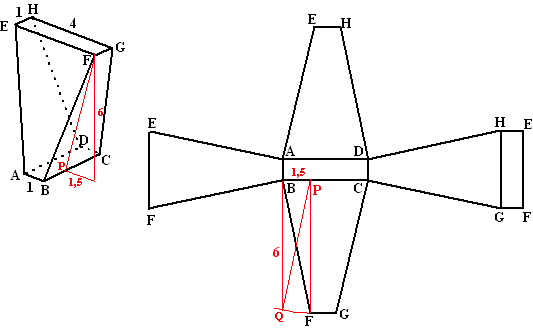
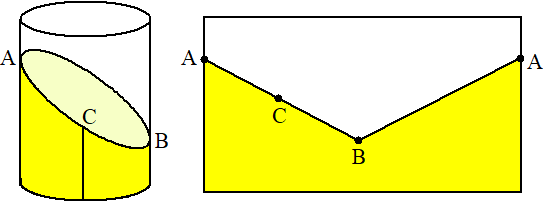
| PF kun je berekenen:
√(1,52 + 62)
≈ 6,18 Je kune het ook construeren: zie de rode hulplijntjes. BP = 1,5. Teken lijn BQ met lengte 6, omcirkel PQ rond P en snij dat met de lijn door P loodrecht op BC. Dat geeft F. |
|||||
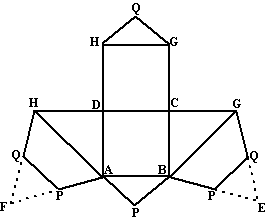
| 2. | Teken vierkanten
ABCD en DCGH DH en CG zijn even lang als de zijde van het vierkant. Driehoek FAH is te maken door cirkels met straal AH en middelpunten H en A met elkaar te snijden. (gelijkzijdige driehoek). Op dezelfde manier BEG. Q en P zijn de middens van FH,FA,BE,GE Tot slot zijn de driehoeken GHQ en ABP te maken door de lengte PQ te omcirkelen vanaf H,G,A en B. |
 |
|||
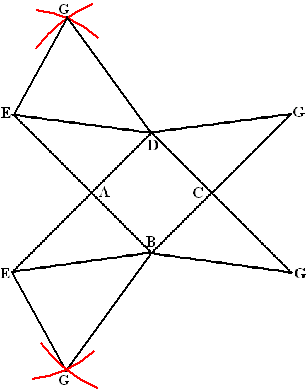
| 3. | Er ontbreken nog
twee vlakken, nl. DEG en BEG. Hoekpunt G kun je vinden door omcirkelen van BG om B en van EG = AC om E. Hoekpunt G kun je ook vinden door omcirkelen van DG om D en van EG =AC om E Dat geeft de volgende tekening: |
||||
|
|
|||||
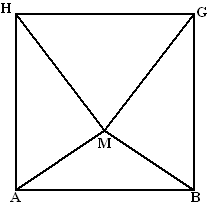
| 4. | a. |
|
|||
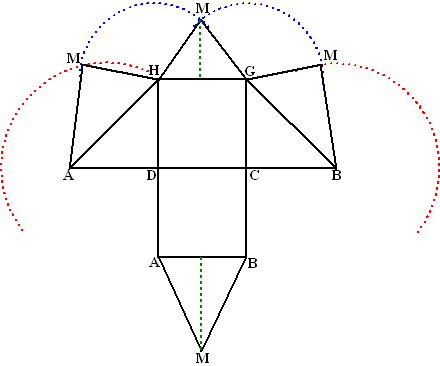
| b. | Zie hieronder. Teken DA = 3 cm en driehoek DAH. Teken CB = 3 cm en driehoek CBG. De groene lijn van M naar het midden van HG heeft lengte 4, dus op schaal is dat 2cm De groene lijn van M naar het midden van AB heeft lengte √(22 + 62) = √40 (dat kun je zien las je in de ruimtelijke figuur van M naar het midden van EF en dan recht omlaag naar het midden van AB een driehoek tekent en Pythagoras gebruikt. Op schaal is dat dan 0,5√40 = 3,2 Teken de rode cirkels met middelpunten B en A en straal BM Teken de blauwe cirkels met middelpunten G en H en straal GM. De snijpunten van de cirkels geven de punten M en dus de vlakken GMB en HMA. |
||||
|
|
|||||
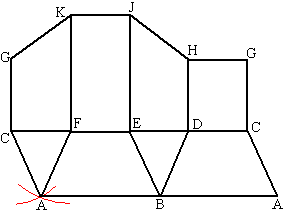
| 5. | zie hiernaast. punt A is gevonden door met middelpunten C en F twee cirkels te tekenen met straal 5. |
 |
|||
| 6. |
|
||||
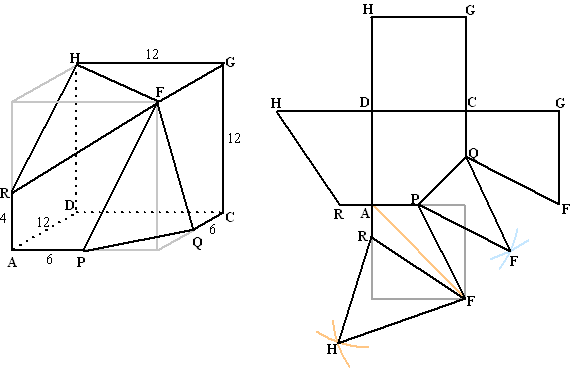
| Teken grondvlak ADCPQ Teken achtervlak DHGC Teken zijvlakken CGFQ en DFRA Teken ARFP (grijze lijnen zijn hulplijnen) tot zover was alles nog uit de oorspronkelijke kubus te herleiden. omcirkel FA om F (FA is even lang als FH) en omcirkel RF om R (RF is even lang als RH) het snijpunt geeft H (oranje lijntjes) en dus vlak RFH omcirkel PF om P en QF om Q het snijpunt (blauwe lijntjes) geeft F en vlak PQF. |
|||||
| 7. | a. | Het is
een halve cilinder plus een prisma. De cilinder heeft straal grondvlak 3 en hoogte ook 3, dus inhoud π • 32 • 3 = 27π. De halve cilinder heeft dus inhoud 13,5π Het prisma heeft als grondvlak een driehoek met oppervlakte 0,5 • 5 • 3 = 7,5 De hoogte is 6, dus de inhoud is 6 • 7,5 = 45 De totale inhoud is dan 45 + 13,5π = 87 cm3 |
|||
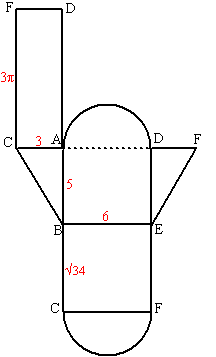
| b. | Zie hiernaast. De
tekening spreekt voor zich, denk ik. BC2 = 52 + 32 dus BC = √34 = 5,83 CF = halve cirkel = 0,5 • (2π•3) = 3π = 9,42 Om BC van vlak BCFE te tekenen kun je de BC van driehoek ABC omcirkelen om B en snijden met het verlengde van AB. |
|
|||
| c. | BPQN
bestaat uit een vierkant MNQP met zijden 3 (straal van de cirkel) en een
driehoek BMN. BM2 = 52 + 32 = 34 dus BM = Ö34. De oppervlakte van de driehoek is dan 0,5 • BM • MN = 0,5 • √34 • 3 De totale oppervlakte is 3 • 3 + 0,5 • √34 • 3 = 18 cm2 |
||||
| 8. |
|
||||
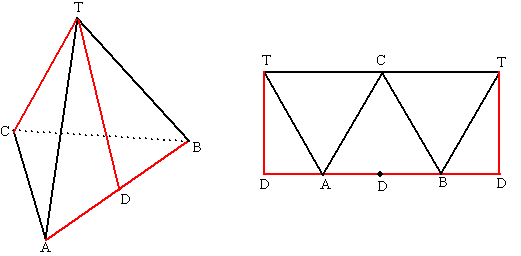
| De opengeknipte
ribben zijn rood gekleurd; daar mag in de uitslag geen ander vlak aan
vastkomen dus. Begin bijv. met een gelijkzijdige driehoek ABC. Aan BC en AC komen twee dezelfde gelijkzijdige driehoeken. Daarna aan AT en BT nog twee halve gelijkzijdige driehoeken. |
|||||
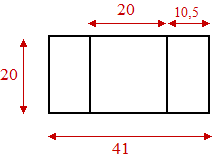
| 9. | a. |
Zie hiernaast met de afmetingen in mm. |
 |
||
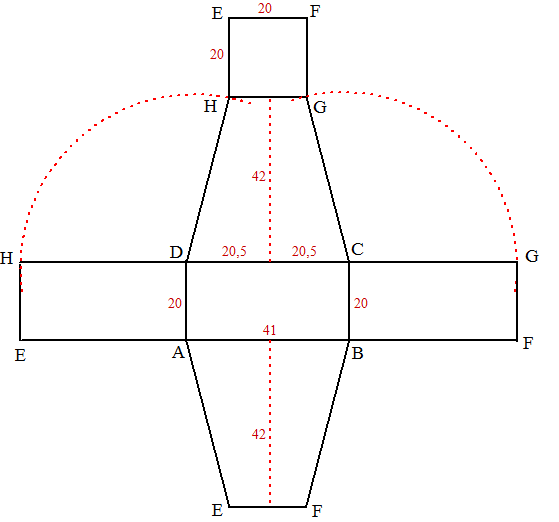
| b. | Zie
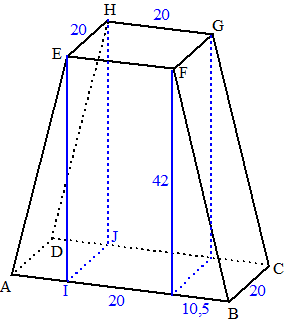
hieronder. De hulplijnen en afmetingen (in mm) staan bij de figuur in het rood. De lengte van CG en DH zijn gevonden door CG en DH om te cirkelen om C en D (zie de cirkelbogen) |
||||
|
|
|||||
| c. | De figuur bestaat
uit een balk met aan beide zijden een prisma. Inhoud balk: 20 • 20 • 42 = 16800 Inhoud prisma: 0,5 • 10,5 • 42 • 20 = 4410 Totale inhoud: 16800 + 2 • 4410 = 25620 mm3 Dat is ongeveer 26 cm3 |
 |
|||
| 10. |
|
||||
| 11. |
 |
||||
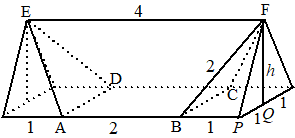
| Zie de figuur. Het
veelvlak is ABCD.EF De diagonaal van een zeshoek is dubbel zo groot als een zijde, dus EF = 4 FP2 = 22 - 12 = 3 dus FP = √3 h2 = FP2 - 12 dus h = √2 Het hele prisma heeft inhoud (0,5 • 2 • √2) • 4 = 4√2 Voor het veelvlak moeten daar twee piramides van af. Een piramide heeft inhoud 1/3 • 2 • 1 • √2 = 2/3√2 Het veelvlak heeft inhoud 4√2 - 4/3√2 = 8/3√2 |
|||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||