|
||||||||
| 1. | a. | De hoogte is 24 en de
straal is 6, dan is de schuine zijde
√(242 + 62) =
√612 De zijde van het karton moet minstens de diameter zijn, en die is 2√612 ≈ 49,5 cm |
||||||
| b. | Er wordt 6/√612
ste deel van de cirkel gebruikt. Dat heeft oppervlakte 6/√612 • π • 612 = 466,31 Het hele karton heeft oppervlakte (2√612)2 = 2448 ze gooit 2448 - 466,31 = 1981,69 weg en dat is 1981,69/2448 • 100% = 81% |
|||||||
| 2. | de omtrek van de
grondcirkel is 70, dus de straal ervan is 70/2π
= 11,14 cm dan is de schuine zijde van de kegel √(11,142 + 182) = 21,17 cm dan is er 11,14/21,17 = 0,526ste deel nodig de oppervlakte is dan 0,526 • π • 21,172 = 740,9 cm2 |
|||||||
| 3. | 0,5 liter is 500 cm3
1/3 • π • r2 • 20 = 500 r2 = 23,87 r = 4,89 cm de schuine kant heeft lengte √(4,892 + 202) = 20,59 cm dan is er 4,89/20,59 = 0,237ste deel nodig de oppervlakte is dan 0,237 • π • 20,592 = 316 cm2 |
|||||||
| 4. | de schuine kant heeft
lengte R = √(r2 +
h2) de hele cirkel van de uitslag heeft omtrek 2πR de grondcirkel heeft omtrek 2πr dus er wordt 2πr/2πR = r/R ste deel gebruikt de oppervlakte is r/R • πR2 = πrR = πr√(r2 + h2) |
|||||||
| 5. | de schuine kant van
de kegel heeft lengte √(82
+ 3,32) = 8,654 m Er is 3,3/8,654 = 0,381ste deel van de uitslagcirkel gebruikt Dat heeft oppervlakte 0,381 • π • 8,6542 = 89,71 m2 Als de dikte overal d is, dan geldt 89,71 • d = 30 d = 0,33 meter, dus dat is 33 cm. |
|||||||
| 6. | hoogte 9,5 en inhoud
515 geeft
πr2 • 9,5 =
515 dan is r2 = 17,25 dus r = 4,15 De manteloppervlakte van het bovenste deel is 2π • 4,15 • 9,5 = 247,95 m2 De bovenkant heeft oppervlakte π • 4,152 = 54,21 De onderkant heeft ook oppervlakte 54,21 maar daar hoeft een deel niet van geverfd te worden De straal van het onderste deel is 0,5 • 4,15 = 2,08 Dus hoeft π • 2,082 = 13,55 m2 niet te worden geverfd, en dus 54,21 - 13,55 = 40,66 m2 wel. De manteloppervlakte van het onderste deel is 2 • π • 2,08 • 41 = 535,06 m2 Dat geeft een totale te verven oppervlakte van 247,95 + 54,21 + 40,66 + 535,06 = 878 m2 |
|||||||
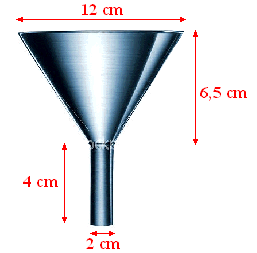
| 7. | de breedte van de afgeknotte kegel loopt van 12 tot 2 over een hoogteverschil van 6,5 cm |
 |
||||||
|
||||||||
| ?? = 7,8 dus de oorspronkelijke kegel was 7,8 cm hoog. | ||||||||
| De straal van het
grondvlak van de kegel is 6 cm. De schuine kant heeft lengte √(62 + 7,82) = √96,84 = 9,84 cm De uitslag van de hele kegel is dan 6/9,84 = 0,6098ste deel van de hele cirkel. De oppervlakte is 0,6098 • π • 9,842 = 185,49 cm2 Het stuk wat er af moet heeft schuine kant √(12 + 1,32) = 1,64 (die 1,3 is natuurlijk 7,8 - 6,5) De oppervlakte is 0,6098 • π • 1,642 = 5,15 Dan blijft over 185,49 - 5,15 = 180,34 |
||||||||
| Het onderste
cilinderdeel moet daar nog bij. Dat heeft oppervlakte 2 • π • 1 • 4 = 25,13 Samen geeft dat oppervlakte 205,5 cm2 |
||||||||
| 8. | De straal van de
grondcirkel is 2 m De schuine kant heeft lengte √(22 + 62) = √40 = 6,32 m De kegeluitslag is dan 2/6,32 = 0,316ste deel van de hele cirkel. De oppervlakte daarvan is 0,316 • π • 6,322 = 39,74 m2 Het topje is een verkleining met factor 1/4 van de hele kegel, dus de oppervlakte ervan is (1/4)2 • 39,74 = 2,48 m2 400 cm2 is 0,04 m2 dus er zijn 2,48/0,04 = 62 donkerblauwe pannen nodig. Het lichtblauwe deel heeft oppervlakte 39,74 - 2,48 = 37,25 m2 dus daar zijn 37,25/0,04 = 931 pannen voor nodig. |
|||||||
| 9. | a. | Als de kleinste
cirkel straal r heeft, dan heeft de grootste cirkel straal r
+ 20 Omdat van beide cirkels hetzelfde deel is getekend (zelfde hoek bij het middelpunt) zijn de verhoudingen tussen de straal en de omtrek gelijk. Dus (r + 20)/125 = r/35 35(r + 20) = 125r 700 = 90r r = 77/9. De hele omtrek van de kleinste cirkel is dan 2π • 77/9 = 48,87 Dus er is 35/48,87 = 0,716 ste deel getekend. De oppervlakte van het grootste cirkeldeel is dan 0,716 • π • (77/9 + 20)2 = 1736,11 De oppervlakte van het kleinste cirkeldeel is dan 0,716 • π • 77/92 = 136,11 De kraag heeft oppervlakte 1736,11 - 136,11 = 1600 cm2 |
||||||
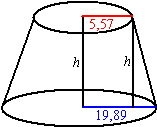
| b. | de schuine kant van de kegel heeft lengte 20 het grondvlak heeft straal 125/(2π) = 19,89 het bovenvlak heeft straal 35/(2π) = 5,57 Dan geldt: h2 + (19,89 - 5,57)2 = 202 h2 = 194,9 h ≈ 14 |
|
||||||
| 10. | De oorspronkelijke
kegel waar de fez van afkomstig is had hoogte 36 (want er moet nog twee
keer 6 van de 12 af om nul te krijgen, dus nog twee keer de hoogte
erbij) De straal van de grondcirkel is 9. Dus is de schuine kant van de kegel √(92 + 362) = √1377 = 37,11 Om de hele kegel te tekenen moet je een cirkel met straal 37,11 tekenen, en daarvan heb je 9/37,11 = 0,2425ste deel nodig. De oppervlakte is dan 0,2425 • π • 37,112 = 1049,20 Om af te knotten moet er nog 0,2425ste deel van een cirkel met straal 2/3 • 37,11 van af (immers het eraf gehaalde deel is 2/3 van de hele kegel). Dat is moppervlakte 0,2425 • π • (2/3 • 37,11)2 = 466,24 Dan blijft voor de fez over 1049,20 - 466,24 = 582,96 cm2 |
|||||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
||||||||