|
|||||
| 1. |
|
||||
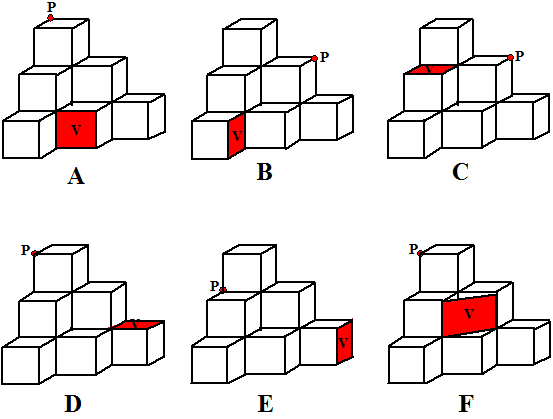
| a. | 8; van P naar V is 2 naar voren | ||||
| b. | 4; van P naar V is 1 naar links | ||||
| c. | '0; P ligt in vlak V | ||||
| d. | 8; van P naar V is 2 omlaag | ||||
| e. | 12; van P naar V is 3 naar rechts | ||||
| f. | 4√2; van P naar V is de diagonaal van een vierkant vlak | ||||
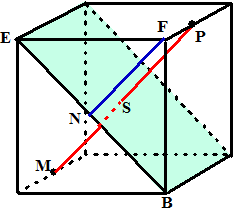
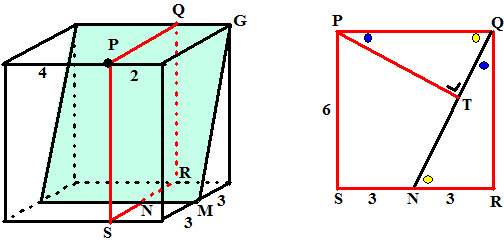
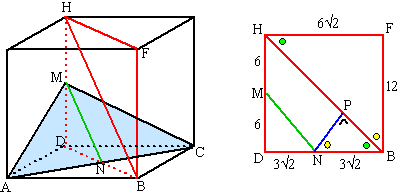
| 2. | a. | PM staat loodrecht op V De afstand van P tot V is PS en is hetzelfde als de lengte van FN (N midden van EB) Die is gelijk aan 1/2EB = 1/2 · 6√2 = 3√2 |
|
||
| b. |
|
||||
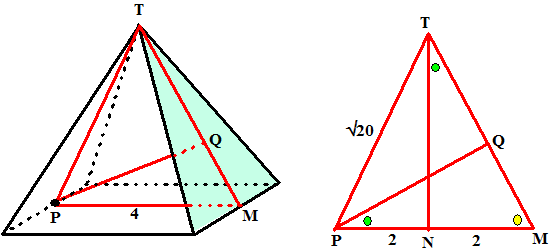
| TP2 = 22
+ 42 = 20 dus TP = √20 De gezochte afstand is PQ (PQ loodrecht op TM) driehoek PQM is gelijkvormig met TNM (rechterfiguur) PQ/PM = TN/TM PQ/4 = 4/√20 PQ = 16/√20 = 3,58 |
|||||
| c. | Teken in lijn in het bovenvlak
van P naar Q (midden van HG), dan staat die loodrecht op het vlak. De gezochte afstand is PS. PS = 1/2PQ en PQ = √(42 + 42) = 4√2 Dus PS = 2√2 |
 |
|||
| d. |
|
||||
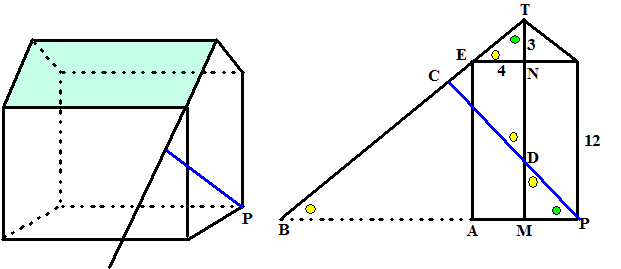
| Verleng de rand van
het dak en trek een lijn PC van P loodrecht naar die rand. De gezochte afstand is PC. Zie de rechterfiguur (zijaanzicht) TEN is gelijkvormig met TBM en met PBC BM/TM = EN/TN dus BM/15 = 4/3 geeft BM = 15 · 4/3 = 20 Dan is BP = 20 + 4 = 24 PC/BP = TN/ET dus PC/24 = 3/4 PC = 24 · 3/4 = 18 |
|||||
| e. |
|
||||
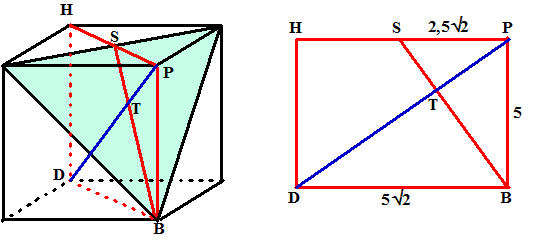
| Het gaat om de
afstand PT in de figuur rechts. NRQ is gelijkvormig met QTP QN2 = 32 + 62 = 45 dus QN = √45 PT/PQ = QR/QN dus PT/6 = 6/√45 en dat geeft PT = 36/√45 = 5,37 |
|||||
| f. |
|
||||
| PD staat loodrecht op
vlak V. Het gaat om de afstand PT. PTS is gelijkvormig met DTB met factor 2. Dus PT = 1/3PD = 1/3 √((5√2)2 + 52) = 1/3 · 5√3 = 5/3√3 = 2,89 |
|||||
| 3. | |||||
|
|
|||||
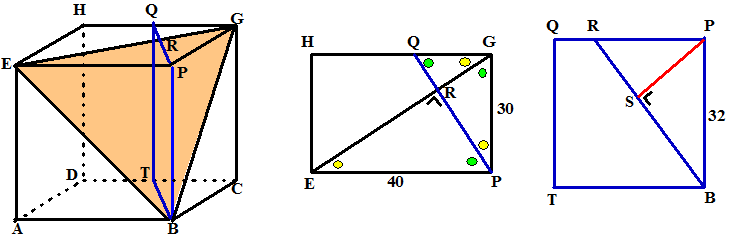
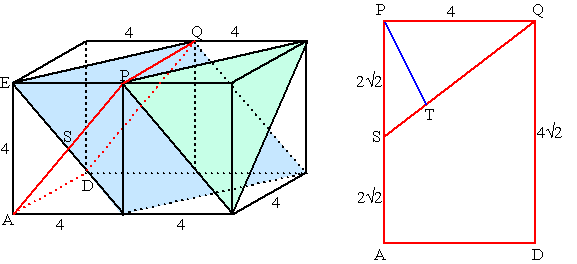
| Teken vlak PQTB zodat
PQ loodrecht op EG staat. QGP is gelijkvormig met GPE QG/GP = GP/PE dus QG/30 = 30/40 en dat geeft QG = 30 · 30/40 = 22,5 QGR is gelijkvormig met GEP dus QR/QG = GP/GE dus QR/22,5 = 30/50 en dat geeft QR = 22,5 · 30/50 = 13,5 PQ2 = QG2 + PG2 dus PQ2 = 22,52 + 302 = 1406,25 dus PQ = √1406,25 = 37,5 Over naar de rechterfiguur: De gezochte afstand is PS (loodrecht op BR en op EG) PR = 37,5 - 13,5 = 24 BR2 = 242 + 322 = 1600, dus BR = 40 De oppervlakte van driehoek PRB is gelijk aan 1/2 · PR · PB maar ook gelijk aan 1/2 · BR · PS Dus 1/2 · 24 · 32 = 1/2 · 40 · PS Dat geeft PS = 19,2 |
|||||
| 4. |
|
||||
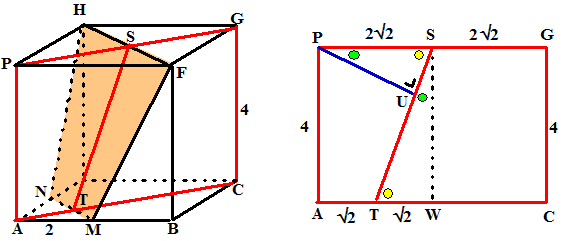
| Teken vlak PGCA
loodrecht op HF. Dan is PS = 1/2PG = 1/2 · 4√2 = 2√2 AT = 1/4AC = 1/4 · 4√2 = √2 Zie de rechterfiguur Teken in vlak PGCA een lijn PU loodrecht op ST De gezocht afstand is PU (loodrecht op ST en op HF) PUS is gelijkvormig met SWT en ST = √(42 + √22) = √18 PU/PS = SW/ST dus PU/2√2 = 4/√18 en dat geeft PU = 2√2 · 4/√18 = 22/3. |
|||||
| 5. |
|
||||
| Teken hulpvlak HFBD De snijlijn van de vlakken is MN (M en N middens van de ribben) HB is evenwijdig aan MN (zie de rechterfiguur: MN is "middenparallel van driehoek HDB) De gezocht afstand is NP Driehoek NPB is gelijkvormig met BFH BH = √((6√2)2 + 122) = √216 NP/NB = BF/BH dus NP/3√2 = 12/√216 NP = 3√2 • 12/√216 = 3,46 |
|||||
| 6. |
|
||||
| Neem bijvoorbeeld
punt P van het groene vlak, en ga de afstand van P tot het blauwe vlak
bepalen. teken Hulpvlak PQDA loodrecht op AP Teken lijnstuk PT loodrecht op SQ (zie rechterfiguur) PT staat loodrecht op het blauwe vlak (want loodrecht op ES en op SQ) dus PT is de gevraagde afstand. De oppervlakte van driehoek PQS is 1/2 • PQ • PS en ook gelijk aan 1/2 • SQ • PT SQ = √(42 + (2√2)2) = √24 1/2 • 4 • 2√2 = 1/2 • √24 • PT PT = 2,31 |
|||||
| 7. |
|
||||
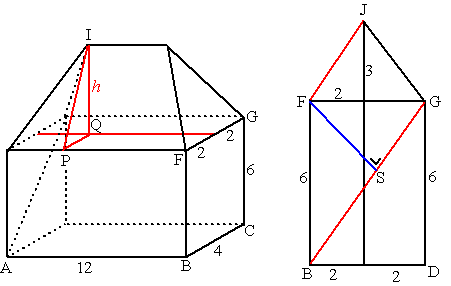
| a. | De vlakken zijn
evenwijdig als IP evenwijdig is aan BG Dan is IQ/QP = BF/BC dus h/2 = 6/4 en dat geeft h = 3 |
||||
| b. | Zie het zijaanzicht
rechts. De rode lijnen zijn evenwijdig. Het gaat om de blauwe afstand FS. De oppervlakte van driehoek FGB is gelijk aan 1/2 • FG • FB maar ook gelijk aan 1/2 • BG • FS BG = √(42 + 62) = √52 1/2 • 4 • 6 = 1/2 • √52 • FS geeft dan FS = 24/√52 = 3,33 |
||||
| 8. |
|
||||
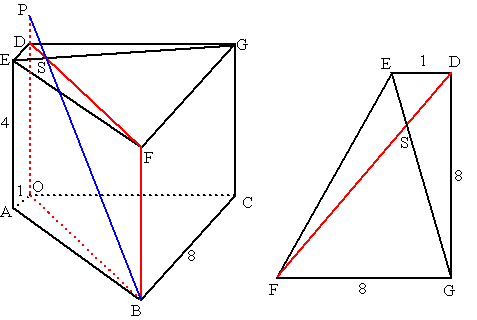
| a. | Teken hulpvlak BODF.
S is het snijpunt van DF en EG. Lijn BS snijdt dan zowel EG (in S) als OD (want ligt in BODF) dus is de gezochte lijn l. Zie het bovenvlak rechts. FD = √(82 + 82) = 8√2 ESD is gelijkvormig met GSF met factor 8. Dus DS = 1/9FD = 8/9√2 In vlak BODF is dan PDS gelijkvormig met POB DS = 8/9√2 en OB = DF = 8√2 Dus DS = 1/9OB Dan is PD = 1/9PO DO = PO - PD = 8/9PO = 4 dus is PO = 41/2 |
||||
| b. |
|
||||
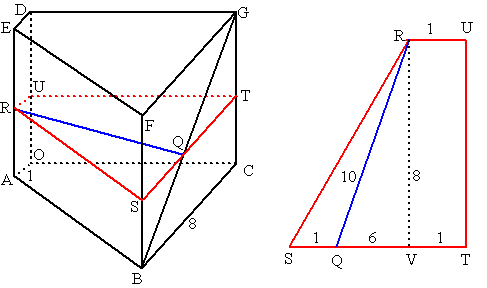
| Teken een horizontaal
vlak TSRU door Q en R Zie de rechterfiguur. QV2 = 102 - 82 = 36 dus QV = 6 en QS = 1 (omdat QV > 1 weten we meteen dat Q inderdaad links van V ligt) In het rechterzijvlak van het prisma is QSB gelijkvormig met QTG QS = 1 en QT = 7 dus de factor is 7 Dan is GT = 7BS, dus BS = 1/8GC = 1/8 • 4 = 1/2 De afstand van QR en ABC is dus 1/2. |
|||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||