|
|||||
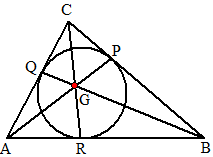
| 1. | a. | AG = AG GR = GQ (straal cirkel) ∠AQG = ∠ARG (rechte hoek cirkel-raaklijn) Dus de driehoeken AQG en ARG zijn congruent (ZZR) Dus is AQ = AR Op precies dezelfde manier zijn de driehoeken BRG en BPG congruent Op precies dezelfde manier zijn de driehoeken CQG en CPG congruent. |
|
||
| b. | AR/RB
BP/PC CQ/QA = AQ/RB RB/PC PC/QA (gebruik het resultaat van vraag a)) = (AQ RB PC)/(RB PC AQ) = 1 Dus gaan de drie lijnen door één punt. |
||||
| 2. | a. | O = 0,5 BC hA
sinC = hA/AC dus hA = AC sinC Dus O = 0,5 BC AC sinC |
|
||
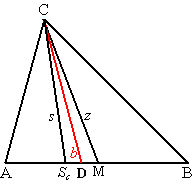
| b. | ∠ACD = ∠BCM (b is bissectrice) ∠ScCD = ∠MCD(s is gespiegelde van z) ∠ACD - ∠ScCD = ∠BCM - ∠MCD ∠ACSc = ∠BCM |
||||
| c. | Oppervlakte ACS is
0,5 AS hC Oppervlakte BMC is 0,5 BM hC De verhouding is dan AS/BM Oppervlakte ACSc is 0,5 AC hS = 0,5 AC CSc sin∠ACSc Oppervlakte BMC is 0,5 BC hM = 0,5 BC CM sin∠BCM Maar omdat die hoeken gelijk zijn, zijn de sinussen ook gelijk Dus de verhouding is (AC CSc)/(BC CM) Die verhoudingen zijn gelijk, dus ASc/BM = (AC CSc)/(BC CM) |
||||
| d. | Oppervlakte ACM is
0,5 AM hC Oppervlakte BCS is 0,5 BSc hC De verhouding is dan AM/BSc Oppervlakte ACM is 0,5 AC hM = 0,5 AC CM sin∠MCA Oppervlakte BCSc is 0,5 BC hM = 0,5 BC CSc sin∠ScCB Maar omdat die hoeken gelijk zijn, zijn de sinussen ook gelijk Dus de verhouding is (AC CM)/(BC CSc) Die verhoudingen zijn gelijk, dus AM/BS = (AC CM)/(BC CSc) |
||||
| e. | De resultaten van
c en d: AS/BM = (AC CSc)/(BC CM) ...(1) AM/BS = (AC CM)/(BC CSc) ...(2) uit (1) volgt: CM/CSc = (AM BC)/(BSc AC) uit (2) volgt: CM/CSc = (BM AC)/(BC ASc) Die moeten dus gelijk aan elkaar zijn; (AM BC)/(BSc AC) = (BM AC)/(BC ASc) Herrangschikken: (AM ASc)/(BSc BM) = AC²/BC² Maar AM = BM want M was het zwaartepunt; dus ASc/BSc = AC²/BC² |
||||
| f. | Op precies dezelfde
manier geldt met de andere zwaartelijnen: vanuit A: CSa/BSa = CA²/BA² vanuit B: ASb/CSb = AB²/CB² Dan geldt: ASc/BSc BSa/CSa CSb/ASb = AC²/BC² BA²/CA² CB²/AB² = 1 De drie lijnen zijn dus Cevianen, dus gaan ze door één punt. |
||||
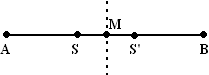
| 3. | Spiegel punt S in M;
dat geeft S' Uit de symmetrie volgt AS = S'B en BS = AS' Dus AS'/S'B = BS/AS = (AS/BS)-1 Alle drie de verhoudingen (in de stelling van Ceva) worden het omgekeerde, dus met elkaar vermenigvuldigd ook, maar dan blijft er 1 uitkomen. Dus zijn de nieuwe lijnen weer Cevianen. |
|
|||
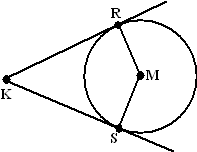
| 4. | a. | KM = KM MR = MS (straal cirkel) ∠MRK = ∠MSK = 90º Dus de driehoeken MRK en MSK zijn congruent Dus is KR = KS |
|
||
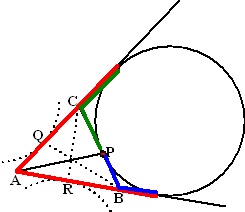
| b. | De regel uit de vorige vraag
betekent dat de rode lijnstukken hiernaast gelijk zijn, en ook de blauwe
en ook de groene. Rood = AB + blauw = AB + BP aan de onderkant Rood = AC + groen = AC + CP aan de bovenkant Dus AB + BP = AC + CP dus P ligt vanaf A halverwege de omtrek van de driehoek ABC. |
 |
|||
| c. | AB + BP = 0,5O dus
BP = 0,5O - AB AC + CP = 0,5O dus CP = 0,5O - AC Dan is BP/CP = (0,5O - AB)/(0,5O - AC) |
||||
| d. | AQ/CQ
= (0,5O - AB)/(0,5O - BC) AR/BR = (0,5O - AC)/(0,5O - BC) AR/RB BP/PC CQ/QA = (0,5O - AC)/(0,5O - BC) (0,5O - AB)/(0,5O - AC) (0,5O - BC)/(0,5O - AB) = 1 Kortom: het zijn Cevianen; dus gaan ze door één punt. |
||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||