|
|||||
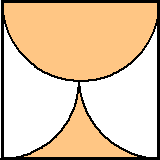
| 1. | Als de
verhouding 23 : 9 is, dan is het eigeel 9/32
deel van het totaal (en het eiwit 23/32 deel) De totale oppervlakte is πr2 = π 22 = 12,57 Het eigeel heeft dus oppervlakte 9/32 12,57 = 3,53 Als de straal van het eigeel r is, dan geldt er dus πr2 = 3,53 r2 = 3,53/π = 1,125 ⇒ r = √1,125 = 1,06 De diameter is dan 2 1,06 = 2,1 cm |
||||
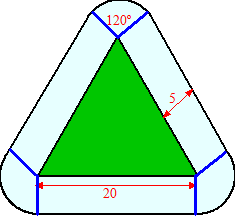
| 2. | Drie rechthoeken van
5 bij 20 geeft 300 km2 Drie cirkeldelen van elk 120š is precies een hele cirkel met straal 5 km. Dat is π 52 = 78,5 km2 Samen geeft dat 378,5 km2 |
 |
|||
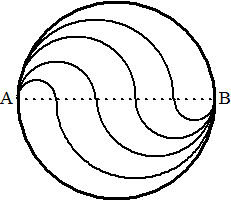
| 3. | Noem de middellijn M,
en verdeel die in n gelijke stukken. Noem die punten P1 tot en met Pn (vanaf A naar B) Het deel boven AB: De halve cirkel van Pi naar A heeft middellijn i M/n en dus straal 0,5i M/n De oppervlakte daarvan is 0,5 π (0,5i M/n)2 = 1/8 π i2 Mē/nē De halve cirkel van Pi - 1 naar A moet daar nog vanaf. Dat is 0,5 π (0,5(i - 1) M/n)2 = 1/8 π Mē/nē (i2 - 2i + 1) Samen geeft dat 1/8 π Mē/nē (2i - 1) Het deel onder AB De halve cirkel van Pi naar B heeft middellijn (n - i) M/n en dus straal 0,5 (n - i) M/n. De oppervlakte daarvan is 0,5 π (0,5 (n - i) M/n)2 = 1/8 π Mē/nē (n - i)2 De halve cirkel van Pi + 1 naar B moet daar nog vanaf Dat is 0,5 π (0,5 (n - i + 1) M/n)2 = 1/8 π Mē/nē ((n - i)2 - 2(n - i) + 1) Samen geeft dat 1/8 π Mē/nē ( 2(n - i) + 1) Beide delen samen. 1/8 π Mē/nē (2i - 1) + 1/8 π Mē/nē ( 2(n -i) + 1) = 1/8 π Mē/nē (2i - 1 + 2n - 2i + 1) = 1/8 π Mē/nē 2n = 1/4 π Mē/n = 1/n (1/4πM2) en dat is inderdaad 1/n ste deel van de hele cirkel. |
 |
|||
| 4. | Het gele deel is wat je krijgt
als twee kwartcirkels elkaar overlappen in een vierkant (zijde 1). Het
gele deel is hoeveel die beide kwartcirkels samen meer zijn dan het
vierkant. De cirkels hebben oppervlakte 0,5πr2 = 0,5π Het vierkant heeft oppervlakte 1 Het gele deel heeft dus oppervlakte 0,5π - 1 De totale gele oppervlakte is dan vierkant - 8 halve cirkels + 8 gele citroenen (want die zijn er elk tweemaal afgehaald) = 16 - 8 0,5π 12 + 8(0,5π - 1) = 16 - 4π + 4π - 8 = 8 |
|
|||
| 5. | Neem als zijde van het vierkant
1. Het bovenste deel is een halve cirkel met straal 0,5 dus oppervlakte 0,5 π 0,52 = 1/8π
Het onderste deel is de helft van wat je overhoudt als je twee halve
cirkels van het vierkant afhaalt. |
|
|||
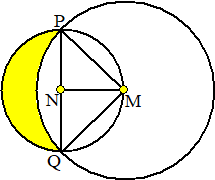
| 6. | Noem de middelpunten
van de cirkels M en N. Omdat PQ een middellijn is, is hoek PMQ 90š. De oppervlakte van het cirkelsegment MPQ van de grote cirkel is 1/4πr2 MN = NP = 1/2r√2 (45-45-90 driehoeken) De oppervlakte van driehoek MPQ is 1/2 r√2 1/2r√2 = 1/2r2 Het cirkelsegment min de driehoek heeft dan oppervlakte 1/4πr2 - 1/2r2 Het maantje heeft oppervlakte de helft van de kleine cirkel min dit laatste deel. 1/2 π (1/2r√2)2 -- 1/4πr2 + 1/2r2 = 1/2r2 |
|
|||
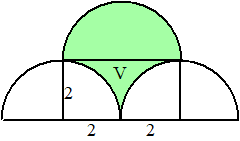
| 7. | Gebied V hiernaast is
een rechthoek min twee kwartcirkels. De opp. van V is 8 - 1/2 π 22 = 8 - 2π Het groene deel is V plus een halve cirkel De opp. is 1/2 π 22 + 8 - 2π = 8 |
|
|||
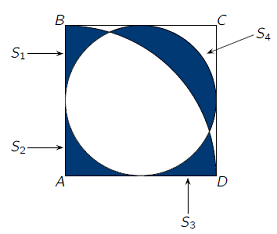
| 8. | de kwartcirkel heeft
straal oppervlakte 0,25π de ingeschreven cirkel heeft straal 0,5 en oppervlakte 0,25π kwartcirkel - S1 - S2 - S3 = ingeschreven cirkel - S4 S1 + S2 + S3 - S4 = kwartcirkel - ingeschreven cirkel S1 + S2 + S3 - S4 = 0,25π - 0,25π = 0 |
 |
|||
|
Đ h.hofstede (h.hofstede@hogeland.nl) |
|||||