|
|||||
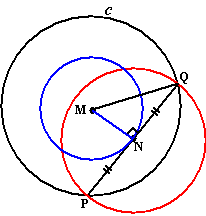
| 1. | De straal van de rode
cirkel is NP De straal van de blauwe cirkel is MN De straal van cirkel c is MQ Pythagoras in driehoek MNQ: MN2 + NQ2 = MQ2 Vermenigvuldig alles met π: πMN2 + πNQ2 = πMQ2 Daar staat: oppervlakte blauw + oppervlakte rood = oppervlakte c |
|
|||
| 2a. | M1M2Q
is een gelijkzijdige driehoek met zijden 3. Voor de hoogte h daarvan geldt h2 = 32 - 1,52 = 63/4 h = √(63/4) = √(27/4) = 1/2√27 = 3/2√3 oppervlakte is 1/2 • 3 • 3/2√3 = 21/4√3 de oppervlakte van het parallellogram is dan 2 • 21/4√3 = 41/2√3 |
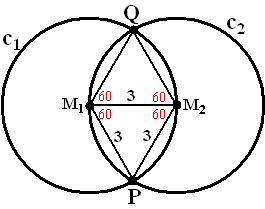 |
|||
| 2b. | Een cirkelsector M1QP
heeft hoek 120º De oppervlakte daarvan is dan 1/3 • π • 32 = 3π De beide cirkelsectoren hebben samen oppervlakte 6π Daar moet het parallellogram vanaf, want dat is dubbel geteld. Dan blijft over 6π - 41/2√3 |
||||
| 3. | De kleine cirkel kan
overal in het gebied komen dat door de middelste cirkel wordt doorlopen. Dat is het gebied tussen de buitenste cirkel met straal R en de zwarte binnenste cirkel met straal R/3 Die oppervlakte is πR2 - π(R/3)2 = πR2 - 1/9πR2 = 8/9πR2 |
|
|||
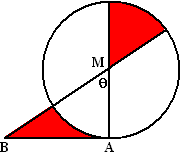
| 4. | De bovenste rode
oppervlakte is θ/360
•
πR2 AB = Rcosθ, dus de driehoek ABM heeft oppervlakte 1/2 • Rtanθ • R Als de rode oppervlaktes gelijk zijn, dan is de oppervlakte van ABM het dubbele van die rode oppervlakte. Dus 1/2 • Rtanθ • R = 2• θ/360 • πR2 1/2 • tanθ = 2 • θ/360 • π Invoeren in de GR en dan intersect levert θ ≈ 67º |
|
|||
| 5. | De rode cirkelsector
hiernaast heeft middelpuntshoek 60º De oppervlakte daarvan is dan 1/6 • π • 1802 = 5400π De drie sectoren hebben samen dan oppervlakte 3 • 5400π = 16200π Maar dan is die gelijkzijdige driehoek in het midden drie keer meegeteld. Die driehoek heeft zijden 180 Voor de hoogtelijn h geldt dan h2 = 1802 - 902 = 24300 h = √(24300) = 90√3 De oppervlakte is 1/2 • 90√3 • 180 = 8100√3 |
|
|||
| De roestvrijstalen
oppervlakte in het ondervlak is dan 16200π
- 2 • 8100√3 =
22834, 5779 De roestvrijstalen oppervlakte in het bovenvlak is dan 22834,5779 - π • 552 = 13331,2601 |
|||||
| De omtrek van het
bovenoppervlak bestaat uit 3 delen die elk 1/6
cirkel zijn. Samen is dat een halve cirkel: omtrek π • 180 De oppervlakte van de gebogen zijkant van de urn is dan π • 180 • 400 = 226194,6711 Samen geeft dat roestvrijstalen oppervlakte 22834,5779 + 13331,2601 + 226194,6711 = 262360,5 mm2 Dat is ongeveer 2624 cm2 |
|||||
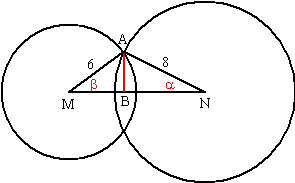
| 6. | Zie de figuur
hiernaast. cosinusregel: 62 = 82 + 122 - 2 • 8 • 12 • cosα cosα = 0,8958 α = 26,38º De oppervlakte van cirkelsector vanuit N is dan 26,38/360 • π • 82 = 14,7358 82 = 62 + 122 - 2 • 6 • 12 • cosβ cosβ = 0,8056 β = 36,34º De oppervlakte van cirkelsector vanuit M is dan 36,34/360 • π • 62 = 11,4153 |
 |
|||
| AB = 6sinb
= 3,55 Oppervlakte driehoek MNA is 1/2 • 12 • 3,55 = 21,3307 Het gedeelte binnen beide cirkels is 14,7358 + 11,4153 - 21,3307 = 4,8204 Het gehele overlappende cirkeldeel is dan 2 • 4,8204 ≈ 9,64 |
|||||
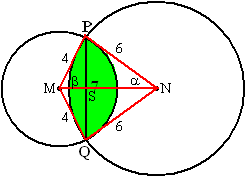
| 7. | Zie de tekening
hiernaast. BS = SQ = 3,5 sinα = 3,5/6 ⇒ α = 35,69º sinβ = 3,5/4 ⇒ β = 61,04º SN = 6cosα = 4,87 SM = 4cosβ = 1,94 MN = 4,87 +1,94 = 6,81 De oppervlakte van driehoek MNP is 1/2 • 6,81 • 3,5 = 11,92 De cirkelsector vanaf N met hoek α heeft oppervlakte 35,69/360• π • 62 = 11,21 De cirkelsector vanaf M met hoek β heeft oppervlakte 61,04/360 • π • 42 = 8,52 |
|
|||
| Tel beide
cirkelsectoren op en trek driehoek MNP er weer af. Dat geeft oppervlakte
7,82 De oppervlakte van het deel binnen beide cirkels is dan 2 • 7,81 = 15,63 |
|||||
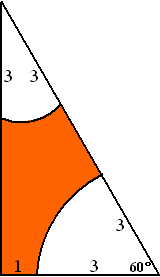
| 8. | De driehoek heeft
hoeken van 30º en 60º en 90º Het bovenste cirkeldeel heeft oppervlakte 30/360 • π • 32 = 3/4π Het onderste cirkeldeel heeft oppervlakte 60/360 • π • 32 = 11/2π Als de rechtopstaande zijde lengte x heeft, dan geldt tan60º = x/4 x = 4 • tan60º = 4√3 De oppervlakte van de driehoek is dan 1/2 • 4 • 4√3 = 8√3 Het gekleurde deel heeft oppervlakte 8√3 - 21/4π |
|
|||
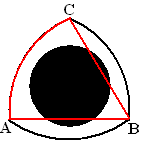
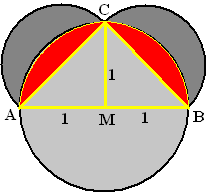
| 9. | Omdat de randen halve
cirkels zijn is AC een middellijn van zo'n kleinere cirkel. AC2 = 12 + 12 ⇒ AC = √2 De straal van een kleinere cirkel is dus 1/2√2 Twee zulke halve cirkels hebben samen oppervlakte π•(1/2√2)2 = 1/2π Driehoek ABC heeft oppervlakte 1/2 • 2 • 1 = 1 Samen geeft dat oppervlakte 1 + 1/2π Daar moet nog de onderste helft van die grote cirkel bij. 1 + 1/2π + 1/2 • π • 12 = 1 + π is dan de totale oppervlakte |
|
|||
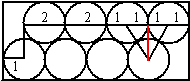
| 10. | a. | eerste methode: de
rechthoek is 8 bij 4 en heeft dus oppervlakte 32 tweede methode: zie de figuur hiernaast. het rode lijnstukje is de hoogtelijn in een gelijkzijdige driehoek met zijden 2. Voor de lengte h geldt dan h2 = 22 - 12 = 3 Dus h = √3 De breedte van de rechthoek is 9, de hoogte is 2 + √3 De oppervlakte is dan 9 • (2 + √3) ≈ 33,6 |
|
||
| b. | Bij 2n cirkels
liggen er n naast elkaar. de eerste methode geeft een rechthoek van 2n bij 4 dus oppervlakte 8n de tweede methode geeft een rechthoek van 2n + 1 bij 2 + √3 dus oppervlakte (2n + 1)(2 + √3) |
||||
| c. | 8n = (2n
+ 1)(2 + √3) 8n = 4n + 2n√3 + 2 + √3 n(4 - 2√3) = 2 + √3 n = (2 + √3)/(4 - 2√3) = 6,96 vanaf 14 cirkels (n = 7) is methode 2 goedkoper. |
||||
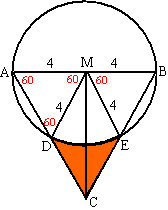
| 11. | MC2 = 82
- 42 = 48 dus MC = 4√3
omdat ∠MAD = 60º en MA = MD zijn de driehoeken MAD en MEB ook gelijkzijdig. Oppervlakte MDCE is 1/2 • DE • 1/2MC • 2 = 4 • 2√3 = 8√3 Oppervlakte cirkeldeel MDE is 60/360 • π • 42 = 22/3π Het gekleurde deel heeft dan oppervlakte 8√3 - 22/3π |
|
|||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||