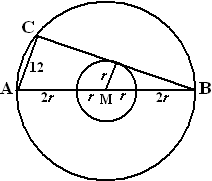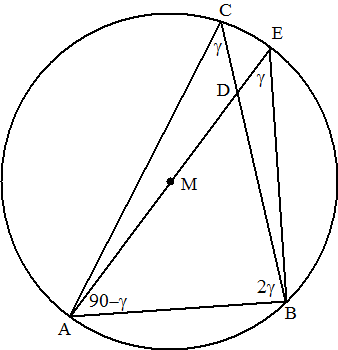|
|||||
| 1. | Gelijkvormigheid
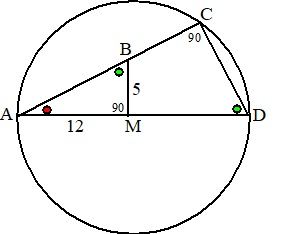
levert r/2r = 12/6r Daaruit volgt r = 6 Omdat AB een middellijn is, is hoek ACB 90º. Pythagoras: 122 + BC2 = 362 Daaruit volgt BC = √1152 = 24√2 |
|
|||
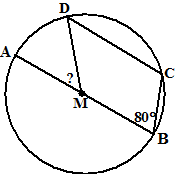
| 2 | Teken lijnstuk AC. ∠ACB = 90º want AB is een middellijn. Dan is ∠MAC = 10º (hoekensom driehoek ACB) Dan is ∠DCA = 10º (Z-hoeken want DC//AB) Dan is ∠DMA = 20º want het is de middelpuntshoek van koorde AD, en de omtrekshoek daarvan is ∠DCA = 10º |
|
|||
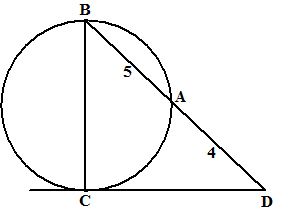
| 3. | Teken lijnstuk AC. Dan is ∠CAB = 90º (BC is een middellijn) ÐBCD is ook 90º (raaklijn aan een cirkel) Dan zijn de driehoeken BAC en BCD gelijkvormig (beiden ∠B en een rechte hoek) BA/BC = BC/BD 5/BC = BC/9 BC2 = 45 ⇒ BC = √45 CD = √(92 - 45) = √36 = 6 |
|
|||
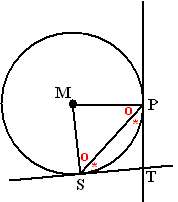
| 4. | a. | Omdat P en S op een
cirkel liggen is MP = MS Dus driehoek MPS is gelijkbenig. Dan is ∠MSP gelijk aan ∠MPS. Omdat T op de raaklijn ligt is ∠MPT = 90º en ook ∠MST = 90º. Dus zijn de hoeken TPS en TSP óók gelijk Dus is driehoek TSP óók gelijkbenig, Dus is TP = TS In de andere cirkel geldt op precies dezelfde manier dat TS = TQ. Conclusie: TS = TP = TQ dus de punten P, Q en S liggen even ver van T, dus op een cirkel met T als middelpunt. |
|
||
| b. | ∠RSQ
is 90º (Thales) P,Q en S liggen op cirkel met middelpunt T (vraag a), dus ook ∠QSP is 90º (Thales) Dus ∠RSP = 90º + 90º = 180º dus R,S en P liggen op één lijn. |
||||
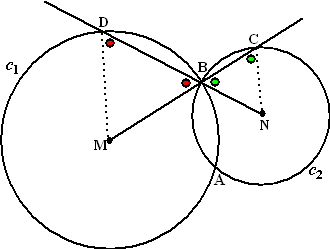
| 5. | Zie de figuur
hiernaast. De rode hoeken zijn gelijk (MB = MD = straal cirkel, dus MDB is gelijkbenig) De groene hoeken zijn gelijk (hetzelfde in de andere cirkel) Maar een rode hoek is gelijk aan een groene hoek (overstaande hoeken bij B) Dus is de groene hoek bij C gelijk aan de rode bij D. Dus liggen D en C op een cirkel met middellijn MN (Thales) Dus liggen D, C, M en N allemaal op die cirkel. |
|
|||
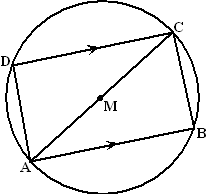
| 6. | a. | Omdat
AC een middellijn van een cirkel is, geldt (stelling van Tales) dat
∠ADC = 90º ∠BAC = ∠ACD (Z-hoeken) Dus zijn de driehoeken ADC en CBA congruent (HHZ). ∠DAC + ∠ACD = 90º (hoekensom driehoek ADC) ∠ACD = ∠BAC, dus ook ∠DAC + ∠BAC = 90º Dus is ∠DAB = 90º, En dus is de vierde hoek (∠DCB) ook 90º. |
|
||
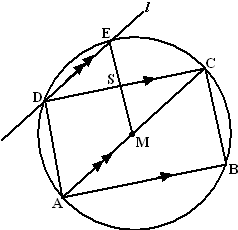
| b. |
∠CSE is de buitenhoek van driehoek DSE, dus ∠CSE = ∠CDE + ∠DEM ......(1) ∠DEM = ∠CME (Z-hoeken) ......(2) ∠CME is de middelpuntshoek van koorde CE, dus is gelijk aan het dubbele van de omtrekshoek, en dat is ∠CDE, dus ∠CME = 2 • ∠CDE ......(3) eerst (2) en dan (3) invullen in (1) geeft ∠CSE = ∠CDE + ∠CME = ∠CDE + 2 • ∠CDE = 3 • ∠CDE |
|
|||
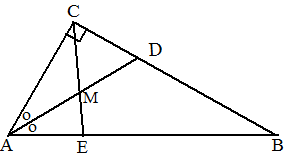
| 7. | M is middelpunt van AD en
∠ACD = 90º dus is M middelpunt van een
cirkel door A, C en D (Thales) Dus is MA = MC (straal cirkel) Dus driehoek MAC is gelijkbenig en ÐMCA = ∠MAC = o Dan is ∠BEC = ooo (buitenhoek van driehoek AEC. |
|
|||
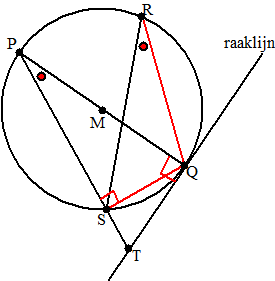
| 8. | ∠QRS = ∠QPS (omtrekshoek van koorde QS) ∠PSQ = 90º (Thales) ∠SQR = 90º (raaklijn. Dus de driehoeken SQR en QTP zijn gelijkvormig (hh) Dan is PQ/ PT = PS/PQ Daaruit volgt PQ • PQ = PS • PT PQ = d dus d2 = PS • PT |
|
|||
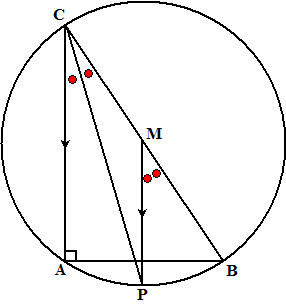
| 9. | Vanwege de rechthoekige driehoek
is er een cirkel met middelpunt M en middellijn BC die door A gaat (Thales) Stel dat de bissectrice deze cirkel in P snijdt. Dan is de middelpuntshoek van koorde PB gelijk aan hoek C van de driehoek. Maar dan zijn MP en CA evenwijdig (F-hoeken) Dus ligt P ook op de lijn door M evenwijdig aan AC. |
|
|||
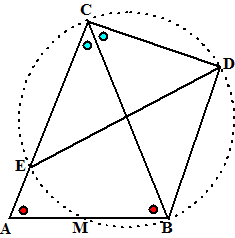
| 10. | a. | ∠CDB is 90º dus BC is een middellijn van cirkel c (Thales) Maar ∠BMC is ook 90º (gelijkbenige driehoek ABC) dus die cirkel met middellijn BC gaat ook door M |
|
||
| b | De omtrekshoeken van koorden BD
en EB zijn gelijk (bissectrices bij C) Dus de middelpuntshoeken ook. Noem het snijpunt van ED en BC punt S. Dus ∠ESB = ∠DSB Maar samen zijn ze 180º dus is elk 90º |
||||
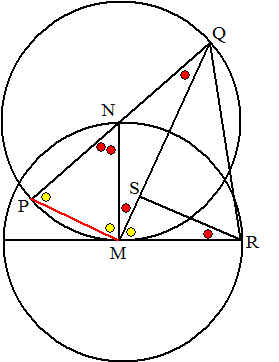
| 11. | ∠MNP = 2 • ∠MQN (omtrekshoek en middelpuntshoek
PM) Driehoek MPM is gelijkbenig dus de gele basishoeken zijn gelijk Dan geeft de hoekensom van die driehoek dat geel + rood = 90º ∠QMN = ∠NQM (gelijkbenige driehoek) ∠PMQ = 90º (Thales) Daaruit volgt dat ∠RMS = ∠NPM De driehoeken PMQ en MSR zijn gelijkvormig. Omdat PQ = 2 • MR is dus ook MQ = 2 • RS qed. |
|
|||
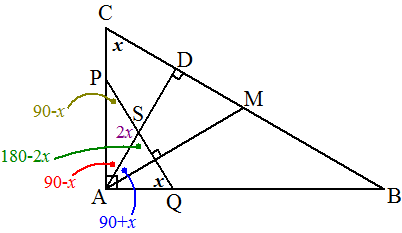
| 12. | Stel hoek C is x,
dan kun je het volgende rijtje hoeken in x uitdrukken: ∠CAM = x (Thales; AC = AM) ∠CAD = 90 - x (hoekensom CAD) ∠DAM = 90 + x (∠CAM - ∠CAD) ∠ASQ = 180 - 2x (hoekensom driehoek) ∠ASP = 2x (gestrekte hoek) ∠APS = 90 - x (hoekensom driehoek APS) Dus driehoek ASP is gelijkbenig en SP = SA .....(1) ∠AQP = x (hoekensom APQ) ∠SAQ = x (hoekensom ASQ) Dus driehoek ASQ is gelijkbenig en AS = SQ ...(2) Uit (1) en (2) volgt dat SP = SQ |
 |
|||
| 13. | ∠AEB =
γ
(omtrekshoek AB) ∠ABE = 90º (Thales) ∠BAE = 90 - γ (hoekensom ABE) ∠ADB = 180 - (90 - γ) - 2γ = 90 - γ Dus ∠ADB = ∠BAE Dus driehoek BAD is gelijkbenig (gelijke basishoeken) |
|
|||
| 14. | a. | MP' • MP = 1 = MQ'• MQ Dus MQ'/MP' = MP/MQ De hoeken Q'MP' en QMP zijn gelijk. Dus zijn de driehoeken gelijkvormig (zhz) |
|
||
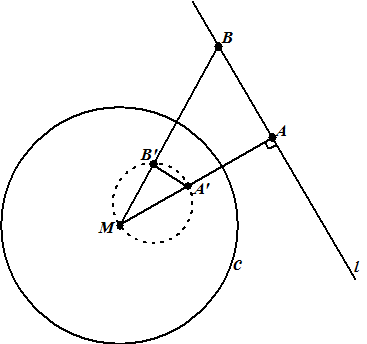
| b. | De
driehoeken MB'Á' en MAB zijn gelijkvormig (zie de vorige vraag) Dus is ∠MB'A'= ∠MAB = 90º Dan is MA' middellijn van een cirkel waar ook B' op ligt (stelling van Thales) |
||||
| 15, | Verleng AM tot AD. Dan is hoek ACD = 90 (Thales) Dus de driehoeken ABM en ADC zijn gelijkvormig AB = 13 (Pythagoras), en AD = 24 13/24 = 12/AC geeft dan AC = 12 • 24/13 = 288/13 |
|
|||
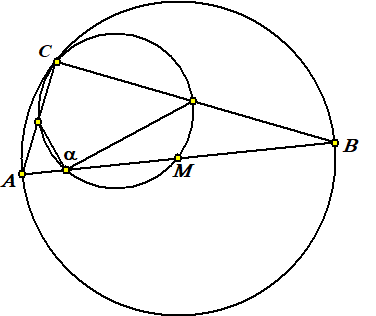
| 16. | AB is een middellijn
dus de hoek bij C is recht Dus is hoek C in de kleine cirkel ook recht Dus staat hoek C op een middellijn van de kleine cirkel. Dat doet hoek a ook, dus hoek a is ook recht. |
 |
|||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||