|
|||||
| 1. | a. | 2x2 + 5y2 =
88 in het punt P(-2, 4) 4x + 10yy' = 0 y ' = -4x/10y in P is de helling dan 8/40 = 0,2 4 = 0,2 -2 + b geeft b = 4,4 De raaklijn is y = 0,2x + 4,4 |
|||
| b. | 6x2 + 3y2 -
81 = 0 in het punt P(-1, -5) 12x + 6yy' = 0 y' = -12x/6y in P is de helling 12/-30 = -0,4 -5 = -0,4 -1 + b geeft b = -5,4 De raaklijn is y = -0,4x - 5,4 |
||||
| c. | y2 + 2x2 + 8y
- 4x + 12 = 0 in het punt P(2, -2) 2yy' + 4x + 8y' - 4 = 0 y'(2y + 8) = 4 - 4x y' = (4 - 4x)/(2y + 8) in P is de helling -4/4 = -1 -2 = -1 2 + b geeft b = 0 De raaklijn is y = -x |
||||
| d. | 2(y + 3)2 + 3(x - 1)2
= 29 in het punt P(4, -2) 4(y + 3)y' + 6(x - 1) = 0 y ' = -6(x - 1)/4(y + 3) in P is de helling -18/4 = -4,5 -2 = -4,5 4 + b geeft b = 16 De raaklijn is y = -4,5x + 16 |
||||
| 2. | a. | x²/15
+ y²/10
= 1 in het punt P(3, -2) 2x2 + 3y2 = 30 4x + 6yy' = 0 y' = -4x/6y in P is de helling -12/-12 = 1 loodrecht daar op staat helling -1 -2 = -1 3 + b geeft b = 1 de normaal is de lijn y = -x + 1 |
|||
| b. | 4(x + 1)2 = 41 - y2 in het punt P(-3, 5) | ||||
| 8(x + 1) = -2yy' y' = 8(x + 1)/-2y in P is de helling -16/-10 = 8/5 loodrecht daar op staat helling -5/8 5 = -5/8 -3 + b geeft b = 25/8 de normaal is de lijn y = -5/8x + 25/8 |
|||||
| 3. | a. | ax2
- 10x + 2y2 = 8. 2ax - 10 + 4yy' = 0 y' = (10 - 2ax)/4y = 2 10 - 2ax = 8y maar omdat y = 2x geldt 10 - 2ax = 16x 2ax = 10 - 16x a = 5/x - 8 |
|||
| b. | a = 5/x - 8
en y = 2x invullen in de ellipsvergelijking: (5/x - 8)x2 - 10x + 2(2x)2 = 8 5x - 8x2 - 10x + 8x2 = 8 -5x = 8 x = -1,6 a = 5/-1,6 - 8 = -111/8 |
||||
| c. | y = 2x invullen in
de ellips: ax2 -10x + 2(2x)2 = 8 (a + 8)x2 - 10x - 8 = 0 Discriminant is nul: 100 + 32(a + 8) = 0 100 + 32a + 256 = 0 32a = -356 a = -11,125 |
||||
| 4. | a. | 2x2
+ y2 = 81 4x + 2yy' = 0 y ' = -4x/2y = 4 8y = -4x x = -2y invullen in de ellipsvergelijking: 2(-2y)2 + y2 = 81 9y2 = 81 y2 = 9 y = ±3 y = 3 geeft x = -6 en dan is 3 = 4 -6 + b dus b = 27 en de raaklijn is y = 4x + 27 y = -3 geeft x = 6 en dan is -3 = 4 6 + b dus b = -27 en de raaklijn is y = 4x - 27 |
|||
| b. | Het gaat bijvoorbeeld om de afstand d van (6, -3) tot de lijn y = 4x + 27 (dat is de lijn -4x + y - 27 = 0) | ||||
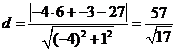 |
|||||
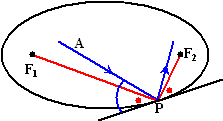
| 5. | Zie hiernaast de
situatie voor een straal tussen de brandpunten door. Stel dat die de
ellips in P raakt. Teken ook F1P en F2P Die maken gelijke hoeken met de raaklijn (de rode hoeken hiernaast) Maar de straal A moet σσk gelijke hoeken met de raaklijn maken. Aan de ene kant is die blauwe hoek groter dan de rode, dus aan de andere kant ook, dus blijft de straal tussen de brandpunten doorgaan. |
|
|||
| Voor straal B geldt het zelfde verhaal, maar moet je groter/kleiner door kleiner/groter vervangen. | |||||
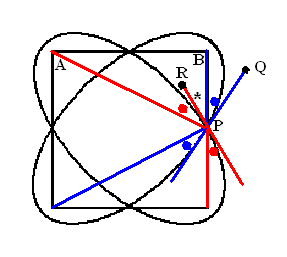
| 6. | Vanwege de
raaklijneigenschappen van een ellips zijn de rode hoeken aan elkaar
gelijk en de blauwe ook. Vanwege de symmetrie van de figuur is een rode hoek gelijk aan een blauwe. Daarom is hoek QPR = hoek BPA (beide een rood/blauwe plus de hoek met het sterretje) tan BPA = 4/2 = 2 ⇒ BPA = 63Ί |
|
|||
| 7. |
|
||||
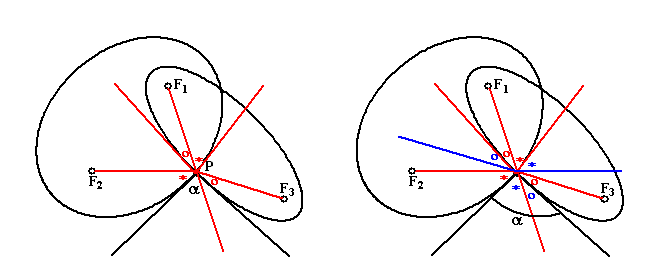
| In de
linkerfiguur zijn die raaklijnen rood getekend. De hoeken met een
*
(van de linkerellips) zijn aan elkaar gelijk en ook de hoeken met een
o
(van de rechterellips) In de rechterfiguur zijn de raaklijnen doorgetrokken. Overstaande hoeken zijn gelijk en dat levert ons de blauwe * en o. Nu is eenvoudig te zien dat α = o* en F2PF3 = oo** dus dat is het dubbele. |
|||||
| 8. | uit
de raaklijneigenschap van ellipsen weet je dat ∠PAF1
= ∠SAF2 de figuur is symmetrisch in de lijn PR en als je hoek ∠BF1 daarin spiegelt krijg je ∠SAF2 dus geldt ∠QBF1 = ∠SAF2 = ∠PAF1 |
||||
| 9. |
|
||||
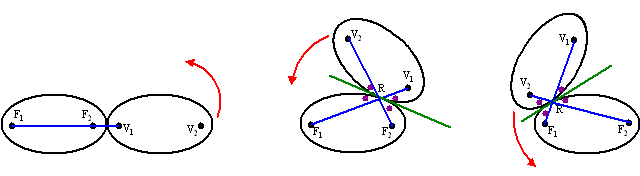
| Omdat de ellipsen
identiek zijn en langs elkaar rollen is de gerolde afstand (groen
hiernaast) gelijk, dus R het zelfde punt op beide ellipsen. De
figuur is symmetrisch tov de raaklijn. Maar omdat de hoeken met de raaklijn voor een ellips gelijk zijn betekent dat, dat alle vier de paarse hoeken bij R gelijk zijn. Dus is V1F1 een rechte lijn (overstaande hoeken). V1F1 = RF1 + RF2 en dat is constant (ellipseigenschap) V1F1 is constant dus beschrijft V1 een cirkel met middelpunt F1 |
|||||
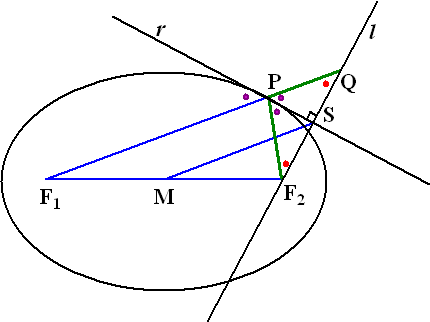
| 10a. | de hoeken met de
raaklijnen bij P zijn gelijk (ellipsegenschap0 Dan is ∠QPS daar ook aan gelijk (overstaande hoeken) Dan is driehoek QPF2 gelijkbenig met top P. Dus F2S = SQ MF1 = MF2 Dus MS is een middenparallel van driehoek F1F2Q Dus MS = 1/2F1Q = 1/2(F1P + PQ) Maar PQ = PF2 dus MS = 1/2(F1P + PF2) |
 |
|||
| 10b. | MS is constant (want
PF1 + PF2 is constant). Dus liggen de punten S op een cirkel met middelpunt M |
||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||