|
|||||
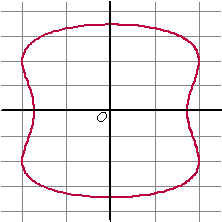
| 1 | a. | y4 + 16x2
= 48 + 8y2 snijpunt x-as: 16x2 = 48 ⇒ x2 = 3 ⇒ x = ±√3 dus de punten (√3, 0) en (-√3, 0) snijpunt y-as: y4 = 48 + 8y2 y4 - 8y2 - 48 = 0 (y2 - 12)(y2 + 4) = 0 y2 = 12 ∨ y2 = -4 y = ±√12 dus de punten (0, √12) en (0, -√12) 4y3dy + 32xdx = 16ydy 32xdx = dy(16y - 4y3) dy/dx = 32x/(16y - 4y³) evenwijdig aan de x-as: 32x = 0 ⇒ x = 0 en dat geeft de punten (0, √12) en (0, -√12) zie boven. evenwijdig aan de y-as: 16y - 4y3 = 0 4y(4 - y2) = 0 y = 0 ∨ y = 2 ∨ y = -2 y = 0 geeft de punten (√3, 0) en (-√3, 0) (zie boven) y = 2 geeft 16 + 16x2 = 48 + 32 ⇒ 16x2 = 64 ⇒ x = ±2 y =-2 geeft precies hetzelfde: x = ±2 Dat zijn dus de punten (2, 2)(-2, 2)(2, -2)(-2, -2) delen door y4 : 1 + 16x2/y2 = 48/y4 + 8/y2 voor y naar oneindig geeft dat geen horizontale asymptoot
delen door x2:
y4/x2 + 16 = 48/x2
+ 8 |
 |
||
| b. | y = x
geeft: y4 + 16y2
= p + 8y2 y4 + 8y2 - p = 0 y2 kun je nu met de ABC-formule uitrekenen: y2 = (-8 ±√(64 + 4p))/2 Dat geeft de volgende mogelijkheden: y2 = 0 als -8 + √(64 + 4p) = 0 ⇒ p = 0 en dan is er ιιn oplossing voor y dus q = 1 y2 > 0 als √(64 + 4p) > 8 ⇒ p > 0 en dan zijn er twee oplossingen voor y dus q = 2 y2 < 0 als √(64 + 4p) < 8 ⇒ p < 0 en dan zijn er geen oplossingen voor y (als p < -16 zijn er zelfs niet eens oplossingen voor y2) dus q = 0 |
||||
| c. | De maximale y
vind je als de helling 0 is: 32x = 0 ⇒ x = 0 (zie boven) en dat geeft y4 = p + 8y2 als y = ±9, dan geeft dat 6561 = p + 648 ⇒ p = 5913 De maximale x vind je als de helling ∞ is: 16y - 4y3 = 0 ⇒ 4y(4 - y2) = 0 ⇒ y = 0 ∨ y = 2 ∨ y = -2 y = 0 geeft 16x2 = 5913 ⇒ x2 = 369,5625 y = ±2 geeft 16 + 16x2 = 5913 + 32 ⇒ x2 = 370,5625 Die laatsten geven de grootste waarden voor x: bereik [-√370.5625, √370.5625] |
||||
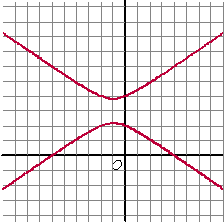
| 2. | a. | x2 - 3y2 +
2x
+ 18y - 24 = 0 x = 0 -3y2 + 18y - 24 = 0 y2 - 6y + 8 = 0 (y - 4)(y - 2) = 0 y = 4 ∨ y = 2 en dat zijn de snijpunten (0, 2) en (0, 4) y = 0 x2 + 2x - 24 = 0 en dat heeft geen oplossingen. (x - 4)(x + 6) = 0 x = 4 ∨ x = -6 en dat zijn de snijpunten (4, 0) en (-6, 0) 2xdx - 6ydy + 2dx + 18dy = 0 dx(2x + 2) = dy(6y - 18) dy/dx = (2x + 2)/(6y - 18) evenwijdig aan de x-as: 2x + 2 = 0 ⇒ x = -1 1 - 3y2 - 2 + 18y - 24 = 0 -3y2 + 18y - 25 = 0 y = (-18 ±√(324 - 300))/-6 ≈ 3,81 of 2,18 dus (-1, 3.81) en (-1, 2.18) evenwijdig aan de y-as: 6y - 18 = 0 ⇒ y = 3 x2 - 27 + 2x + 54 - 24 = 0 x2 + 2x + 3 = 0 en dat heeft geen oplossingen x2 - 3y2 + 2x + 18y - 24 = 0 delen door x2: 1 - 3y²/x² + 2/x + 18y/x² - 24/x² = 0 dat geeft geen horizontale asymptoten als x naar oneindig gaat. maar wel 1 - 3(y/x)2 = 0 ⇒ y/x = ±√(1/3) dus er zullen scheve asymptoten met helling ±√(1/3) zijn Die hebben vergelijking y = √(1/3)x + b en y = -√(1/3)x + b |
 |
||
| invullen: x2
- 3(√(1/3)x
+ b)2 + 2x + 18(√(1/3)x
+ b) - 24 = 0 x2 - x2 - 2√(1/3)xb - 3b2 + 2x + 6√3x + 18b - 24 = 0 Deel alles door x: -2√(1/3)b - 3b2/x + 2 + 6√3 + 18b/x - 24/x2 = 0 Als x naar oneindig gaat geeft dat -2/3√3b + 2 + 6√3 = 0 -2b + 2√3 + 18 = 0 b = √3 + 9 |
|||||
| b. | punt (-1 + a,
3 + b): (-1 + a)2 - 3(3 + b)2 + 2(-1 + a) + 18(3 + b) - 24 = 0 1 - 2a + a2 - 27 - 18b - 3b2 - 2 + 2a + 54 + 18b - 24 = 0 a2 - 3b2 + 2 = 0 punt (-1 - a, 3 - b): (-1 - a)2 - 3(3 - b)2 + 2(-1 - a) + 18(3 - b) - 24 = 0 1 + 2a + a2 - 27 + 18b - 3b2 - 2 - 2a + 54 - 18b - 24 = 0 a2 - 3b2 + 2 = 0 Dat geeft dezelfde vergelijking, dus de kromme is symmetrisch ten opzichte van (-1, 3) |
||||
| c. | x2 - 3y2 + px
+ 18y - 24 = 0 2xdx - 6ydy + pdx + 18dy = 0 dx(2x + p) = dy(6y - 18) dy/dx = (2x + p)/(6y - 18) snijpunten met de y-as: x = 0 - 3y2 + 18y - 24 = 0 en dat zijn de punten (0, 2) en (0, 4) in (0, 2) is de helling p/-6 in (0, 4) is de helling p/6 die staan loodrecht op elkaar als p/-6 p/6 = -1 p2 = 36 p = ±6 |
||||
| 3. | a. | (x2 + y2 - 2x)2
= 4(x2 + y2) x = 0 y4 = 4y2 y2 (y2 - 4) = 0 y = 0 ∨ y = 2 ∨ y = -2 en de snijpunten zijn (0, 0) en (0, 2) en (0, -2) y = 0 (x2 - 2x)2 = 4x2 x4 - 4x3 + 4x2 = 4x2 x3(x - 4) = 0 x = 0 ∨ x = 4 en de snijpunten zijn (0,0) en (4,0) |
|||
| b. | (x2 + y2 - 2x)2
= 4(x2 + y2) 2(x2 + y2 - 2x) (2xdx + 2ydy - 2dx) = 8xdx + 8ydy de snijpunten met de y-as zijn (0, 2) en (0, -2) dat geeft in (0, 2): 2 4 (4dy - 2dx) = 16dy 32dy - 16dx = 16dy en dat geeft dy/dx = 1 dat geeft in (0, -2): 2 4 (-4dy - 2dx) = -16dy -32dy - 16dx = -16dy en dat geeft dy/dx = -1 |
||||
| 4. | a. | (x2 + y2)2
- 4(x2 - y2) + 1 = 0
x = 0 y4 + 4y2 + 1 = 0 y2 = (-4 ±√(16 - 4))/2 = -2 ± √3 maar die zijn beiden negatief, dus dat geeft geen oplossingen. y = 0 x4 - 4x2 + 1 = 0 x2 = (4 ±√(16 - 4))/2 = 2 ± √3 x = √(2 ± √3) dat geeft 4 snijpunten: (√(2 + √3), 0) (√(2 - √3), 0) (-√(2 + √3), 0) (-√(2 -√3), 0) |
|||
| b. | y = p
heeft precies twee snijpunten op de plaatsen waar de helling nul is. (x2 + y2)2 - 4(x2 - y2) + 1 = 0 x4 + 2x2y2 + y4 - 4x2 - 4y2 + 1 = 0 4x3dx + 4xy2dx + 4yx2 dy + 4y3dy - 8xdx - 8ydy = 0 dx(4x3 + 4xy2 - 8x) = dy(8y - 4yx2 - 4y3) de helling is nul als 4x3 + 4xy2 - 8x = 0 4x(x2 + y2 - 2) = 0 x = 0 ∨ x2 + y2 = 2 x = 0 heeft geen oplossing (zie vraag a) x2 + y2 = 2 geeft x2 = 2 - y2 en dat kun je invullen in de vergelijking van K: 4 - 4(2 - 2y2) + 1 = 0 4 - 8 + 8y2 + 1 = 0 8y2 = 3 y = ±√(3/8) dus p = ±√(3/8) |
||||
| 5. | a. | y2 (1 - x2)
= (x2 + 2y - 1)2 x = 0 y2 = (2y - 1)2 y2 = 4y2 - 4y + 1 0 = 3y2 - 4y + 1 y = (4 ±√(16 - 12))/6 = 1 of 1/3 en dat zijn de snijpunten (0, 1) en (0, 1/3) y = 0 0 = (1 - x2)2 1 - x2 = 0 x = 1 ∨ x = -1 en dat zijn de snijpunten (1, 0) en (-1, 0) |
|||
| b. | de rechterkant is een
kwadraat, dus dat is altijd ≥ 0. dus moet de linkerkant ook ≥ 0 zijn. y2 is ook een kwadraat dus altijd 0 dus moet (1 - x2) ook ≥ 0 zijn dat is zo als x2 ≤ 1 dus als -1 ≤ x ≤ 1 |
||||
| 6. | a. | x3 + y3 = 3xy delen door x3 : 1 + (y/x)3 = 3y/x² als y en x beiden naar oneindig gaan, dan gaat de rechterkant naar 0 dat geeft (y/x)3 = -1 (y/x) = -1 de helling van de scheve asymptoot is -1 dus de scheve asymptoot heeft de vorm y = -x + b dat geeft x3 + (-x + b)3 = 3x(-x + b) x3 - x3 + 3x2b - 3xb2 + b3 = -3x2 + 3xb deel alles door x2: 3b - 3b²/x + b³/x² = -3 + 3b/x Als x naar oneindig gaat geeft dat 3b = -3 dus b = -1 de scheve asymptoot is y = -x - 1 |
|||
| b. | Vul het punt (y,
x) in: y3 + x3 =
3yx dat is de zelfde vergelijking als de oorspronkelijke, dus de kromme is symmetrisch in y = x |
||||
| c. | x3 + y3 = 3xy 3x2dx + 3y2dy = 3ydx + 3xdy dx(3x2 - 3y) = dy(3x - 3y2) de raaklijn is evenwijdig aan de x-as als 3x2 - 3y = 0 dat geeft y = x2 invullen: x3 + x6 = 3x3 0 = x3 (2 - x3) x = 0 ∨ x = 21/3 dat zijn de punten (0,0) en (21/3, 22/3) de raaklijn is evenwijdig aan de y-as als 3x - 3y2 = 0 dat geeft x = y2 invullen: y6 + y3 = 3y3 y3 (x3 - 2) = 0 y = 0 ∨ y = 21/3 dat zijn de punten (0,0) en (22/3, 21/3) |
||||
| 7. | a. | (x + 1)(x2 + y2)
= 4x2 y = 0: (x + 1)x2 = 4x2 x3 + x2 - 4x2 = 0 x2(x - 3) = 0 x = 0 ∨ x = 3 dus de snijpunten zijn (0,0) en (3,0) |
|||
| b. | (x + 1)(x2 + y2)
= 4x2 x3 + xy2 + x2 + y2 = 4x2 deel alles door y2: x³/y² + x + x²/y² + 1 = 4x²/y² als y naar oneindig gaat staat er x + 1 = 0 de verticale asymptoot is de lijn x = -1 |
||||
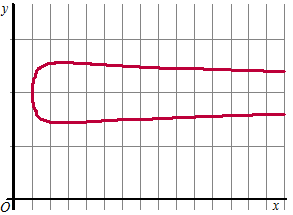
| 8. | a. | 2lnx = x(y -
2)2 Dat x > 0 kun je al wel zien aan de logaritme lnx want die bestaat anders niet. 2lnx/x = (y - 2)2 Omdat (y - 2)2 altijd positief moet zijn, moet lnx/x ook altijd positief zijn (anders bestaat y niet) Maar tussen 0 en 1 is x positief, en lnx negatief, dus het quotiλnt van die twee negatief. Daarom kan x ook geen waarden tussen 0 en 1 aannemen. |
 |
||
| b. | Vul voor y
2 + p in, dan staat er 2lnx = x(2 + p
- 2)2 ⇒ 2lnx = p2x Vul voor y 2 - p in, dan staat er 2lnx = x(2 - p - 2)2 ⇒ 2lnx = (-p)2x = p2x Dat is dezelfde vergelijking, dus dat geeft ook dezelfde x-waarden |
||||
| c. | 2 1/x
dx = 1 (y - 2)2 dx + x 2 (y
- 2)dy dx (2/x - (y - 2)2 ) = dy (2x(y - 2)) De raaklijn is verticaal als 2x(y - 2) = 0 en 2/x - (y - 2)2 Ή 0 Dat si zo als x = 0 ∨ y = 2 x = 0 vervalt (zie vraag a) y = 2 geeft 2lnx = 0 dus x = 1 en het punt (1,2) De raaklijn is horizontaal als 2/x - (y - 2)2 = 0 (y - 2)2 = 2/x en dat kun je invullen in de vergelijking: 2lnx = x 2/x 2lnx = 2 x = e (y - 2)2 = 2/e ⇒ y = 2 ±√(2/e) en dat zijn de punten (e, 2 ±√(2/e) ) ongeveer (2.72, 2.86) en (2.72, 1.14) |
||||
| 9. | a. | y4
- 4y2 = x4 - 6x2
4y3dy - 8ydy = 4x3dx - 12xdx dy(4y3 - 8y) = dx(4x3 - 12x) dy/dx = (4x³ - 12x)/(4y³ - 8y) x = √6 en y = 2 geeft dan dy/dx = 12√6/16 = 3/4√6 De raaklijn is y = 3/4√6x + b en gaat door (√6, 2) 2 = 3/4√6 √6 + b ⇒ b = -21/2 De raaklijn is y = 3/4√6 x - 21/2 |
|||
| b. | x = 4:
y2 (y2 - 4) = 160 (y2)2 - 4y2 - 160 = 0 y2 = (4 ±√656)/2 = 2 ±√164 omdat y2 positief is geldt alleen y2 = 2 + √164 dan is y = ±√(2 + √164) De afstand daartussen is 2√(2 + √164) |
||||
| c. | zie a) voor de
afgeleide evenwijdig aan de y-as betekent 4y3 - 8y = 0 4y(y2 - 2) = 0 y = 0 ∨ y = √2 ∨ y = -√2 y = 0 geeft x = 0 ∨ x = ±√6 maar bij x = 0 is ook 4x3 - 12x = 0 dus dan is de helling 0/0. Blijft over de punten (√6, 0) en (-√6, 0) y = ±√2 geeft x2(x2 - 6) = -4 (x2)2 - 6x2 + 4 = 0 ABC-formule: x2 = (6 ±√20)/2 = 3 ±√5 Dat geeft 4 mogelijkheden: x = ±√(3 ±√5) Dat geeft de punten (±√(3 ±√5), ±√2) dus dat zijn maar liefst 8 punten! In totaal 10 oplossingen: (√6, 0) (-√6, 0) (√(3 +√5), √2) (√(3 -√5), √2) (-√(3 +√5), √2) (-√(3 -√5), √2) (√(3 +√5), -√2) (√(3 -√5), -√2) (-√(3 +√5), -√2) (-√(3 -√5), -√2) |
||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||