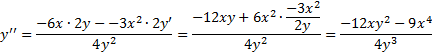© h.hofstede (h.hofstede@hogeland.nl)

       
1. a. x2 + y2 = px
2xdx + 2ydy = pdx
2ydy = pdx - 2xdx
dy/dx = (p - 2x)/2y     .....(1)

x2 + y2 = qy
2xdx + 2ydy = qdy
2xdx = qdy - 2ydy
dy/dx = 2x/(q - 2y)     .... (2) 

Als twee krommen elkaar snijden, dan geldt  x2 + y2 = px   en  x2 + y2 = qy dus dan is  px = qy
Vermenigvuldig (1) en (2) met elkaar en gebruik deze laatste vergelijking:
(p - 2x)/2y  • 2x/(q - 2y)
= (2px - 4x²)/(2qy - 4y²)
=  (2qy - 4x²)/(2qy - 4y²)

maar  x2 + y2 = qy  dus  x2 = qy - y2   en dan kun je die 2x2 vervangen:

=   (2qy - 4qy + 4y²)/(2qy - 4y²)
=    (-2qy + 4y²)/(2qy - 4y²)
= -1

Dat is inderdaad loodrecht.
       
  b. y = px3  
dy = 3px2 dx
dy/dx = 3px2

x2 + 3y2 = q
2xdx + 6ydy = 0
dy/dx = -2x/6y = -x/3y

y = px3 

vermenigvuldig weer beide hellingen met elkaar en gebruik dan dat y = px3  :

3px2  • -x/3y
=  -3px³/3y
=  - px³/y 
=  -y/y
= -1

Inderdaad loodrecht.
       
  c. snijpunt:  4a(a - x) = 4b(x + b)
a2 - ax = bx + b2
a2 - b2 = x(b + a)
(a - b)(a + b) = x(a + b)
x = a - b   ∨  a + b = 0
x = a - b geeft  y2 = 4a(a - a + b) = 4ab   .....(1)
(a + b = 0 geeft  b = -a en dan vallen de krommen samen. en dat viel af)

hellingen:
eerste:  2ydy = -4adx  geeft  dy/dx = -4a/2y = -2a/y
tweede:  2ydy = 4bdx  geeft  dy/dx = 4b/2y = 2b/y
vermenigvuldig de hellingen met elkaar:   -2a/y • 2b/y = -4ab/y2 
maar (1) zegt dat y2 = 4ab  dus de hellingen met elkaar vermenigvuldigd levert  -1 op.
Dat is loodrecht.
       
2. a. 6x2 - 4y2 = x

12xdx - 8ydy = dx
8ydy = 12xdx - dx
dy/dx = (12x - 1)/8y = y'

en nu nog een keer differentiëren, met de quotiëntregel:
   

       
  b. x3 + y2 = 0

3x2dx + 2ydy = 0
dy/dx = -3x²/2y  =  y'

en nu nog een keer met de quotiëntregel:
   

       
3. Stel de hoogte h
Dan heeft de getekende lichtstraal helling  h/21
De vergelijking ervan is  y = h/21 • x + 9h/21  (want gaat door (-9, 0))
Omdat die straal de ellips raakt, heeft de ellips in het raakpunt ook helling h/21.

x2 + 4y2 = 36
2xdx + 8ydy = 0
dy/dx = -2x/8y = -x/4y

Dus voor het raakpunt geldt:   - x/4y = h/21  en    y = h/21 • x + 9h/21   en  x2 + 4y2 = 36
De eerste geeft  x = -4yh/21  en dat kun je invullen in de tweede:

y = -4yh²/441 + 9h/21
y(1 + 4h²/441) = 9h/21
y (441 + 4h²)/441 = 9h/21
y =  (9h • 441)/(21(441 + 4h²))

Tijd voor de GR.
noem h = X
Y1 = (9X•441)/(21(441 + 4X^2))   is dan y
Y2 = -4Y1•X/21   is dan x
Y3 = Y2^2 + 4I1^2
Y4 = 36
intersect Y3 en Y4 geeft  h = 9,39   (raakpunt  ( -4.00 , 2.24))

Overigens kreeg ik heel terecht van Douwe Persijn de opmerking dat het ook best zonder rekenmachine kan, en exact. Kijk maar:
x2 + 4y2 = 36  geeft  dy/dx = -x/4y
de raaklijn y = ax + b door  (-9,0) geeft  y = a(x + 9) dus  a = y/(x + 9)
a = dy/dx  geeft dan   y/(x + 9) = -x/4y  en dat geeft  4y2 = -x2 - 9x
invullen in de ellipsvergelijking geeft x2 + (-x2 - 9x) = 36  dus  x = -4
 y/(x + 9) = -x/4y levert dan  y = √5
Het raakpunt is  (-4, √5) en invullen in de raaklijnvergelijking geeft a = 1/5√5
De raaklijn is de lijn  y = 1/5√5 • x + 9/5√5
x = 12 geeft dan  y = h = 21/5√5
       

© h.hofstede (h.hofstede@hogeland.nl)