© h.hofstede (h.hofstede@hogeland.nl)

       
1. a. x ' = 2cos(t)
y ' = 2cos(2t)
v(3) = √( (2cos3)2 + (2cos6)2) = 2,76
       
  b. v(t) = √(4cos2t + 4cos22t) = 2√(cos2t + cos22t)
Dat is maximaal als wat onder die wortel staat maximaal is, en dan is de afgeleide daarvan nul:
-2costsint - 4cos2tsin2t = 0
sin2t + 2cos2tsin2t = 0
sin2t(1 + 2cos2t) = 0
sin2t = 0  ∨ 1 + 2cos2t = 0
sin2t = 0 ∨  cos2t = -1/2
2t = 0 ∨ 2t = π  ∨  2t = 2/3π  ∨  2t = 11/3π   (alles + k2π)
t =  0,  π, 1/2π,   11/2π,   1/3π,  2/3π,  11/3π,  12/3π
Dat geeft respectievelijk:    cos2t + cos22t =  2,  2,  1,  1, 1/2,  1/2,   1/2,  1/2
De maximale snelheid is dus  2√2
       
2. a. In het hoogste punt is  y ' = 0
y ' = 4t - t2 = t(4 - t) = 0
dat is voor t = 0  ∨  t = 4
t = 0 geeft het punt  (0,0)
t = 4 geeft het punt (8, 102/3) en dat is het hoogste punt.
       
  b. x ' = 6 - 2t  dus  x '(2) = 2
y ' = 4t - t2  dus  y'(2) = 4
v(2) = √(22 + 42) = √20
       
  c. v = √((6 - 2t)2 + (4t - t2)2 )
voer deze formule in bij Y1 in de GR en gebruik calc - maximum
Dat geeft maximale snelheid 1,77  (bij t = 3,77)
       
3. a. x = (cost)-1  dus x' = -(cost)-2• -sint  en  x '(1/3π) = 2√3
y = tant  dus  y '= 1/(cos2t)  en  y '(1/3π) = 4
Dan is  v(1/3π) = √((2√3)2 + 42) = √28
       
  b. x' 2 = sin²t/cos4t 
y' 2 = 1/cos4t
x' 2  + y ' 2 = 2  geeft dan  sin²t/cos4t  + 1/cos4t = 2
sin2t + 1 = 2cos4t
1 - cos2t + 1 = 2cos4t
2cos4t + cos2t - 2 = 0
(cos2t - 1)(cos2t + 2) = 0
cos2t = 1 ∨ cos2t  = -2  (maar dat laatste kan niet)
cost = 1  ∨ cost = -1
t = 0  ∨  t = π
Dat geeft de punten  (1, 0)  en (-1, 0)
       
4. a. De x-snelheid is constant, dus de totale snelheid is minimaal als de y-snelheid minimaal is. Dat is in de top want daar is de y-snelheid 0.
       
  b. x ' = 1
y = (1 + t2)-1  dus  y ' = -(1 + t2)-2 • 2t  en dan is  y '(1/2) = -0,64
v(1/2) = √(1 + 0,4096) = 1,19
       
  c. v = √( 1 + 4t² / (1 + t² )4 )
Voer deze formule in bij Y1 van de GR en gebruik calc - maximum.
Dat geeft maximale snelheid 1,192  (bij t = ±0,577)
       
5. y = 9,8
5t - 0,625t2 = 9,8
0,625t2 - 5t + 9,8 = 0
t = (5 ±√(25 - 24,5))/1,25 = 3,434  of  4,567
Dat is voor het eerst bij t = 3,434

x ' = 7,5
y ' =  5 - 1,25t dus  y '(3,434) = 5 - 1,25 • 3,434 = 0,7075
v(3,434) = √(7,52 + 0,70752) = 7,53  m/s
       
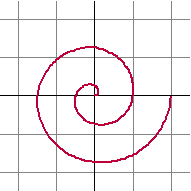
6a. zie de plot hiernaast

x = 0
0,5 • t • cos(πt)  = 0
t = 0  cos(πt) = 0
t = 0  ∨  πt = 1/2π + kπ
t = 0, 1/2, 11/2, 21/2, 31/2
Dat geeft  y = 0, 1/4, -3/4, 11/4, -13/4
De positieve y-as is bij  y = 1/4 en y = 11/4 en de afstand daartussen is 1. 

       
6b. x(t) = 0,5 • t • cos(πt)
x ' = 0,5cos(πt) - 0,5tsin(πt) • π   dus  x '(2) = 0,5

y(t) = 0,5 • t • sin(πt)
y '  = 0,5 sinπt + 0,5t cos(πt) • π  dus  y '(2) =  π

v(2) = √(0,52 + π2) ≈  3,18
       
6c. Als je t vervangt door -t dan wordt x tegenovergesteld  (cos blijft gelijk, maar t draait om)  en y blijft gelijk (sin en t worden beiden tegengesteld, en dat heft elkaar op)
Als x tegengesteld wordt, en y blijft gelijk, dan wordt de kromme gespiegeld in de y -as.
       
7. a. x(t) = -t2 + 2t    dus  x(0) = 0
x ' = -2t + 2   dus  x '(0) = 2

y(t) = t2 - 4t + 3  dus  y(0) = 3
y ' = 2t - 4  dus  y '(0) = -4

De helling bij t = 0 is gelijk aan  -4/2 = -2  dus de raaklijn zal y = -2x + b zijn
Die moet door (0, 3) geen dus de vergelijking is  y = -2x + 3
       
  b. v = √((-2t + 2)2 + (2t - 4)2 )
Die is minimaal als dat deel onder de wortel minimaal is.
(-2t + 2)2 + (2t - 4)2  =  4t2 - 8t + 4 + 4t2 - 16t + 16  =  8t2 - 24t + 20   moet minimaal zijn
Dan is de afgeleide ervan nul:
16t - 24 = 0
t = 1,5
v(1,5) = √((-1)2 + (-1)2) = √2
       
  c. y = x + 11  geeft:
t2 - 4t + 3   = -t2 + 2t + 11
2t2 - 6t - 8 = 0
t2 - 3t - 4 = 0
(t - 4)(t + 1) = 0
t = 4 ∨ t = -1

t = 4  geeft het punt  (-8, 3)
t = -1 geeft het punt  (-3, 8)
De afstand daartussen is  √(52 + 52) = √50 = 2√5
       
8. x ' (t) = -15sin(15t)- 2sin(2t) dus x'(0) = 0
y ' (t) = 15cos(15t) + 2cos(2t) dus y '(0) = 17
De snelheid is √(x'2 + y'2) = √172 = 17
       
9. a. x = 0
cos3t = 0
3t = 1/2π + k2π  ∨  3t = 11/2π + k2π
t = 1/6π + k2/3π  ∨  t = 1/2π + k2/3π
Dat geeft de oplossingen {1/6π, 1/2π, 5/26π, 7/6π, 11/2π, 11/6π}

Daarbij horen de punten
(0, 1/2) (0, 1) (0, 1/2) (0, -1/2) (0, -1) (0, -1/2)
Dus dat zijn de punten   (0, 1/2) (0, 1) (0, -1/2) en (0, -1)
       
  b. x ' = -3sin(3t)
y ' = cost

v = √(9sin2(3t) + cos2t)
Voer deze formule in bij Y1 in de GR

Dat geeft zes maxima, waarvan er twee liggen bij t = 1/2π en t = 11/2π, dus waar de grafiek de y-as snijdt.
Maar de maxima in deze twee toppen (v = 3)  zijn lager dan in de andere vier toppen  (v = 3,122)
Dus dat is NIET het geval.
       
10. a. y = 0  ⇒  sin(2t + 1/3π) = 0 
⇒  2t + 1/3π = 0  (mod 2π)  ∨  2t + 1/3π = π  (mod 2π)
⇒  2t = -1/3π (mod 2π)  ∨  2t = 2/3π (mod 2π)
⇒  t = -1/6π (mod π)  ∨  t = 1/3π (mod π)
Tussen 0 en 2π (de gemeenschappelijke periode) geeft dat de oplossingen:
 t = 1/3π , 5/6π , 4/3π en 11/6π
Dat levert de snijpunten  (1/2√3 , 0) en (-1/2 , 0) en (-1/2√3 , 0) en  (1/2 , 0) 
       
  b. x = 0  geeft  t = 0  ∨  t = π
De snelheid v  is  v = √((x')2 + (y')2) = √ (cos2t + 4 • cos2(2t + 1/3π))
t = 0 levert v = √((1)2 + 4 • (1/2)2) = √2
en t = p zal dan wel dezelfde snelheid leveren.
       
  c. A heeft y-coördinaat sin(2a + 1/3π) 

B heeft y- coördinaat  sin(2(π - a) + 1/3π)
= sin(2π - (2a - 1/3π))
= -sin(2a - 1/3π)

Het verschil daartussen is  sin(2a + 1/3π) - - sin(2a - 1/3π) = sin(2a + 1/3π) + sin(2a - 1/3π)

Uitschrijven met de somformules geeft:
AB = sin 2a • cos1/3π + cos 2a • sin 1/3π + sin 2a • cos 1/3π - cos 2a • sin 1/3π
= 1/2sin2a + 1/2sin2a
= sin 2a
       

© h.hofstede (h.hofstede@hogeland.nl)