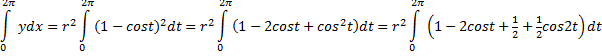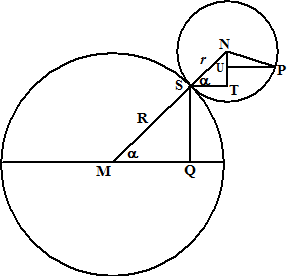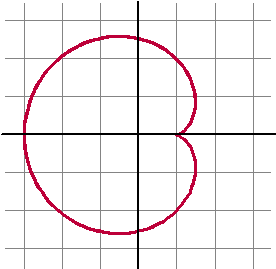|
|||||
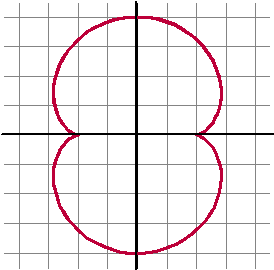
| 1. | a. | x' = 1 - cost y ' = sint Y1 = √((1 - cos(X))^2 + (sin(X))^2) calc - ∫f(x)dx voor X = 0 tot X = 2π geeft L = 8 |
|||
| b. | v2
= (1 - cost)2 + sin2t = 1 - 2cost + cos2t + sin2t = 1 - 2cost + 1 = 2 - 2cost dus v is daar de wortel van. |
||||
| c. | de afgeleide van -2√(1 + cost) = -2(1 + cost)0,5 is: | ||||
|
|
|||||
| De formule geldt
alleen tussen 0 en
π, omdat dan geldt
√(sin2t) = sint Tussen π en 2π zou gelden √(sin2t) = -sint en zou de primitieve een minteken krijgen. |
|||||
| d. |
|
||||
| =
√2 • {-2•0 - - 2•√2} = √2 • 2√2 = 4 De hele omtrek is dan 2 • 4 = 8 |
|||||
| 2. | x = rt
- rsint dus dx = (r - rcost)dt y = r - rcost |
||||
|
|
|||||
|
|
|||||
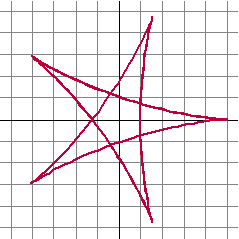
| 3. | a. | de periode van cosα
is 2π de periode van cos 11/2α is 2π/1,5 = 4/3π de gemeenschappelijke periode van 2π en 4/3π is 4π dus dat is de periode van x(α) voor y(α) geldt precies hetzelfde. |
|||
| b. | de kleine cirkel
geeft omtrek 4π, de grote heeft omtrek 10π de periode is 4π, dus daarin wordt de grote cirkel twee keer rondgedraaid dan maakt de kleine cirkel 5 omwentelingen (omtrek 4π gaat 5 keer in omtrek 20π) x'(α) = -3sinα - 2sin(11/2α)•11/2 = -3sinα - 3sin(11/2α) = 0 3sin(11/2α) = -3sinα = 3sin(-α) sin(11/2α) = sin(-α) 11/2α = -α + k2π ∨ 11/2α = π + α + k2π 21/2α = k2π ∨ 1/2α = π + k2π α = 0 + k2/5π ∨ α = 2π + k4π dat geeft α = 0, 2/5π, 4/5π, 6/5π, 8/5π |
||||
|
y'(α) = 3cosα
- 2cos(11/2α)•11/2
= 3cosα
- 3cos(11/2α)
= 0 cosα = cos(11/2α) α = 11/2α + k2π ∨ α = -11/2α + k2π -1/2α = k2π ∨ 21/2α = k2π α = k4π ∨ α = k2/5π dat geeft α = 0, 2/5π, 4/5π, 6/5π, 8/5π Die waarden geven (afgerond) de volgende keerpunten: (5, 0) en (0.31, 0.95) en (-4.05, 2.94) en (-0.81, -0.59) en (1.55, 4.76) |
|||||
| c. | hiernaast |
|
|||
| 4. | a. | Omdat die rode stukken gelijk
zijn is Rα = rβ dus β = R/r• α Neem M als oorsprong. xP = MQ + ST + PU MQ = Rcosα ST = rcosα ∠(PNU) = β - (90 - α) PU = rsinPNU = rsin(β - 90 + α) = rsin(R/r• α + α - 90) = - rcos(R/r• α + α) xP = Rcosα + rcosα - rcos(R/r• α + α) yP = SQ + TN - NU SQ = Rsinα NT = rsinα NU = rcosPNU = rcos(β - 90 + α) = rcos(R/r • α + α - 90) = rsin(R/r• α + α) yP = Rsinα + rsinα - rsin(R/r• α + α) |
|
||
| b. | Neem R = r = 1 Dan is x = 2cosα - cos(2α) en y = 2sinα - sin(2α) Zie de figuur hiernaast. |
|
|||
| c. | Neem r = 1 en R = 2 Dan is x = 3cosα - cos(3α) en y = 3sinα - sin(3α) zie de figuur hiernaast |
|
|||
| 5. | a. | x ' = -0,1π
• 8 • sin(0,1πt) - 0,4π
• 3 • sin(0,4πt) y ' = 0,1π • 8 • cos(0,1πt) + 0,4π • 3 • cos(0,4πt) Zet deze formules in Y1 en Y2 van de GR. Y3 = √(Y1^2 + Y2^2) geeft dan de snelheid. calc - maximum van Y3 geeft maximale snelheid v = 6,28 |
|||
| b. | Gebruik de Y3 uit de
vorige vraag. calc - ∫f(x)dx van X = 0 tot X = 20 geeft L = 84,1 |
||||
| c. |
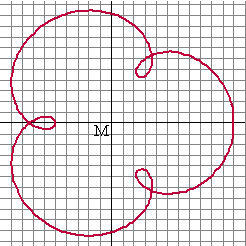 |
||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||