|
|||||
| 1. | a. | De afstand tot de oorsprong is 6,
dus dan geeft Pythagoras: x2 + y2
= 62 = 36 y2 = 36 - x2 en daaruit volgt direct de gegeven formule. |
|||
| b. | neem een strookje op hoogte h
met breedte 2x h = √(36 - x2) 36 - x2 = h2 x2 = 36 - h2 x = √(36 - h2) |
||||
|
|
|||||
| de oppervlakte is
1/2πr2
= 18p Als de hoogte van het zwaartepunt H is, dan geldt: 18π H = 144 H = 144/18π = 8/π = 2,546 |
|||||
| 2. | neem een strookje op
hoogte h met breedte 2x h = √x ⇒ x = h2 |
||||
|
|
|||||
|
|
|||||
| Noem de hoogte van
het zwaartepunt H, dan geldt: 16/3 H = 8 H = 24/16 = 1,5 |
|||||
| 3. | a. | Lijn AB heeft vergelijking y
= 3 - x dus h = 3 - x De oppervlakte van driehoek OAB is 4,5. |
|||
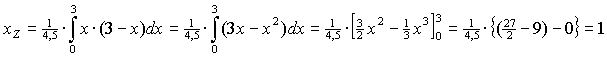 |
|||||
| En dus ook yZ = 1 | |||||
| b. | Je kunt de oppervlakte verdelen in
een rechthoek van 1 (breedte) bij 3 (hoogte) + een deel onder de
grafiek van y = 3/x. De rechthoek heeft oppervlakte 3. De hele oppervlakte is dus gelijk aan: |
||||
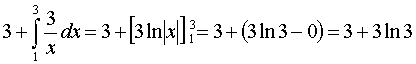 |
|||||
| Verder geldt: | |||||
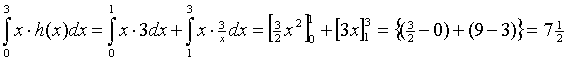 |
|||||
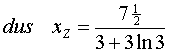 |
|||||
| 4. | Noem de totale hoogte
H en de straal van het grondvlak R (H - h)/r = H/R rH = R(H - h) = RH - Rh r = R - R/H h |
||||
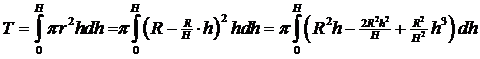 |
|||||
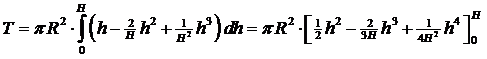 |
|||||
| T =
πR2 {1/2H2
- 2/3H2
+ 1/4H2} T = πR2 1/12H2 |
|||||
| De inhoud is
1/3πR2H
dus als Z de hoogte van het zwaartepunt is, moet gelden: 1/3πR2H Z = πR2 1/12H2 Z = 1/4H |
|||||
| 5. | h2 + r2 = 36 geeft r2 = 36 - h2 | ||||
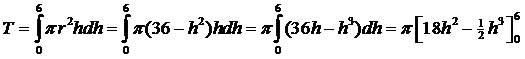 |
|||||
| = π (648 - 108) = 540π. | |||||
| De inhoud van een
halve bol met straal 6 is I = 2/3π
63 = 144π Als de hoogte van het zwaartepunt Z is, dan geldt: 144π Z = 540π Z = 3,75 |
|||||
| 6a. | één zo'n ringetje
heeft oppervlakte (en dus massa) 2πrdh
want dat is de omtrek van een cirkel met straal r en hoogte dh h = √(r - 4) ⇒ r - 4 = h2 ⇒ r = 4 + h2 Bij x = 8 is y = √(8 - 4) = 2 dus h loopt van 0 tot 2. |
||||
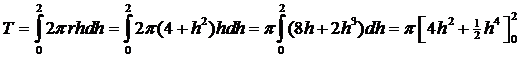 |
|||||
| T =
π (16 + 8) = 24π De totale oppervlakte O berekenen we ook met een integraal: |
|||||
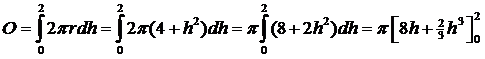 |
|||||
| O =
π (16 + 16/3) = 211/3π Als de hoogte van het zwaartepunt Z is, moet gelden 211/3π Z = 24π Z = 1,125 |
|||||
| 6b. |
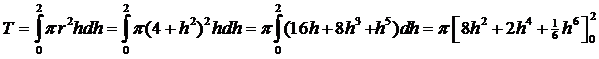 |
||||
| T =
π (32 + 32 + 102/3)
= 742/3π De inhoud I doen we ook met een integraal: |
|||||
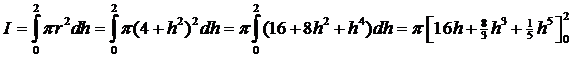 |
|||||
| I =
π (32 + 64/3 +
32/5) = 896/15π Als de hoogte van het zwaartepunt Z is, moet gelden 896/15π Z = 742/3π Z = 1,25 |
|||||
| 7. | V = 1/2 4/3 π 13 = 2/3π. | ||||
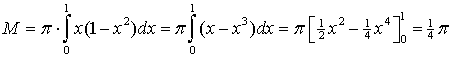 |
|||||
| xZ = M/V = 3/8 | |||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||