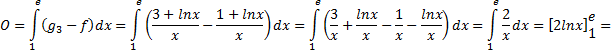|
|||||
| 1. | a. | f(x) = 4/(x +
3) F(x) = 4ln|x + 3| |
|||
| b. | f(x) = x + 2/x F(x) = 1/2x2 + 2ln|x| |
||||
| c. | f(x) = 1/(4x) F(x) = ln|4x| 1/4 |
||||
| d. | f(x) = 1/(3 - x)
F(x) = ln|3 - x| -1 = -ln|3 - x| |
||||
| e. | f(x) = 2/(3x
+ 1) F(x) = 2ln|3x + 1| 1/3 = 2/3ln|3x + 1| |
||||
| f. | f(x) = 1/(x2)
= x-2 F(x) = -x-1 = -1/x |
||||
| 2. | a. |
|
|||
| F(x) = x + 8ln|3x - 2| 1/3 = x + 8/3ln|3x - 2| | |||||
| b. |
|
||||
| F(x) = ln|x + 3| maar voor x = 2 bestaat de functie niet. | |||||
| c. |
|
||||
| F(x) = 2x - 13ln|x + 4| | |||||
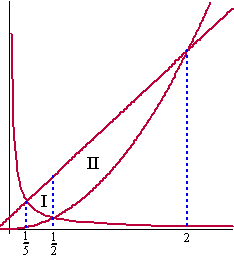
| 3. | snijpunten: 4x2 = 7,5x + 1 4x2 - 7,5x - 1 = 0 ABC-formule: x = (7,5 ±√(56,25 + 16))/8 = 2 of -1/8 4x2 = 1/2x 8x3 = 1 x3 = 1/8 x = 1/2 1/2x = 7,5x + 1 1 = 15x2 + 2x 15x2 + 2x - 1 = 0 ABC-formule: x = (-2 ±√(4 + 60))/30 = 1/5 of -1/3 |
|
|||
| Verdeel het gebied in twee stukken: I en II (zie de figuur) | |||||
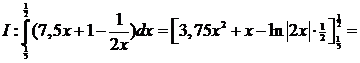 |
|||||
| = (0,9375 + 0,5 - 0,5 ln1) - (0,15 + 0,2 - 0,5 ln0,4) = 1,4375 - 0,35 + 0,5ln0,4 = 1,0875 - 0,5ln0,4 | |||||
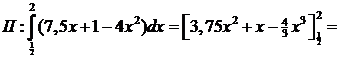 |
|||||
| = (15 + 2 - 102/3)
- (0,9375 + 0,5 - 1/6)
= 61/3
- 61/48
= 81/16 Samen is dat 6,15 - 0,5ln0,4 |
|||||
| 4. | Het is wél dezelfde
op een constante na: 1/2ln(2x) = 1/2(ln2 + lnx) = 1/2lnx + 1/2ln2 |
||||
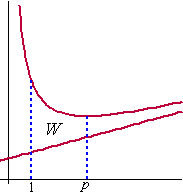
| 5. | a. | f(x) = 3,5 x2 + x + 1 = 3,5x x2 - 2,5x + 1 = 0 (x - 2)(x - 0,5) = 0 x = 2 ∨ x = 0,5 |
|||
| f(x) = x + 1 + 1/x | |||||
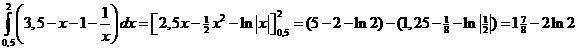 |
|||||
| b. |
|
|
|||
| lnp = 2 geeft dan p = e2 | |||||
| 6. | f(x) = 1 + 2/x + 2/x2 | ||||
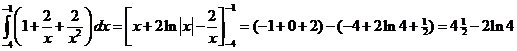 |
|||||
| 7. |
|
||||
| = 2lne - 2ln1 = 2 | |||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||