|
|||||
| 1. | f = g
geeft a + b√x = x2 - 8x
+ 16 en met x = 2 geeft dat a + b√2
= 4 f ' · g ' = -1 geeft b/2√x = 2x - 8 en met x = 2 geeft dat b/2√2 = -4 ⇒ b = -8√2 Dan wordt de bovenste vergelijking a + -8√2 · √2 = 4 a - 16 = 4 a = 20 |
||||
| 2. | x = 5 is
een verticale lijn en als die de grafiek loodrecht snijdt dan loopt de
grafiek in dat snijpunt horizontaal, dus is de helling nul. f(x) = (2x2 + px)e-x f ' = (4x + p)e-x + (2x2 + px)·-e-x = 0 x = 5 geeft dan e-5 (20 + p - 50 - 5p) = 0 20 + p - 50 - 5p = 0 -4p = 30 p = -71/2 |
||||
| 3. | f = g
geeft e-0,5x = p√x f ' · g' = -1 geeft -0,5e-0,5x · p/2√x = -1 e-0,5x is gelijk aan p√x dus dat kun je in die tweede formule daardoor vervangen: -0,5 · p√x · p/2√x = -1 -0,25p2 = -1 p2 = 4 p = 2 |
||||
| 4. | f = g
geeft 3sin3x = pcosx f ' · g' = -1 geeft 9sin2x cosx · -psinx = -1 De eerste vergelijking geeft p = 3sin3x/cosx invullen in de tweede, dan valt cosx weg: -9sin2x · 3sin3x · sinx = -1 sin6x = 1/27 sinx = (1/27)1/6 = (3-3)1/6 = 3-0,5 = 1/√3 = 1/3√3 dan is cosx = √(1 - sin2x) = √(1 - 1/3) = √(2/3) = 1/3√6 |
||||
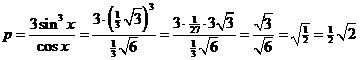 |
|||||
| 5. | a. | f1(x)
= x + √(1 - x) Randpunt als 1 - x = 0 ⇒ x = 1 ⇒ y = 1 dus punt (1,1) Top als f ' = 0 1 - 1/2√(1 - x) = 0 2√(1 - x) = 1 √(1 - x) = 1/2 1 - x = 1/4 x = 3/4 en dan is y = 3/4 + √1/4 = 3/4 + 1/2 = 5/4 dus top (1/4, 5/4) Snijpunt y-as: x = 0 dus y = 0 + √1 = 1 en punt (0, 1) |
|||
| b. | functies gelijk: x +
√(1 - px) = x +
√(1 - x) Daaruit volgt √(1 - px) = √(1 - x) 1 - px = 1 - x 0 = x(p - 1) x = 0 ∨ p = 1 Het gaat om de optie x = 0, want p = 1 geeft niet twee verschillende grafieken. f ' · g' = -1: (1 - p/2√(1 - px)) (1 - 1/2√(1 - x)) = -1 x = 0 invullen: (1 - p/2) (1 - 1/2) = -1 1/2(1 - 1/2p) = -1 1 - 1/2p = -2 1/2p = 3 p = 6 |
||||
| 6. | a. | f(x)
= 2x3 -
6x2 - 15x + 7 f ' = 6x2 - 12x - 15 6x2 - 12x - 15 = 3 6x2 - 12x - 18 = 0 x2 - 2x - 3 = 0 (x - 3)(x + 1) = 0 x = 3 ∨ x = -1 x = 3 geeft raakpunt y = 2 33 - 6 32 - 15 3 + 7 = -38 dus raakpunt (3, -38) -38 = 3 3 + b geeft b = -47 x = -1 geeft raakpunt y = 2 (-1)3 - 6 (-1)2 - 15 -1 + 7 = 14 dus raakpunt (-1, 14) 14 = 3 -1 + b geeft b = 17 De verticale afstand is dan 17 + 47 = 64 |
|||
| b. | De raaklijnen zijn y = 3x
- 47 en y = 3x + 17 Neem punt (0, 17) van de tweede raaklijn. Leg daar een lijn doorheen die er loodrecht op staat Die heeft dan hellinggetal -1/3, dus de vergelijking is y = -1/3x + 17 Snijden met de andere raaklijn: -1/3x + 17 = 3x - 47 64 = 31/3x x = 19,2 en dan is y = 10,6 Het gaat om de afstand tussen de punten (0, 17) en (19.2, 10.6) Pythagoras: A = √((19,2 - 0)2 + (10,6 - 17)2) = √409,6 ≈ 20,24 |
||||
| 7. | f ' = 2 e0,5x
dus f '(p) = 2 e0,5p
g ' = -0,5 e-0,5x dus g '(p) = -0,5 e-0,5p f ' g' = 2 e0,5p -0,5 e-0,5p = -1 dus dat is inderdaad loodrecht. |
||||
| 8. | Stel P = (p,
p2) OP heeft dan helling p De middelloodlijn heeft dan helling -1/p en gaat door (1/2p, 1/2p2) 1/2p2 = -1/p 1/2p + b geeft b = 1/2 + 1/2p2 De middelloodlijn is de lijn y = -1/p x + 1/2 + 1/2p2 Het snijpunt met de y-as is dan yQ = 1/2 + 1/2p2 Als P naar de oorsprong gaat, gaat p naar nul en wordt Q het punt (0, 1/2) |
||||
| 9. | Stel dat het raakpunt
R = (a, a2) is. De parabool heeft daar helling f ' (a) = 2a MR staat daar loodrecht op, dus MR heeft helling -1/2a Stel M = (0, h) dan is de helling van MR: (a² - h)/a = -1/2a Daaruit volgt a2 - h = -1/2 dus h = a2 + 1/2 MR2 = a2 + (a2 + 1/2 - a2)2 = 4 4 = a2 + 1/4 a2 = 15/4 M = (0, 17/4) |
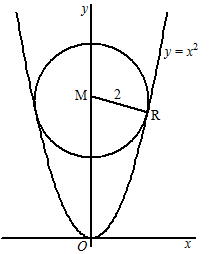 |
|||
| 10. | De verschoven grafiek heeft vergelijking
y = ln((x - 2)2 + 1) snijpunt: ln(x2 + 1) = ln((x - 2)2 + 1) x2 + 1 = (x - 2)2 + 1 x2 + 1 = x2 - 4x + 4 + 1 4x = 4 x = 1 oorspronkelijke afgeleide: f ' = 1/(x² + 1) 2x dus f '(1) = 1 verschoven afgeleide: f ' = 1/((x - 2)² 2(x - 2) dus f '(1) = -1 het product van de richtingscoλfficiλnten is -1 1 = -1 dus de grafieken snijden elkaar loodrecht. |
||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||