© h.hofstede (h.hofstede@hogeland.nl)

       
1. a. f(x) = 5x4 + 8x3 - 2x
f ' = 4 • 5x3 + 3 • 8x2 - 2 = 20x3 + 24x2 - 2
       
  b. f(x) = 4 - 3x3 + x2
f ' = 3 • -3x2 + 2 • x1  = -9x2 + 2x
       
  c. f(x) = 10x10 + 9x9 + 8x8
f ' =  10 • 10x9 + 9 • 9x8 + 8 • 8x7 = 100x9 + 81x8 + 64x7
       
  d. y = x + 6 - 8x4
y ' = 1 - 4 • 8x3  =  1 - 32x3
       
  e. f(x) = 5 + 14x + 1/2x8
f '  = 14 + 8 • 1/2x7 = 14 + 4x7
       
  f. y =  -0,4x3  - 2x4  + 10
y ' =  3 • -0,4x2 - 4 • 2x3 = -1,2x2 - 8x3
       
  g. y =  4 - 2x5 - 1/3x3
y'  = -5 • 2x4 - 3 • 1/3x2 = -10x4 - x2
       
  h. f(x) =  3x - 2x + 8x2 - 1
f ' = 3 - 2 + 2 • 8x1 = 1 + 16x
       
2. a. f(x) = 5x + 4 - 12x2
f ' = 5 - 2 • 12x1 = 5 - 24x
       
  b. f(x) = (2 - 3x) • (4x + 5) = 8x + 10 - 12x2 - 15x  = -7x + 10 - 12x2
f ' = -7 - 2 • 12x1 = -7 - 24x		  
       
  c. y = 2x2 • 3x4 = 6x6
y ' = 6 • 6x5 = 36x5		  
       
  d. f(x) = 3(2x2 + 8x5) = 6x2 + 24x5
f ' = 2 • 6x1 + 5 • 24x4 = 12x + 120x4 		 
       
  e. y = 6x - x • 3x2 = 6x - 3x3
y ' = 6 - 3 • 3x2 = 6 - 9x2		  
       
  f. f(x) = 40x - 30x2 • 2 = 40x - 60x2
f ' = 40 - 2 • 60x1 = 40 - 120x		  
       
  g. y = (40x - 30x2) • 2 = 80x - 60x2
y ' = 80 - 2 • 60x1 = 80 - 120x  		 
       
  h. f(x) = 3x3 - 2x2 • x + 5x = 3x3 - 2x3 + 5x  =  x3 + 5x
f ' = 3x2 + 5
       
3. a. f(x) = 3x6 - 2x
f ' = 6 • 3x5 - 2 = 18x5 - 2
f '(1) = 18 • 15 - 2 = 16  dus de raaklijn is  y = 16x + b
f(1) = 3 • 16 - 2 • 1 = 1  dus het raakpunt is (1,1)
1 = 16 • 1 + b ⇒  b = -15
de raaklijn is dan y = 16x - 15 
       
  b. f(x) = 3x6 - 2x
f ' = 6 • 3x5 - 2 = 18x5 - 2
f '(-0,8) = 18 • -0,85 - 2 = -5,89824  dus de raaklijn is  y = -5,89824x + b
f(-0,8) = 3 • (-0,8)6 - 2 • -0,8 = 2,386432  dus het raakpunt is (-0.8,2.386432)
2,386432 = -5,89824 • -0,8 + b ⇒  b = -2,33216
de raaklijn is dan y = -5,89824x - 2,33216 
       
4. a. h(0) = 50,4 - 4,9 • 02 + 0,5 • 03 = 50,4 meter  
       
  b. h' = -2 • 4,9t + 3 • 0,5t2 = -9,8t + 1,5t2 
h'(2) = -9,8 • 2 + 1,5 • 22 = -13,6 m/s
Het minteken betekent dat de kogel naar beneden valt.		  
       
  c.

Y1 = 50,4 - 4,9 • X2  + 0,5 • X3
calc - zero geeft  t = 4,269
h ' = -9,8t + 1,5t2   dus  h '(4,269) = -9,8 • 4,269 + 1,5 • 4,2692 = -14,5 m/sec

Y1 = 50,4 - 4,9 • X2 + 0,4 • X3
calc - zero  geeft  t = 3,880
h ' = -9,8t + 1,5t2   dus  h '(3,880) = -9,8 • 3,880 + 1,5 • 3,8802 = -15,4 m/sec

  
       
5. a. f(x) = 3x2 - 5x
f '(x) = 2 • 3x1 - 5 = 6x - 5
f '(3) = 6 • 3 - 5 = 13  dus de raaklijn is  y = 13x + b
f(3) = 3 • 32 - 5 • 3 = 12  dus het raakpunt is  (3, 12)
12 = 13 • 3 + b Þ  b = -27
De raaklijn is  y = 13x - 27
       
  b. f  ' = 8
6x - 5 = 8
6x = 13
x = 21/6.
y = 3 • (21/6)2 - 5 • 21/6 =  31/4
Dat is het punt  (21/6, 31/4)
       
  c. de lijn heeft helling 25, dus moet de grafiek dat ook hebben .
f ' = 25
6x - 5 = 25
6x = 30
x = 5
y = 3 • 52 - 5 • 5 = 50  dus de lijn moet door  (5, 50) gaan
50 = 25 • 5 + b  Þ b = -75  		 
       
6. a. De snelheid is de afgeleide.
s'(t) = 11 - 3 • 0,0000015t2  =  11 - 0,0000045t2
5 minuten is 300 seconden.
s' (300) = 11 - 0,0000045 • 3002 = 10,595  m/sec
       
  b. eind eerste rondje:  s = 400
Y1 = 11X - 0,0000015X^3 
Y2 = 400
intersect geeft  t = 36,37

eind tweede rondje:  s = 800
Y1 = 11X - 0,0000015X^3 
Y2 = 800
intersect geeft  t = 72,78 dus het tweede rondje duurde  72,78 - 36,37 = 36,41 seconden.

Er is dan een verschil van  36,41 - 36,37 = 0,04 seconden
       
  c. 40 seconden voor 400 meter is 400/40 = 10 meter per seconde
Dus het aantal meter is het aantal seconden keer 10.
       
  d. Y1 = 11X - 0,0000015X^3 
Y2 = 10X
intersect geeft t = 816,5 seconden
       
  e. s' (816,5) = 11 - 0,0000045 • 816,52 = 8  m/sec
de andere schaatser reed 10 m/sec, dus het snelheidsverschil is 2 m/sec.
       
7. a. B(t) = (8 - 0,1t)3
= (8 - 0,1t)(8 - 0,1t)(8 - 0,1t)
= (64 - 0,8t - 0,8t + 0,01t2)(8 - 0,1t)
= (64 - 1,6t + 0,01t2)(8 - 0,1t)
= 512 - 6,4t -12,8t + 0,16t2 + 0,08t2 - 0,001t3
= 512 - 19,2t + 0,24t2 - 0,001t3
       
  b. B' = -19,2 + 2 • 0,24t - 3 • 0,001t2  =  -19,2 + 0,48t - 0,003t2
De grafiek van B' is een bergparabool die vanaf t = 0 onder de x-as ligt en stijgt.
Dat de grafiek onder de x-as ligt betekent dat de hoeveelheid in het vat afneemt.
Dat de grafiek stijgt betekent dat de snelheid waarmee de hoeveelheid afneemt kleiner wordt (dichter naar nul gaat)
       
  c. B'(0) = -19,2
Dus op t = 0 stroomt het vat leeg met 19,2 liter per minuut.
De vrienden moeten op t = 0 dus 19,2 liter per minuut opdrinken!
Dat gaat niet lukken.....
       
  d. B' = -7,5
-19,2 + 0,48t - 0,003t2  = -7,5
-0,003t2 + 0,48t - 11,7 = 0
ABC-formule:  t = (-0,48 ±√(0,2304 - 0,1404))/-0,006 = 30  (of 130, maar dan is B allang nul) 
       
8. a. L(t) = 0,05t2
L' = 2 • 0,05t = 0,10t
L'(5) = 0,10 • 5 = 0,5 cm/week		  
       
  b. L'(16) = 0,10 • 16 = 1,6  dus  a = 1,6
L(16) = 0,05 • 162 = 12,8
12,8 = 1,6 • 16 + b  ⇒  b = -12,8		  
       
9. a. f(x) = -1/2x2 + 2x + 1.
f ' = 2 • -1/2x + 2 = -x + 2  en dat is de rode lijn hiernaast.

Spiegelen in x= 3 geeft de blauwe lijn.
Die heeft vergelijking  y = x - 4
     
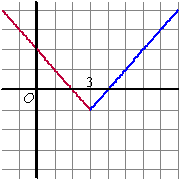  b. f(x) = ax2 + bx + c
f ' = 2ax + b  en dat moet gelijk zijn aan x - 4
dus 2a = 1 ⇒  a = 1/2  en  b = -4

f(3) = -1/2•32 + 2 • 3 + 1 = 21/2
1/2 • 32 - 4 • 3 + c = 21/2
-71/2  + c = 21/2
c = 10
       
10. a. Het vat is leeg  als  h(t) = 0  dus als  0,0008t2 - 0,32t + 32 = 0
De ABC-formule geeft dat dat zo is voor t = 200
De snelheid is de afgeleide en die is gelijk aan  h '(t) = 0,0016t - 0,32
Op t = 200 geldt:  h'(200) = 0 dus is inderdaad op dat moment de snelheid nul.
       
  b. Bij het leegpompen verdwijnt er constant 60 liter per minuut uit de tank.
Bij een inhoud van 60 liter geldt πr2h = 60  met  r = 8,9206... (vraag 1)  dus  h =  0,24  dm/minuut
Bij het leegstromen is de helling  h '(t) = 0,0016t - 0,32.
De hellingen zijn gelijk als  0,0016t - 0,32 = - 0,24  ofwel als t = 50 minuten.
Tussen  t = 0  en  t = 50 loopt de tank bij stromen sneller leeg dan bij pompen.
       
       

© h.hofstede (h.hofstede@hogeland.nl)