© h.hofstede (h.hofstede@hogeland.nl)

       
1. a. de dikte is 2mm en dat is  0,02 dm  (we rekenen alles in dm vanwege de liters)
de inhoud is dan de inhoud van een cilinder:  πr2 • h  = πr2 • 0,02
Dat moet gelijk zijn aan 50t
 πr2 • 0,02 = 50t 
0,0628r2 = 50t
r2 = 50/0,0628 • t  = 795,77 • t
r = √(795,77t) = 28,2√t
Dat is in decimeters, dus het aantal meters is  r = 2,82√t
       
  b. Y1 = 2,82*√(X)
cacl - dy/dx en dan x = 20  geeft  helling 0,315
De vlek groeit dus op dat moment met 0,315 m/min
       
2. a. 0,2 liter = 0,2 dm3 = 200 cm3
dus op tijdstip t is er 200t  cm3 in de ballon geblazen.
4/3πr3 = 200t
   
    De diameter is dan het dubbele daarvan.
       
  b. Y1 = 2 • (150X/π)^(1/3)
calc - dy/dx  en dan X = 2 geeft  helling
       
3. a. Y1 = 2X^3 - 10X^2 + 6X - 4
calc - dy/dx  en dan X = 2 geeft helling  -10.
Dat is negatief, dus x wordt kleiner, dus het punt beweegt naar links.
       
  b. Het punt staat stil als de snelheid (dus de afgeleide) nul is.
Y1 = 2X^3 - 10X^2 + 6X - 4
Y2 = nDeriv(Y1, X, X)
calc - zero van Y2 geeft  t = 0,33  of  t = 3
       
  c. In de oorsprong is x = 0
Y1 = 2X^3 - 10X^2 + 6X - 4
calc - zero  geeft  x = 4,424
cacl - dy/dx en dan X = 4,424 geeft helling (dus snelheid) 34,9  
       
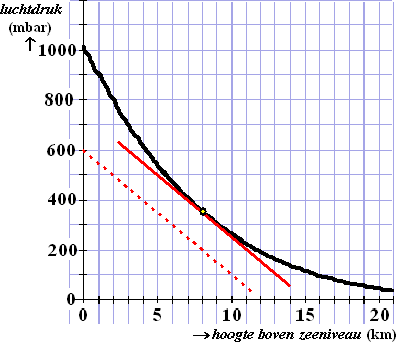
4. a. Teken een willekeurige lijn met helling -5. De rode stippellijn hiernaast.

Verschuif die totdat hij de grafiek raakt.
Dat is de rode lijn hiernaast, en die raakt de grafiek bij x ≈ 8
     
  b. Y1 = 1014 • (-0,0226 • X + 1)^5,26
calc - dy/dx en dan X = 3 geeft helling -89,4
       
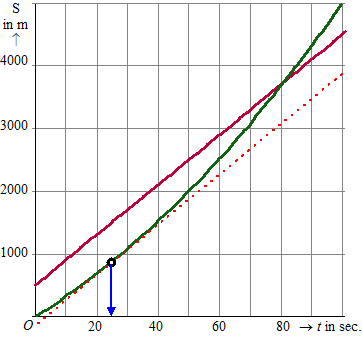
5. a. De helling is 40, dus 40 meter per seconde
Dat is in één uur  3600 • 40 = 144000 meter, dus  144 km/uur.
       
  b. Dan moet de helling van de politiegrafiek gelijk zijn aan de helling van de rechte lijn.
Zie hiernaast:  ongeveer bij t = 25 sec.

     
  c.
t 0 20 40 60 80 100
S 0 680 1520 2520 3680 5000
ΔS - 680 840 1000 1160 1320
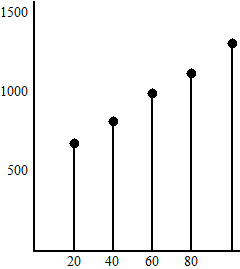
    zie de volgende figuur.
   
       
  d. Y1 = 0,2X^2 + 30X
Y2 = 40X + 500
Intersect geeft  t = 80,90 sec.
       
6. a. V = 0  geeft  8000 • (1 - t/270)2 = 0
Dan is t = 270 minuten
       
  b. Y1 = 8000 • (1 - X/270)^2
calc - dy/dx bij X = 30 geeft -52,67  liter per minuut
dat is 0,88 liter per seconde 
       
7. a.

V(0) = 8000 en V(75) = 4613,54
 DV/Dt = (8000 - 45613,54)/(0 - 75) = 45,15?
Dat betekent dat er op t = 75 gemiddeld  45,15 liter per minuut uit het vat is gestroomd.
       
  b.

Teken een lijn vanaf (0, 8000) met helling -50   ?
Die snijdt de grafiek bij t = 60   
Op dat moment zit er 5000 liter in het vat. 

       
  c.

Teken de raaklijn aan de grafiek bij t = 120  ?
 Bepaal de helling daarvan met  twee punten.
Dat is ongeveer -19,3 

       
  d. calc- dy/dx geeft  -15,79 liter/minuut
       
  e.

zonder pomp:
 ?V = 0  geeft  8300 - 300√(2t + 1) = 0 
300√(2t + 1) = 8300
√(2t + 1) = 27,67
2t + 1 = 765,44
t = 382,22 = 22933 seconden

met pomp:
V(180) = 2600
dat duurt nog 2600/16 = 162,50 minuten  ?
het vat is leeg op  t = 342,50 = 20550 seconden

De winst is  2383 seconden en dat is 39 minuten en 43 seconden. minuten

       
       

© h.hofstede (h.hofstede@hogeland.nl)